2021届高三数学二轮复习微专题——求解圆锥曲线的轨迹方程课件(共22张PPT)
文档属性
| 名称 | 2021届高三数学二轮复习微专题——求解圆锥曲线的轨迹方程课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 11:14:33 | ||
图片预览








文档简介
(共22张PPT)
“定义法”
求圆锥曲线的轨迹方程
2021届高三数学二轮复习微专题
用一个平面去截两个圆锥面,得到的交线
几何图形
代数问题
四种圆锥曲线的由来:
坐
标
系
定
义
一.考纲展示
二.知识回顾
三.方法探究
四.典例精讲
五.巩固提升
六.课后作业
一.考纲展示
一.考纲展示
1、了解圆锥曲线的实际背景,了解圆锥曲线在刻画现实世界和解决实际问题
中的作用
2、掌握椭圆、抛物线的定义、几何图形、标准方程及简单几何性质(范围、
对称性、
顶点、离心率)
3、了解双曲线的定义、几何图形和标准方程,知道它的简单几何性质(范围、
对称性、顶点、离心率)
4、了解曲线与方程的对应关系
5、理解数形结合的思想
6、了解圆锥曲线的简单应用
二.知识回顾
椭圆:
距离之和
距离之差
的绝对值
双曲线:
相等
抛物线:
二.知识回顾
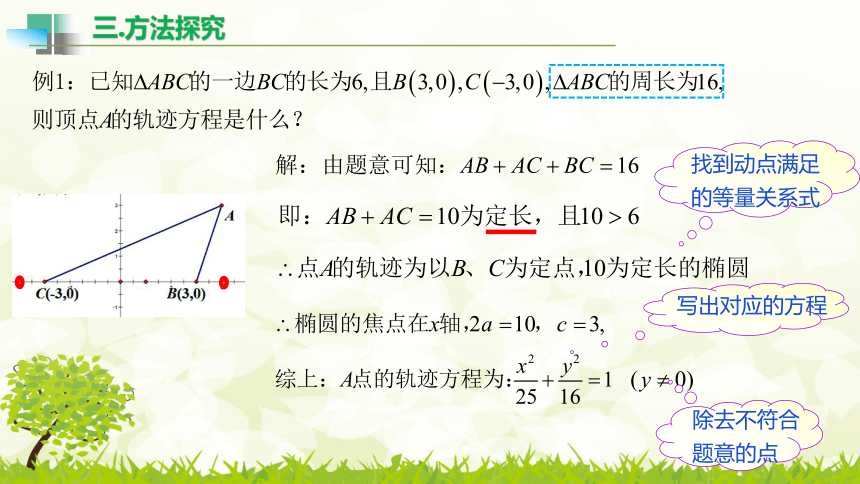
三.方法探究
三.方法探究
找到动点满足
的等量关系式
写出对应的方程
除去不符合
题意的点
(1)定曲线:
(2)定方程:
(3)定范围:
1
3
2
“定义法”求解圆锥曲线轨迹方程的一般步骤:
四.典例精讲
分析:
四.典例精讲
一、定曲线
二、定方程
三、定范围
关键步骤:
1.通过几何图形找到关于动点的等量关系式
2.通过等量关系式找到对应“定义”的曲线
M
Y
X
x
y
外切
外切
内切
内切
内切
外切
外切
内切
两圆的位置关系:
关键在于找圆心距
Y
X
x
y
M
M
M
Y
X
x
y
一、定曲线
二、定方程
M
Y
X
x
y
三、定范围
五.课堂小结
五、课堂小结
定曲线
定方程
定范围
排除不符合题意
的点的范围
根据等量关系式
找到所对应的图形的标准方程
找到动点满足的等量关系式
1、动点到两个定点距离之和为定值——椭圆
2、动点到两个定点距离之差为定值——双曲线
3、动点到定点和定直线距离相等——抛物线
“定义法”求解圆锥曲线轨迹方程的一般步骤:
数形结合
逻辑推理
转化化归
六.课后作业
六、课后作业
一、回顾复习
对本节课的定义法求轨迹方程的步骤、方法进行归纳整理
二、真题训练
1.已知
,
,动圆P与圆M外切且与圆N内切,圆心P轨迹为曲线C,求圆C的方程。
2.已知动圆与
和
都外切,求动圆圆心P轨迹方程。
谢谢!
“定义法”
求圆锥曲线的轨迹方程
2021届高三数学二轮复习微专题
用一个平面去截两个圆锥面,得到的交线
几何图形
代数问题
四种圆锥曲线的由来:
坐
标
系
定
义
一.考纲展示
二.知识回顾
三.方法探究
四.典例精讲
五.巩固提升
六.课后作业
一.考纲展示
一.考纲展示
1、了解圆锥曲线的实际背景,了解圆锥曲线在刻画现实世界和解决实际问题
中的作用
2、掌握椭圆、抛物线的定义、几何图形、标准方程及简单几何性质(范围、
对称性、
顶点、离心率)
3、了解双曲线的定义、几何图形和标准方程,知道它的简单几何性质(范围、
对称性、顶点、离心率)
4、了解曲线与方程的对应关系
5、理解数形结合的思想
6、了解圆锥曲线的简单应用
二.知识回顾
椭圆:
距离之和
距离之差
的绝对值
双曲线:
相等
抛物线:
二.知识回顾
三.方法探究
三.方法探究
找到动点满足
的等量关系式
写出对应的方程
除去不符合
题意的点
(1)定曲线:
(2)定方程:
(3)定范围:
1
3
2
“定义法”求解圆锥曲线轨迹方程的一般步骤:
四.典例精讲
分析:
四.典例精讲
一、定曲线
二、定方程
三、定范围
关键步骤:
1.通过几何图形找到关于动点的等量关系式
2.通过等量关系式找到对应“定义”的曲线
M
Y
X
x
y
外切
外切
内切
内切
内切
外切
外切
内切
两圆的位置关系:
关键在于找圆心距
Y
X
x
y
M
M
M
Y
X
x
y
一、定曲线
二、定方程
M
Y
X
x
y
三、定范围
五.课堂小结
五、课堂小结
定曲线
定方程
定范围
排除不符合题意
的点的范围
根据等量关系式
找到所对应的图形的标准方程
找到动点满足的等量关系式
1、动点到两个定点距离之和为定值——椭圆
2、动点到两个定点距离之差为定值——双曲线
3、动点到定点和定直线距离相等——抛物线
“定义法”求解圆锥曲线轨迹方程的一般步骤:
数形结合
逻辑推理
转化化归
六.课后作业
六、课后作业
一、回顾复习
对本节课的定义法求轨迹方程的步骤、方法进行归纳整理
二、真题训练
1.已知
,
,动圆P与圆M外切且与圆N内切,圆心P轨迹为曲线C,求圆C的方程。
2.已知动圆与
和
都外切,求动圆圆心P轨迹方程。
谢谢!
同课章节目录
