2021-2022学年北师大版八年级数学上册1.1.2 验证勾股定理及简单应用能力提升卷(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学上册1.1.2 验证勾股定理及简单应用能力提升卷(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 200.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-21 09:19:01 | ||
图片预览

文档简介
北师大版八年级数学上册
1.1.2验证勾股定理及简单应用
能力提升卷
一、选择题(共8小题,4
8=32)
1.用四个边长均为a,b,c的直角三角板,拼成如图所示的图形.则下列结论中正确的是(
)
A.
c2=a2+b2
B.c2=a2+2ab+b2
C.c2=a2-2ab+b2
D.c2=(a+b)2
2.勾股定理的验证方法很多,用面积(拼图)证明是最常见的一种方法.如图所示,一个直立的长方体在桌面上慢慢地倒下,启发人们想到勾股定理的证明方法,设AB=c,BC=a,AC=b,证明中用到的面积相等关系是(
)
A.
S△ABC+S△ABD=
S△AFG+S△AEF
B.
S梯形BCEF=S△ABC+S△ABF+S△AEF
C.
S△BDH=S△FGH
D.
S梯形BCEF=S△ABC+S△ABF+S△AEF+S△FGH
3.如图,湖的两端有A,B两点,从与BA方向成直角的BC方向上的点C测得CA=130
m,CB=120
m,则AB的长为(
)
A.30
m
B.40
m
C.50
m
D.60
m
4.放学后,贝贝和京京从学校分手,分别沿西南方向和东南方向回家,已知两人行走的速度都是40
m/min.贝贝用15
min到家,京京用20
min到家,那么贝贝家与京京家的距离是(
)
A.600
m
B.800
m
C.1000
m
D.无法计算
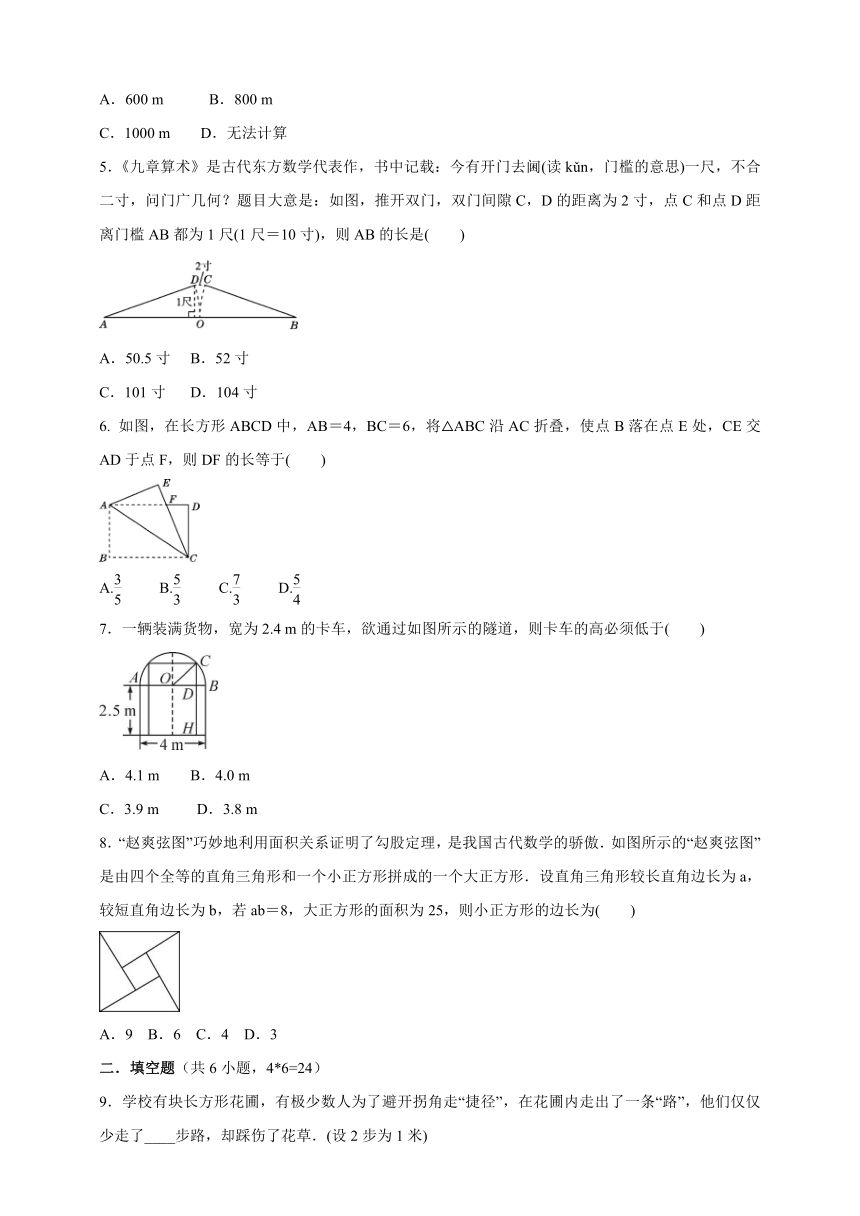
5.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图,推开双门,双门间隙C,D的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是( )
A.50.5寸
B.52寸
C.101寸
D.104寸
6.
如图,在长方形ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )
A.
B.
C.
D.
7.一辆装满货物,宽为2.4
m的卡车,欲通过如图所示的隧道,则卡车的高必须低于(
)
A.4.1
m
B.4.0
m
C.3.9
m
D.3.8
m
8.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为(
)
A.9
B.6
C.4
D.3
二.填空题(共6小题,4
6=24)
9.学校有块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了____步路,却踩伤了花草.(设2步为1米)
10.
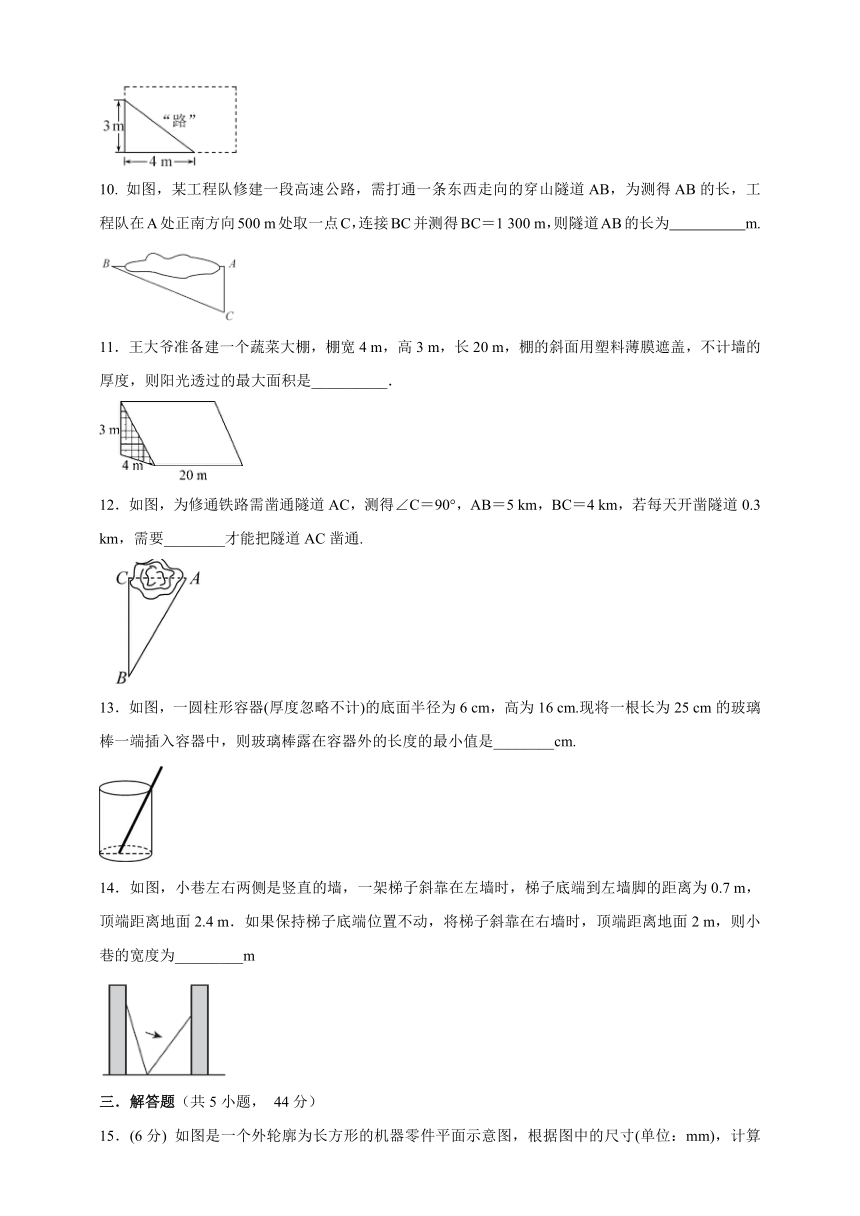
如图,某工程队修建一段高速公路,需打通一条东西走向的穿山隧道AB,为测得AB的长,工程队在A处正南方向500
m处取一点C,连接BC并测得BC=1
300
m,则隧道AB的长为
m.
11.王大爷准备建一个蔬菜大棚,棚宽4
m,高3
m,长20
m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,则阳光透过的最大面积是__________.
12.如图,为修通铁路需凿通隧道AC,测得∠C=90°,AB=5
km,BC=4
km,若每天开凿隧道0.3
km,需要________才能把隧道AC凿通.
13.如图,一圆柱形容器(厚度忽略不计)的底面半径为6
cm,高为16
cm.现将一根长为25
cm的玻璃棒一端插入容器中,则玻璃棒露在容器外的长度的最小值是________cm.
14.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙脚的距离为0.7
m,顶端距离地面2.4
m.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2
m,则小巷的宽度为_________m
三.解答题(共5小题,
44分)
15.(6分)
如图是一个外轮廓为长方形的机器零件平面示意图,根据图中的尺寸(单位:mm),计算出两圆孔中心A和B的距离
16.(8分)
如图,小明从电线杆AB顶牵下长25
m的绳子BC,他用手牵住绳子离地1
m.已知小明距电线杆有24
m(AD),求电线杆的高度AB.
17.(8分)
如图,一个无盖的长方体形盒子的长、宽、高分别为8
cm,8
cm,12
cm,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B,你能帮蚂蚁设计一条最短的线路吗?蚂蚁要爬行的最短路程是多少?
18.(10分)
如图①所示,一个梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,如图②,测得BD长为0.5米,则梯子顶端A下滑了多少米?
19.(12分)
如图,AB为一棵大树,在树上距地面10
m的D处有两只猴子,它们同时发现C处有一筐水果,一只猴子从D处往上爬到树顶A处,又沿滑绳AC到达C处,另一只猴子从D处滑到B处,再由B处跑到C处.已知两只猴子所经过的路程都为15
m,求树高AB.
参考答案
1-4ABCC
5-8CBAD
9.
4
10.
1200
11.
100
m2.
12.
10
13.
5
14.
2.2
15.
解:AC=150-60=90(mm),BC=180-60=120(mm),则AB2=902+1202,所以AB=150
mm.
16.
解:过点C作CE⊥AB于点E,则AE=CD=1
m,CE=AD=24
m.
由勾股定理,得BE2=BC2-CE2=252-242=49,所以BE=7
m.所以AB=7+1=8
(m).
17.
解:由盒子的展开图可知,AB为最短的线路(如图).
由勾股定理,得AB2=(8+8)2+122=400,所以AB=20(cm).即蚂蚁要爬行的最短路程是20
cm.
18.
解:在Rt△ABC中,AC2=AB2-BC2=4,即AC=2米.在Rt△CDE中,CE2=DE2-CD2=2.25,即CE=1.5米,所以AE=2-1.5=0.5(米),即梯子顶端A下滑了0.5米
19.
解:设AD=x
m,则AB=x+10,AC=15-x,在Rt△ABC中,根据勾股定理,得(x+10)2+(15-10)2=(15-x)2,解得x=2,所以AB=12
m.答:树高AB为12
m
1.1.2验证勾股定理及简单应用
能力提升卷
一、选择题(共8小题,4
8=32)
1.用四个边长均为a,b,c的直角三角板,拼成如图所示的图形.则下列结论中正确的是(
)
A.
c2=a2+b2
B.c2=a2+2ab+b2
C.c2=a2-2ab+b2
D.c2=(a+b)2
2.勾股定理的验证方法很多,用面积(拼图)证明是最常见的一种方法.如图所示,一个直立的长方体在桌面上慢慢地倒下,启发人们想到勾股定理的证明方法,设AB=c,BC=a,AC=b,证明中用到的面积相等关系是(
)
A.
S△ABC+S△ABD=
S△AFG+S△AEF
B.
S梯形BCEF=S△ABC+S△ABF+S△AEF
C.
S△BDH=S△FGH
D.
S梯形BCEF=S△ABC+S△ABF+S△AEF+S△FGH
3.如图,湖的两端有A,B两点,从与BA方向成直角的BC方向上的点C测得CA=130
m,CB=120
m,则AB的长为(
)
A.30
m
B.40
m
C.50
m
D.60
m
4.放学后,贝贝和京京从学校分手,分别沿西南方向和东南方向回家,已知两人行走的速度都是40
m/min.贝贝用15
min到家,京京用20
min到家,那么贝贝家与京京家的距离是(
)
A.600
m
B.800
m
C.1000
m
D.无法计算
5.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图,推开双门,双门间隙C,D的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是( )
A.50.5寸
B.52寸
C.101寸
D.104寸
6.
如图,在长方形ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )
A.
B.
C.
D.
7.一辆装满货物,宽为2.4
m的卡车,欲通过如图所示的隧道,则卡车的高必须低于(
)
A.4.1
m
B.4.0
m
C.3.9
m
D.3.8
m
8.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为(
)
A.9
B.6
C.4
D.3
二.填空题(共6小题,4
6=24)
9.学校有块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了____步路,却踩伤了花草.(设2步为1米)
10.
如图,某工程队修建一段高速公路,需打通一条东西走向的穿山隧道AB,为测得AB的长,工程队在A处正南方向500
m处取一点C,连接BC并测得BC=1
300
m,则隧道AB的长为
m.
11.王大爷准备建一个蔬菜大棚,棚宽4
m,高3
m,长20
m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,则阳光透过的最大面积是__________.
12.如图,为修通铁路需凿通隧道AC,测得∠C=90°,AB=5
km,BC=4
km,若每天开凿隧道0.3
km,需要________才能把隧道AC凿通.
13.如图,一圆柱形容器(厚度忽略不计)的底面半径为6
cm,高为16
cm.现将一根长为25
cm的玻璃棒一端插入容器中,则玻璃棒露在容器外的长度的最小值是________cm.
14.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙脚的距离为0.7
m,顶端距离地面2.4
m.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2
m,则小巷的宽度为_________m
三.解答题(共5小题,
44分)
15.(6分)
如图是一个外轮廓为长方形的机器零件平面示意图,根据图中的尺寸(单位:mm),计算出两圆孔中心A和B的距离
16.(8分)
如图,小明从电线杆AB顶牵下长25
m的绳子BC,他用手牵住绳子离地1
m.已知小明距电线杆有24
m(AD),求电线杆的高度AB.
17.(8分)
如图,一个无盖的长方体形盒子的长、宽、高分别为8
cm,8
cm,12
cm,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B,你能帮蚂蚁设计一条最短的线路吗?蚂蚁要爬行的最短路程是多少?
18.(10分)
如图①所示,一个梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,如图②,测得BD长为0.5米,则梯子顶端A下滑了多少米?
19.(12分)
如图,AB为一棵大树,在树上距地面10
m的D处有两只猴子,它们同时发现C处有一筐水果,一只猴子从D处往上爬到树顶A处,又沿滑绳AC到达C处,另一只猴子从D处滑到B处,再由B处跑到C处.已知两只猴子所经过的路程都为15
m,求树高AB.
参考答案
1-4ABCC
5-8CBAD
9.
4
10.
1200
11.
100
m2.
12.
10
13.
5
14.
2.2
15.
解:AC=150-60=90(mm),BC=180-60=120(mm),则AB2=902+1202,所以AB=150
mm.
16.
解:过点C作CE⊥AB于点E,则AE=CD=1
m,CE=AD=24
m.
由勾股定理,得BE2=BC2-CE2=252-242=49,所以BE=7
m.所以AB=7+1=8
(m).
17.
解:由盒子的展开图可知,AB为最短的线路(如图).
由勾股定理,得AB2=(8+8)2+122=400,所以AB=20(cm).即蚂蚁要爬行的最短路程是20
cm.
18.
解:在Rt△ABC中,AC2=AB2-BC2=4,即AC=2米.在Rt△CDE中,CE2=DE2-CD2=2.25,即CE=1.5米,所以AE=2-1.5=0.5(米),即梯子顶端A下滑了0.5米
19.
解:设AD=x
m,则AB=x+10,AC=15-x,在Rt△ABC中,根据勾股定理,得(x+10)2+(15-10)2=(15-x)2,解得x=2,所以AB=12
m.答:树高AB为12
m
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
