2021-2022学年高一上学期数学北师大版(2019)必修第一册 第一章复习专题课件:集合求参类型题归纳(共30张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学北师大版(2019)必修第一册 第一章复习专题课件:集合求参类型题归纳(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 20:10:59 | ||
图片预览










文档简介
(共30张PPT)
课件制作
胡琪
第一章集合复习
北师大(2019)必修1
专题:集合求参类型题归纳
前言
1.利用元素与集合关系及元素的特性求参
2.利用集合与集合的基本关系求参.
3.利用集合与集合的基本运算求参.
环节一
元素与集合关系
已知集合,若,则m的值为(
)
A.1
B.2
C.
D.1或
特点
集合是有限数集,关系是属于
解法
选择能够是3的元素,注意用互异性验算
解
由,可得或,解得或
由集合元素的互异性得?+2≠2?2+?,即?≠±1,所以?=?
设集合A={x|(x-a)2<1},且2∈A,3?A,则实数a的取值范围为________.
特点
①集合是不等式解集;②元素与集合有属于和不属于关系
解法
属于就代入,不属于就代入补集
略解
1集合{x|x2+ax=0}有两个元素0和1.则a的值为________
特点
①一元二次方程解集;②两个元素相当两根
解法
韦达定理
略解
解析:0和1为方程x2+ax=0的两根.
∴0+1=-a,∴a=-1.
环节二
集合与集合关系求参
角度一
有限集关系求参
特点
已知集合A=,B=若B?A,则实数a的取值范围为________.
①含参集合一元一次型方程解集②含参集合是子集
解法
讨论子集空与不空;列举法(不用数轴法)
略解
空集
B=?,a=0,
适合B?A;
非空集
B≠?,a≠0,B=,要使B?A,;
A=
角度二
无限集关系求参
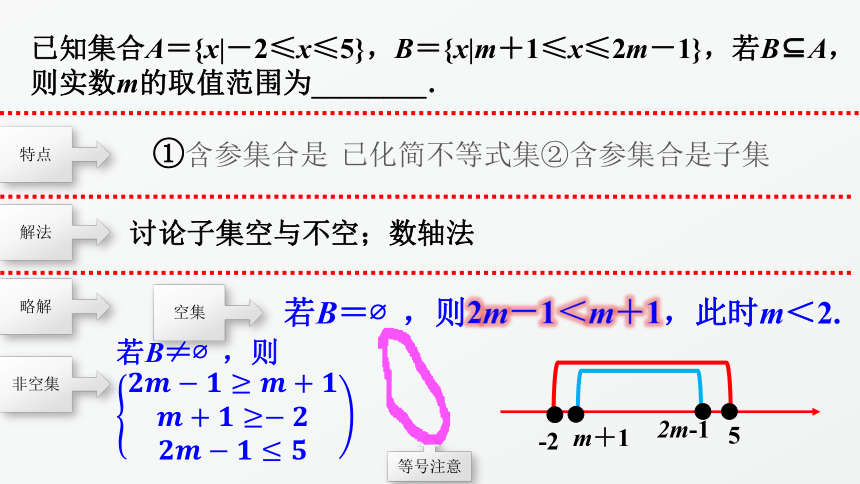
已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},若B?A,则实数m的取值范围为________.
特点
解法
讨论子集空与不空;数轴法
略解
空集
若B=?,则2m-1<m+1,此时m<2.
非空集
若B≠?,则
-2
5
m+1
2m-1
等号注意
①含参集合是
已化简不等式集②含参集合是子集
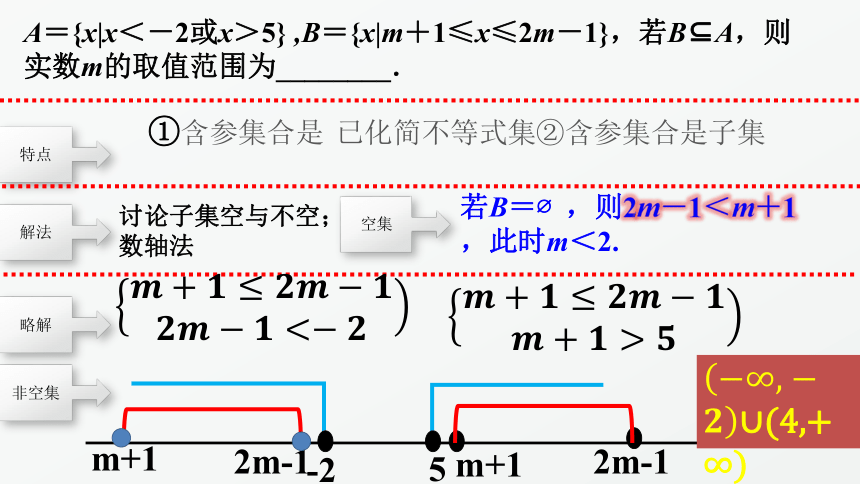
A={x|x<-2或x>5}
,B={x|m+1≤x≤2m-1},若B?A,则实数m的取值范围为________.
特点
①含参集合是
已化简不等式集②含参集合是子集
解法
讨论子集空与不空;数轴法
略解
空集
若B=?,则2m-1<m+1,此时m<2.
非空集
-2
5
m+1
2m-1
m+1
2m-1
∪(4,+∞)
已知集合,集合,集合,若,则实数m的取值范围为
特点
1.含参不等是在大集合,它不会是空集;2.含参一元一次型不等式,解的时候需分类讨论。
解法
求并集,对参数m分三类讨论,最后用数轴处理关系
解
并集
.
分类
①?<0时,集合?={?|?②?=0时,集合?=?,成立.
③?>0时,集合?={?|?>?},∴?≤?1,解得?≤1,∴0.
环节三
集合与集合运算求参
角度一
有限集运算关系求参
已知A={1,2,3,4},B={a+1,2a}.若A∩B={4},
则a=( )
A.3
B.2
C.2或3
D.3或1
特点
集合中元素有限,交集已知
解法
从B集合入手分析,获得参值后,注意验算
解
∵A∩B={4},∴a+1=4或2a=4
验证1
若a+1=4,则a=3,此时B={4,6},符合题意
验证2
若2a=4,则a=2,此时B={3,4},不符合题意
设集合若集合,求实数a的取值范围.
特点
1.集合是一元二次方程根组成的有限集;2.
解法
1.化简A;2.A中元素适合B的补集,不适合B中的方程
解
A
?={1,2}
关系
由?∩(?_?
?)=?,可知?∩?=?
代入
所以,所以
{?|?≠?1,?≠?3,?≠?1+√3,?≠?1?√3}
角度二
无限集运算关系求参
设集合,集合,若,则的取值范围是
特点
1.集合是无限数集;2.
解法
求补集,用数轴实现题目中集合关系
解
集合∴
∵集合且
2
4
a
设全集,集合或,集合.若,则实数n的取值范围为_________;实数m的取值范围为________.
特点
1.集合是化简过的无限数集;2.集合关系是
3.两个参数
解法
数轴分析,一举双得
解
2
4
≥4
{?∣???}
已知集合A=,N=
,A∪N=R,求实数a的取值范围。
特点
集合是无限集,不等式解集,集合关系是A∪N=R
解法
补集
N=
关系
A∪N=
R
1.N的补集,利用数轴体现A∪N=R或A∪N=R,不用求N的补集,直接用数轴研究包含关系
解
结论
3
4
a
a+2
已知集合A=,a取值范围.
特点
1.一个集合是无限数集,一个是二次函数值域;2.
解法
1.解一元二次不等式;求二次函数值域(比较基础);2.数轴分析此题中,A,B都不会是空集)
解
解A
A={?│?2?3?+2≤0}=
解B
x=1
B=
2
a-1
已知集合A=,B=,,求m取值范围
特点
1.两个集合都是无限数集;2.,B集合可以是空集。这与上题不一样。
解法
对B分空与不空,直接用数轴分析
解
空
B=?
非空
不可能
R
角度三
有限集运算关系转包含关系求参
设集合若,求实数a的取值范围;
特点
1.集合由二次方程的根组成的有限集;2.
解法
1.A化简;2.B先不化简,通过包含关系逆向分析;3.要把集合空与不空与一元二次方程根的判别相结合
解
A
知
关系
?∪?=?????
空
当集合时,关于x的方程没有实
数根,所以,即,解得.
不空
一解
两解
达
当集合时,若集合B中只有一个元素,
则,
整理得,解得,
此时,符合题意;
若集合B中有两个元素,则,
综上,可知实数a的取值范围为.
角度三
无限集运算关系转包含关系求参
已知集合A=B=,且则实数的取值范围为
特点
①两个集合都是无限数集②集合运算关系转包含关系)
化简A
得即
A=
化简关系
?∩?=?,则???
空
当时,,
非空
当时,,
已知全集,集合,,若,求实数a的取值范围.
特点
1.集合是无限不等式解集;2.
A
解法
化简集合A,用数轴处理集合包含关系,分空与不空
解
求A
由,解得或,故,
求A补
?_?
?={?1关系
因为,所以.
空
若?=?,即2??1≥1,即?≥1,符合题意;
若?≠?,即?<1,因为??
?,所以2??1≥?1,所以0≤?<1.
不空
谢谢观看
课件制作
胡琪
第一章集合复习
北师大(2019)必修1
专题:集合求参类型题归纳
前言
1.利用元素与集合关系及元素的特性求参
2.利用集合与集合的基本关系求参.
3.利用集合与集合的基本运算求参.
环节一
元素与集合关系
已知集合,若,则m的值为(
)
A.1
B.2
C.
D.1或
特点
集合是有限数集,关系是属于
解法
选择能够是3的元素,注意用互异性验算
解
由,可得或,解得或
由集合元素的互异性得?+2≠2?2+?,即?≠±1,所以?=?
设集合A={x|(x-a)2<1},且2∈A,3?A,则实数a的取值范围为________.
特点
①集合是不等式解集;②元素与集合有属于和不属于关系
解法
属于就代入,不属于就代入补集
略解
1
特点
①一元二次方程解集;②两个元素相当两根
解法
韦达定理
略解
解析:0和1为方程x2+ax=0的两根.
∴0+1=-a,∴a=-1.
环节二
集合与集合关系求参
角度一
有限集关系求参
特点
已知集合A=,B=若B?A,则实数a的取值范围为________.
①含参集合一元一次型方程解集②含参集合是子集
解法
讨论子集空与不空;列举法(不用数轴法)
略解
空集
B=?,a=0,
适合B?A;
非空集
B≠?,a≠0,B=,要使B?A,;
A=
角度二
无限集关系求参
已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},若B?A,则实数m的取值范围为________.
特点
解法
讨论子集空与不空;数轴法
略解
空集
若B=?,则2m-1<m+1,此时m<2.
非空集
若B≠?,则
-2
5
m+1
2m-1
等号注意
①含参集合是
已化简不等式集②含参集合是子集
A={x|x<-2或x>5}
,B={x|m+1≤x≤2m-1},若B?A,则实数m的取值范围为________.
特点
①含参集合是
已化简不等式集②含参集合是子集
解法
讨论子集空与不空;数轴法
略解
空集
若B=?,则2m-1<m+1,此时m<2.
非空集
-2
5
m+1
2m-1
m+1
2m-1
∪(4,+∞)
已知集合,集合,集合,若,则实数m的取值范围为
特点
1.含参不等是在大集合,它不会是空集;2.含参一元一次型不等式,解的时候需分类讨论。
解法
求并集,对参数m分三类讨论,最后用数轴处理关系
解
并集
.
分类
①?<0时,集合?={?|?②?=0时,集合?=?,成立.
③?>0时,集合?={?|?>?},∴?≤?1,解得?≤1,∴0.
环节三
集合与集合运算求参
角度一
有限集运算关系求参
已知A={1,2,3,4},B={a+1,2a}.若A∩B={4},
则a=( )
A.3
B.2
C.2或3
D.3或1
特点
集合中元素有限,交集已知
解法
从B集合入手分析,获得参值后,注意验算
解
∵A∩B={4},∴a+1=4或2a=4
验证1
若a+1=4,则a=3,此时B={4,6},符合题意
验证2
若2a=4,则a=2,此时B={3,4},不符合题意
设集合若集合,求实数a的取值范围.
特点
1.集合是一元二次方程根组成的有限集;2.
解法
1.化简A;2.A中元素适合B的补集,不适合B中的方程
解
A
?={1,2}
关系
由?∩(?_?
?)=?,可知?∩?=?
代入
所以,所以
{?|?≠?1,?≠?3,?≠?1+√3,?≠?1?√3}
角度二
无限集运算关系求参
设集合,集合,若,则的取值范围是
特点
1.集合是无限数集;2.
解法
求补集,用数轴实现题目中集合关系
解
集合∴
∵集合且
2
4
a
设全集,集合或,集合.若,则实数n的取值范围为_________;实数m的取值范围为________.
特点
1.集合是化简过的无限数集;2.集合关系是
3.两个参数
解法
数轴分析,一举双得
解
2
4
≥4
{?∣???}
已知集合A=,N=
,A∪N=R,求实数a的取值范围。
特点
集合是无限集,不等式解集,集合关系是A∪N=R
解法
补集
N=
关系
A∪N=
R
1.N的补集,利用数轴体现A∪N=R或A∪N=R,不用求N的补集,直接用数轴研究包含关系
解
结论
3
4
a
a+2
已知集合A=,a取值范围.
特点
1.一个集合是无限数集,一个是二次函数值域;2.
解法
1.解一元二次不等式;求二次函数值域(比较基础);2.数轴分析此题中,A,B都不会是空集)
解
解A
A={?│?2?3?+2≤0}=
解B
x=1
B=
2
a-1
已知集合A=,B=,,求m取值范围
特点
1.两个集合都是无限数集;2.,B集合可以是空集。这与上题不一样。
解法
对B分空与不空,直接用数轴分析
解
空
B=?
非空
不可能
R
角度三
有限集运算关系转包含关系求参
设集合若,求实数a的取值范围;
特点
1.集合由二次方程的根组成的有限集;2.
解法
1.A化简;2.B先不化简,通过包含关系逆向分析;3.要把集合空与不空与一元二次方程根的判别相结合
解
A
知
关系
?∪?=?????
空
当集合时,关于x的方程没有实
数根,所以,即,解得.
不空
一解
两解
达
当集合时,若集合B中只有一个元素,
则,
整理得,解得,
此时,符合题意;
若集合B中有两个元素,则,
综上,可知实数a的取值范围为.
角度三
无限集运算关系转包含关系求参
已知集合A=B=,且则实数的取值范围为
特点
①两个集合都是无限数集②集合运算关系转包含关系)
化简A
得即
A=
化简关系
?∩?=?,则???
空
当时,,
非空
当时,,
已知全集,集合,,若,求实数a的取值范围.
特点
1.集合是无限不等式解集;2.
A
解法
化简集合A,用数轴处理集合包含关系,分空与不空
解
求A
由,解得或,故,
求A补
?_?
?={?1关系
因为,所以.
空
若?=?,即2??1≥1,即?≥1,符合题意;
若?≠?,即?<1,因为??
?,所以2??1≥?1,所以0≤?<1.
不空
谢谢观看
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
