广东省龙川一中2011-2012学年高一5月月考数学试题
文档属性
| 名称 | 广东省龙川一中2011-2012学年高一5月月考数学试题 | 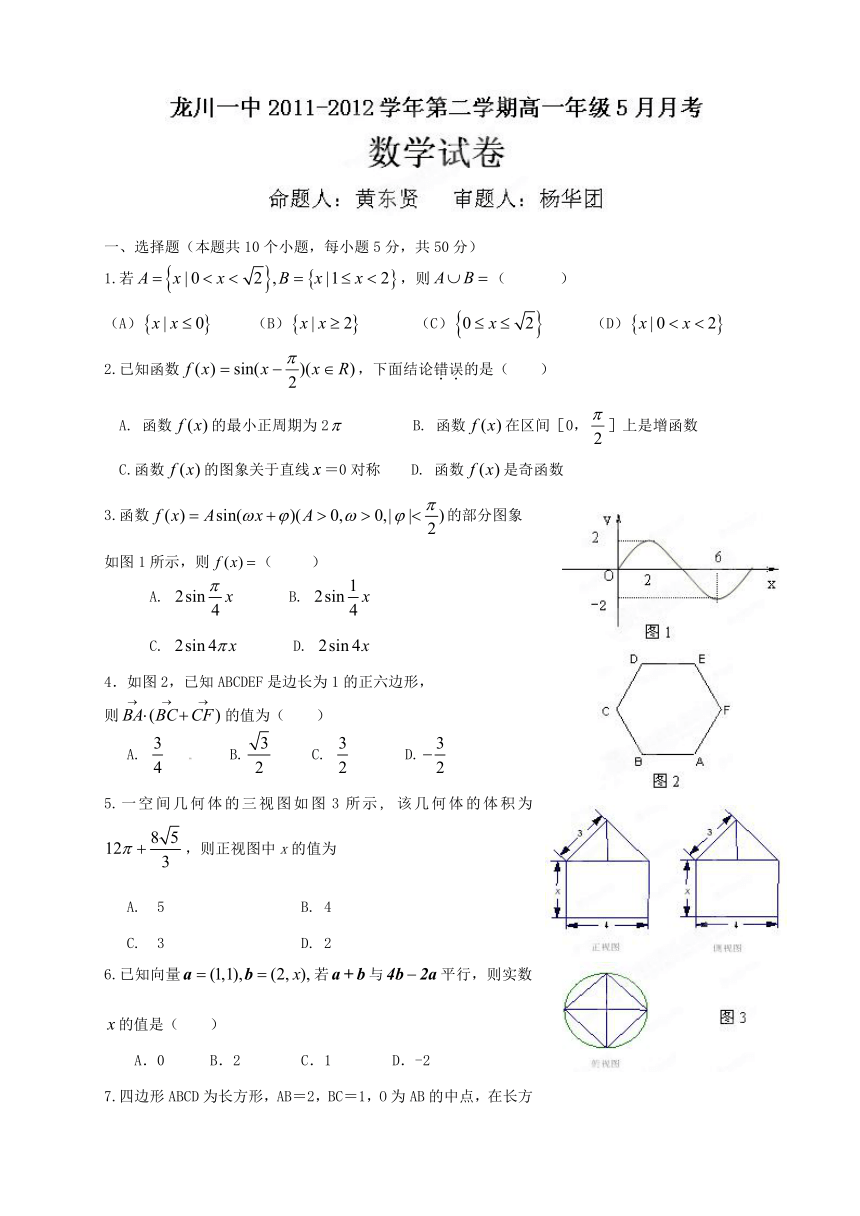 | |
| 格式 | zip | ||
| 文件大小 | 286.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-11 19:38:04 | ||
图片预览



文档简介
一、选择题(本题共10个小题,每小题5分,共50分)
1.若,则( )
(A) (B) (C) (D)
2.已知函数,下面结论错误的是( )
A. 函数的最小正周期为2 B. 函数在区间[0,]上是增函数
C.函数的图象关于直线=0对称 D. 函数是奇函数
3.函数的部分图象
如图1所示,则( )
A. B.
C. D.
4.如图2,已知ABCDEF是边长为1的正六边形,
则的值为( )
A. B. C. D.
5.一空间几何体的三视图如图3所示, 该几何体的体积为,则正视图中x的值为
A. 5 B. 4
C. 3 D. 2
6.已知向量若与平行,则实数的值是( )
A.0 B.2 C.1 D.-2
7.四边形ABCD为长方形,AB=2,BC=1,O为AB的中点,在长方形ABCD内随机取一点,取到的点到O的距离大于1的概率为( )
(A) (B) (C) (D)
8. 将函数y=sinx的图象向左平移0 <2的单位后,得到函数y=sin的图象,则等于( )
A. B. C. D.
9.已知a=(1,-1),b=(λ,1),a与b的夹角为钝角,则λ的取值范围是( )
A.λ>1 B.λ<1 C.λ<-1 D.λ<-1或-1<λ<1
10. 已知函数为偶函数,它在上减函数,若,则x的取值范围是( )A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分)
11.的夹角为, .
12. 已知方向上的投影为 。
13. 已知直线与圆相切,且与直线平行,则直线的方程是 .
14.在平面直角坐标系中,横、纵坐标均为整数的点叫做格点.若函y=f(x)的图像恰好经过k 个格点,则称函数y=f(x)为k阶格点函数.已知函数:①y=2sinx;②y=cos (x+);③;④ .其中为一阶格点函数的序号为 (注:把你认为正确论断的序号都填上)
三、解答题(本题共6小题,共80分。解答应写出文字说明、证明过程或演算步骤)
15. (本小题满分12分)已知函数(其中)的图象与x轴的交点中,相邻两个交点之间的距离为,且图象上一个最低点为.
(1)求的解析式;
(2)当,求的值域.
16. (本小题满分12分) 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图4.()
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
17.(本小题满分14分)
如图①边长为1的正方形ABCD中,点E、F分别
为AB、BC的中点,将△BEF剪去,将
△AED、△DCF分别沿DE、DF折起,使A、
C两点重合于点P得一个三棱锥如图②示.
(1)求证:;
(2)求三棱锥的体积;
(3)求DE与平面PDF所成角的正弦值.
18. (本题满分14分)提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车速度为0;当车流密度不超过20辆/千米时,车流速度为60千米,/小时,研究表明:当时,车流速度v是车流密度的一次函数.
(Ⅰ)当时,求函数的表达式;
(Ⅱ)当车流密度为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)可以达到最大,并求出最大值.(精确到1辆/小时)
19.(本题满分14分)已知圆,圆,动点到圆,上点的距离的最小值相等.
(1)求点的轨迹方程;
(2)点的轨迹上是否存在点,使得点到点的距离减去点到点的距离的差为,如果存在求出点坐标,如果不存在说明理由.
20.(本题满分14分) 设为实数,函数.(1)若,求的取值范围;(2)求的最小值;(3)设函数,直接写出(不需给出演算步骤)不等式的解集.
龙川一中2011-2012学年第二学期高一年级5月月考
数学参考答案
一、DDACC BBADB
11. 7 12. 13. 或 14. ①③
15.解(1)由最低点为得A=2.
又,∴,于是;
16.解:(1)由茎叶图可知:甲班身高集中于之间,而乙班身高集中于 之间。因此乙班平均身高高于甲班;
(2)
甲班的样本方差为
=57
17.(1)证明:依题意知图①折前,∴,
∵ ∴平面又∵平面
∴
(2)解法1:依题意知图①中AE=CF= ∴PE= PF=,在△BEF中,
在中,
∴
∴.
【(2)解法2:依题意知图①中AE=CF= ∴PE= PF=,
在△BEF中,
取EF的中点M,连结PM
则,∴
∴
∴.
18.解:(Ⅰ)由题意:当时,;当时,设
再由已知得,解得
故函数的表达式为
(Ⅱ)依题意并由(Ⅰ)可得
当时,为增函数,故当时,其最大值为60×20=1200;
当时,
所以,当时,在区间[20,200]上取得最大值.
综上,当时,在区间[0,200]上取得最大值.
即当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时.
(2)假设这样的点存在,设点
因为点到点的距离减去点到点的距离的差为4,
所以,
,
20.解: (1)若,则
(2)当时,
当时,
综上
(3)时,得,
当时,;
当时,△>0,得:
讨论得:当时,解集为;
当时,解集为;
当时,解集为.
1.若,则( )
(A) (B) (C) (D)
2.已知函数,下面结论错误的是( )
A. 函数的最小正周期为2 B. 函数在区间[0,]上是增函数
C.函数的图象关于直线=0对称 D. 函数是奇函数
3.函数的部分图象
如图1所示,则( )
A. B.
C. D.
4.如图2,已知ABCDEF是边长为1的正六边形,
则的值为( )
A. B. C. D.
5.一空间几何体的三视图如图3所示, 该几何体的体积为,则正视图中x的值为
A. 5 B. 4
C. 3 D. 2
6.已知向量若与平行,则实数的值是( )
A.0 B.2 C.1 D.-2
7.四边形ABCD为长方形,AB=2,BC=1,O为AB的中点,在长方形ABCD内随机取一点,取到的点到O的距离大于1的概率为( )
(A) (B) (C) (D)
8. 将函数y=sinx的图象向左平移0 <2的单位后,得到函数y=sin的图象,则等于( )
A. B. C. D.
9.已知a=(1,-1),b=(λ,1),a与b的夹角为钝角,则λ的取值范围是( )
A.λ>1 B.λ<1 C.λ<-1 D.λ<-1或-1<λ<1
10. 已知函数为偶函数,它在上减函数,若,则x的取值范围是( )A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分)
11.的夹角为, .
12. 已知方向上的投影为 。
13. 已知直线与圆相切,且与直线平行,则直线的方程是 .
14.在平面直角坐标系中,横、纵坐标均为整数的点叫做格点.若函y=f(x)的图像恰好经过k 个格点,则称函数y=f(x)为k阶格点函数.已知函数:①y=2sinx;②y=cos (x+);③;④ .其中为一阶格点函数的序号为 (注:把你认为正确论断的序号都填上)
三、解答题(本题共6小题,共80分。解答应写出文字说明、证明过程或演算步骤)
15. (本小题满分12分)已知函数(其中)的图象与x轴的交点中,相邻两个交点之间的距离为,且图象上一个最低点为.
(1)求的解析式;
(2)当,求的值域.
16. (本小题满分12分) 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图4.()
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
17.(本小题满分14分)
如图①边长为1的正方形ABCD中,点E、F分别
为AB、BC的中点,将△BEF剪去,将
△AED、△DCF分别沿DE、DF折起,使A、
C两点重合于点P得一个三棱锥如图②示.
(1)求证:;
(2)求三棱锥的体积;
(3)求DE与平面PDF所成角的正弦值.
18. (本题满分14分)提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车速度为0;当车流密度不超过20辆/千米时,车流速度为60千米,/小时,研究表明:当时,车流速度v是车流密度的一次函数.
(Ⅰ)当时,求函数的表达式;
(Ⅱ)当车流密度为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)可以达到最大,并求出最大值.(精确到1辆/小时)
19.(本题满分14分)已知圆,圆,动点到圆,上点的距离的最小值相等.
(1)求点的轨迹方程;
(2)点的轨迹上是否存在点,使得点到点的距离减去点到点的距离的差为,如果存在求出点坐标,如果不存在说明理由.
20.(本题满分14分) 设为实数,函数.(1)若,求的取值范围;(2)求的最小值;(3)设函数,直接写出(不需给出演算步骤)不等式的解集.
龙川一中2011-2012学年第二学期高一年级5月月考
数学参考答案
一、DDACC BBADB
11. 7 12. 13. 或 14. ①③
15.解(1)由最低点为得A=2.
又,∴,于是;
16.解:(1)由茎叶图可知:甲班身高集中于之间,而乙班身高集中于 之间。因此乙班平均身高高于甲班;
(2)
甲班的样本方差为
=57
17.(1)证明:依题意知图①折前,∴,
∵ ∴平面又∵平面
∴
(2)解法1:依题意知图①中AE=CF= ∴PE= PF=,在△BEF中,
在中,
∴
∴.
【(2)解法2:依题意知图①中AE=CF= ∴PE= PF=,
在△BEF中,
取EF的中点M,连结PM
则,∴
∴
∴.
18.解:(Ⅰ)由题意:当时,;当时,设
再由已知得,解得
故函数的表达式为
(Ⅱ)依题意并由(Ⅰ)可得
当时,为增函数,故当时,其最大值为60×20=1200;
当时,
所以,当时,在区间[20,200]上取得最大值.
综上,当时,在区间[0,200]上取得最大值.
即当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时.
(2)假设这样的点存在,设点
因为点到点的距离减去点到点的距离的差为4,
所以,
,
20.解: (1)若,则
(2)当时,
当时,
综上
(3)时,得,
当时,;
当时,△>0,得:
讨论得:当时,解集为;
当时,解集为;
当时,解集为.
同课章节目录
