1.1.2 验证勾股定理及简单应用同步练习题 2021-2022学年北师大版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 1.1.2 验证勾股定理及简单应用同步练习题 2021-2022学年北师大版八年级数学上册(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 252.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 14:44:05 | ||
图片预览



文档简介
1.1.2
验证勾股定理及简单应用
一、选择题(共8小题,4
8=32)
1.历史上对勾股定理的一种证法采用了下列图形:其中两个全等的直角三角形边AE、EB在一条直线上.证明中用到的面积相等关系是( )
A.S△EDA=S△CEB
B.S△EDA+S△CEB=S△CDE
C.S四边形CDAE=S四边形CDEB
D.S△EDA+S△CDE+S△CEB=S四边形ABCD
2.勾股定理是“人类最伟大的十个科学发现之一”.我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是( )
A.
B.
C.
D.
3.为迎接新年的到来,同学们做了许多拉花布置教室,准备召开新年晚会,小刘搬来一架高2.5米的木梯,准备把拉花挂到2.4米高的墙上,则梯脚与墙角距离应为( )
A.0.7米
B.0.8米
C.0.9米
D.1.0米
4.如图,要建一个一面靠墙的西红柿大棚,棚宽a=4m,墙高b=3m,棚长d=12m,则覆盖在顶上的塑料薄膜需要的面积至少应为( )
A.36m2
B.48m2
C.60m2
D.84m2
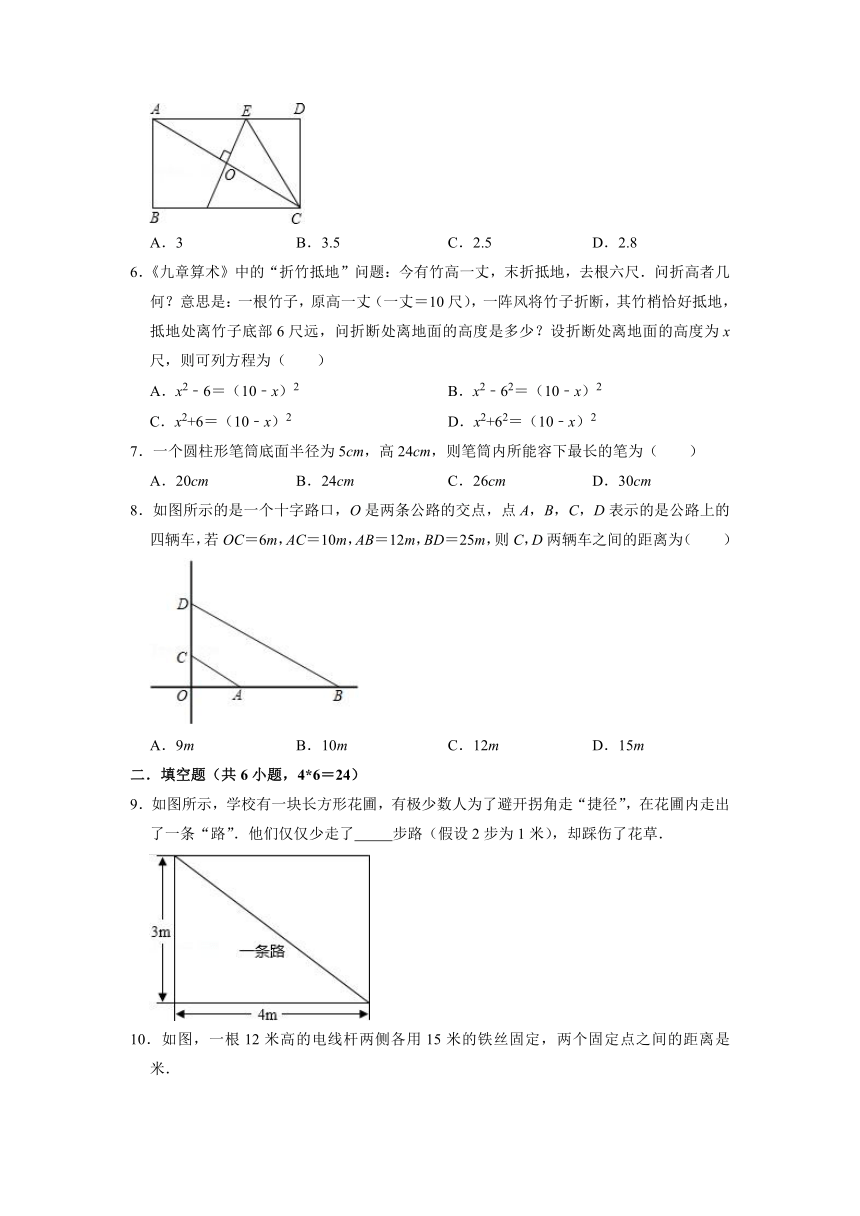
5.如图,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则CE的长为( )
A.3
B.3.5
C.2.5
D.2.8
6.《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A.x2﹣6=(10﹣x)2
B.x2﹣62=(10﹣x)2
C.x2+6=(10﹣x)2
D.x2+62=(10﹣x)2
7.一个圆柱形笔筒底面半径为5cm,高24cm,则笔筒内所能容下最长的笔为( )
A.20cm
B.24cm
C.26cm
D.30cm
8.如图所示的是一个十字路口,O是两条公路的交点,点A,B,C,D表示的是公路上的四辆车,若OC=6m,AC=10m,AB=12m,BD=25m,则C,D两辆车之间的距离为( )
A.9m
B.10m
C.12m
D.15m
二.填空题(共6小题,4
6=24)
9.如图所示,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了
步路(假设2步为1米),却踩伤了花草.
10.如图,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点之间的距离是
米.
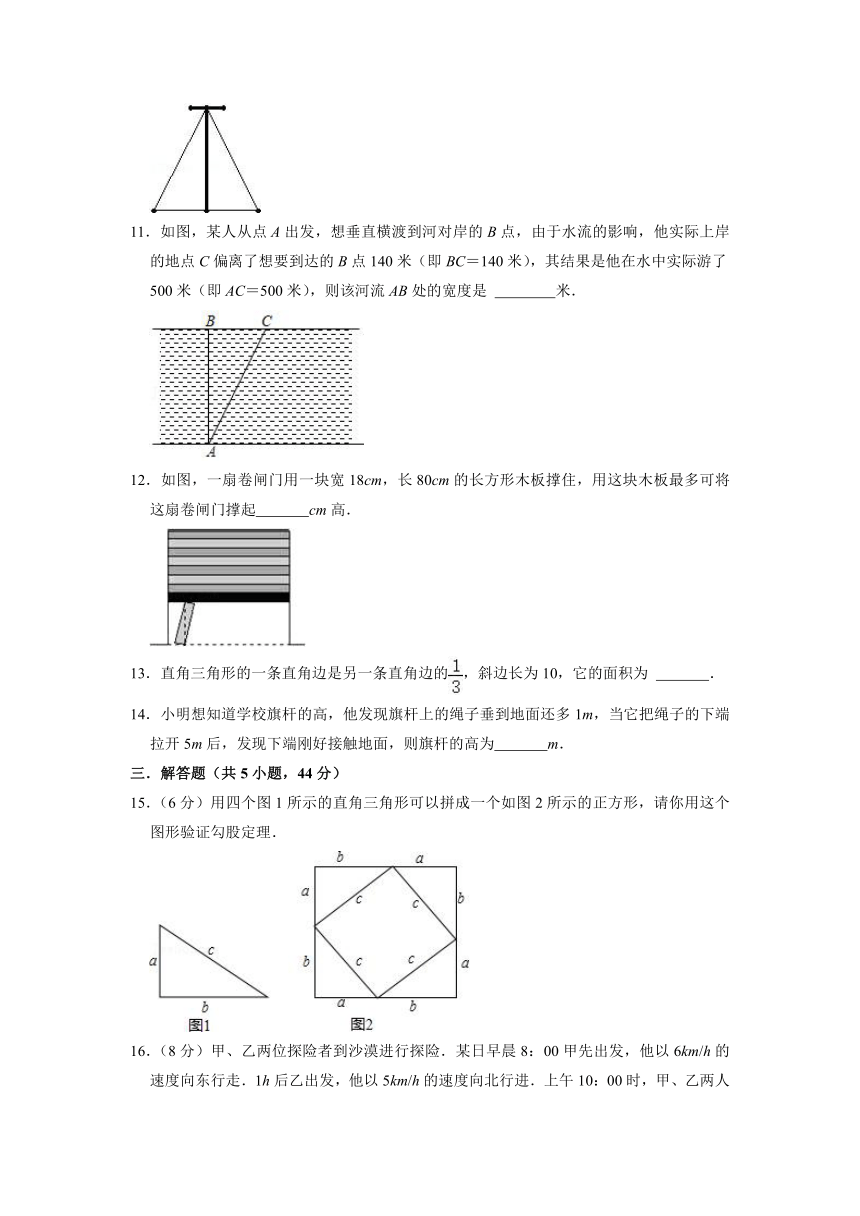
11.如图,某人从点A出发,想垂直横渡到河对岸的B点,由于水流的影响,他实际上岸的地点C偏离了想要到达的B点140米(即BC=140米),其结果是他在水中实际游了500米(即AC=500米),则该河流AB处的宽度是
米.
12.如图,一扇卷闸门用一块宽18cm,长80cm的长方形木板撑住,用这块木板最多可将这扇卷闸门撑起
cm高.
13.直角三角形的一条直角边是另一条直角边的,斜边长为10,它的面积为
.
14.小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多1m,当它把绳子的下端拉开5m后,发现下端刚好接触地面,则旗杆的高为
m.
三.解答题(共5小题,44分)
15.(6分)用四个图1所示的直角三角形可以拼成一个如图2所示的正方形,请你用这个图形验证勾股定理.
16.(8分)甲、乙两位探险者到沙漠进行探险.某日早晨8:00甲先出发,他以6km/h的速度向东行走.1h后乙出发,他以5km/h的速度向北行进.上午10:00时,甲、乙两人相距有多远?
17.(8分)《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图,推开双门,双门间隙C,D的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),求AB的长.
18.(10分)如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,顶端距离地面的高度AC为2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面的高度A′D为2米,求小巷的宽度.
19.(12分)在四边形ABCD中,已知AB=AD=8,∠A=60°,∠D=150°,四边形的周长为32,
(1)连接BD,试判断△ABD的形状;
(2)求BC的长.
参考答案与试题解析
一、选择题(共8小题,4
8=32)
1.历史上对勾股定理的一种证法采用了下列图形:其中两个全等的直角三角形边AE、EB在一条直线上.证明中用到的面积相等关系是( )
A.S△EDA=S△CEB
B.S△EDA+S△CEB=S△CDE
C.S四边形CDAE=S四边形CDEB
D.S△EDA+S△CDE+S△CEB=S四边形ABCD
【分析】用三角形的面积和、梯形的面积来表示这个图形的面积,从而证明勾股定理.
【解答】解:∵由S△EDA+S△CDE+S△CEB=S四边形ABCD.
可知ab+c2+ab=(a+b)2,
∴c2+2ab=a2+2ab+b2,整理得a2+b2=c2,
∴证明中用到的面积相等关系是:S△EDA+S△CDE+S△CEB=S四边形ABCD.
故选:D.
2.勾股定理是“人类最伟大的十个科学发现之一”.我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是( )
A.
B.
C.
D.
【分析】“赵爽弦图”是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形.
【解答】解:“赵爽弦图”是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示:
故选:B.
3.为迎接新年的到来,同学们做了许多拉花布置教室,准备召开新年晚会,小刘搬来一架高2.5米的木梯,准备把拉花挂到2.4米高的墙上,则梯脚与墙角距离应为( )
A.0.7米
B.0.8米
C.0.9米
D.1.0米
【分析】仔细分析题意得:梯子、地面、墙刚好形成一直角三角形,梯高为斜边,利用勾股定理解此直角三角形即可.
【解答】解:梯脚与墙角距离:=0.7(米).
故选:A.
4.如图,要建一个一面靠墙的西红柿大棚,棚宽a=4m,墙高b=3m,棚长d=12m,则覆盖在顶上的塑料薄膜需要的面积至少应为( )
A.36m2
B.48m2
C.60m2
D.84m2
【分析】因为b为高,所以△ABC是直角三角形,先根据勾股定理求出AB的长,再根据矩形的面积公式即可求出矩形ABDE的面积,即盖在顶上的塑料薄膜的面积.
【解答】解:∵b⊥a,
∴△ABC是直角三角形,则AB==5(m),
∴S矩形ABDE=AB?d=5×12=60(m2),
故选:C.
5.如图,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则CE的长为( )
A.3
B.3.5
C.2.5
D.2.8
【分析】根据线段垂直平分线上的点到线段两端点的距离相等的性质可得AE=CE,设CE=x,表示出ED的长度,然后在Rt△CDE中,利用勾股定理列式计算即可得解.
【解答】解:∵EO是AC的垂直平分线,
∴AE=CE,
设CE=x,则ED=AD﹣AE=4﹣x,
在Rt△CDE中,CE2=CD2+ED2,
即x2=22+(4﹣x)2,
解得x=2.5,
即CE的长为2.5.
故选:C.
6.《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A.x2﹣6=(10﹣x)2
B.x2﹣62=(10﹣x)2
C.x2+6=(10﹣x)2
D.x2+62=(10﹣x)2
【分析】根据题意画出图形,设折断处离地面的高度为x尺,再利用勾股定理列出方程即可.
【解答】解:如图,设折断处离地面的高度为x尺,则AB=10﹣x,BC=6,
在Rt△ABC中,AC2+BC2=AB2,即x2+62=(10﹣x)2.
故选:D.
7.一个圆柱形笔筒底面半径为5cm,高24cm,则笔筒内所能容下最长的笔为( )
A.20cm
B.24cm
C.26cm
D.30cm
【分析】桶内容下的木棒最长时,木棒、圆桶的直径、桶高三者正好构成一个直角三角形,根据勾股定理即可求解.
【解答】解:如图,AC为圆桶底面直径,CB是桶高,
∴AC=2×5=10(cm),CB=24cm,
∴线段AB的长度就是桶内所能容下的最长木棒的长度,
在Rt△ABC中,AC2+BC2=AB2,
AB===26(cm).
故桶内所能容下的最长木棒的长度为26cm.
故选:C.
8.如图所示的是一个十字路口,O是两条公路的交点,点A,B,C,D表示的是公路上的四辆车,若OC=6m,AC=10m,AB=12m,BD=25m,则C,D两辆车之间的距离为( )
A.9m
B.10m
C.12m
D.15m
【分析】在Rt△AOC中根据勾股定理求出OA的长,进而可得OB,在Rt△BOD中根据勾股定理可得OD的长,可得答案.
【解答】解:在Rt△AOC中,∵OA2+OC2=AC2,
∴OA=(m),
∴OB=OA+AB=20m,
在Rt△BOD中,∵BD2=OB2+OD2,
∴OD=(m),
∴CD=OD﹣OC=9m,
故选:A.
二.填空题(共6小题,4
6=24)
9.如图所示,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了 4 步路(假设2步为1米),却踩伤了花草.
【分析】本题关键是求出路长,即三角形的斜边长.求两直角边的和与斜边的差.
【解答】解:根据勾股定理可得斜边长是=5m.
则少走的距离是3+4﹣5=2m,
∵2步为1米,
∴少走了4步,
故答案为:4.
10.如图,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点之间的距离是 18 米.
【分析】运用勾股定理可将三角形的直角边求出,将两个直角边进行相加即为两个固定点之间的距离.
【解答】解:∵电线杆高为12m,铁丝长15m,
∴固定点与电线杆的距离==9m,
∵两个直角三角形全等,
∴两个固定点之间的距离=9×2=18m.
11.如图,某人从点A出发,想垂直横渡到河对岸的B点,由于水流的影响,他实际上岸的地点C偏离了想要到达的B点140米(即BC=140米),其结果是他在水中实际游了500米(即AC=500米),则该河流AB处的宽度是
480 米.
【分析】把实际问题转化为数学模型,构造直角三角形,然后利用勾股定理解决.
【解答】解:在Rt△ABC中,AB2+BC2=AC2,AC=500米,BC=140米,
所以AB===480(米).
答:该河流AB处的宽度为480米.
故答案为:480.
12.如图,一扇卷闸门用一块宽18cm,长80cm的长方形木板撑住,用这块木板最多可将这扇卷闸门撑起 82 cm高.
【分析】将长方形木板的对角线可将卷闸门撑起的最高,可用勾股定理将长方形的对角线的距离求出.
【解答】解:设长方形的长为a,宽为b,对角线的长度为c,
∵a=80cm,b=18cm,
∴c===82cm.
故最多可将这扇卷闸门撑起82cm.
13.直角三角形的一条直角边是另一条直角边的,斜边长为10,它的面积为
15 .
【分析】设一条直角边的长为x,则另一直角边为3x,根据勾股定理即可求出x.由三角形的面积公式可得出答案.
【解答】解:设一条直角边的长为x,则另一直角边为3x,
∵斜边长为10,
∴x2+(3x)2=102,
∴x=,
∴两直角边为,3,
∴直角三角形的面积为×=15.
故答案为15.
14.小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多1m,当它把绳子的下端拉开5m后,发现下端刚好接触地面,则旗杆的高为 12 m.
【分析】根据题意设旗杆的高AB为xm,则绳子AC的长为(x+1)m,再利用勾股定理即可求得AB的长,即旗杆的高.
【解答】解:设旗杆的高AB为xm,则绳子AC的长为(x+1)m.
在Rt△ABC中,AB2+BC2=AC2,
∴x2+52=(x+1)2,
解得x=12,
∴AB=12.
∴旗杆的高12m.
故答案是:12.
三.解答题(共5小题,44分)
15.(6分)用四个图1所示的直角三角形可以拼成一个如图2所示的正方形,请你用这个图形验证勾股定理.
【分析】勾股定理的证明可以通过图形的面积之间的关系来完成.
【解答】证明:∵大正方形的面积表示为(a+b)2,大正方形的面积也可表示为c2+4×ab
∴(a+b)2=c2+4×ab,a2+b2+2ab=c2+2ab,
∴a2+b2=c2,
即直角三角形两直角边的平方和等于斜边的平方.
16.(8分)甲、乙两位探险者到沙漠进行探险.某日早晨8:00甲先出发,他以6km/h的速度向东行走.1h后乙出发,他以5km/h的速度向北行进.上午10:00时,甲、乙两人相距有多远?
【分析】甲、乙行走的路线夹角为90°,根据速度和时间可以求得甲、乙行走的路程,在直角三角形中已知两直角边,根据勾股定理可以计算斜边的长.
【解答】解:甲、乙行走的路线夹角为90°,
则△ABC为直角三角形,∵早晨8:00甲先出发,
上午10:00时,甲行走的时间为:10﹣8=2小时,
∴AB=6×(10﹣8)km=12km,
∵1h后乙出发,乙行走的时间为:10﹣9=1小时,
∴AC=5×(10﹣9)km=5km,
在Rt△ABC中,BC为斜边,
则BC==13km,
答:上午10点,甲、乙两人相距13km.
17.(8分)《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图,推开双门,双门间隙C,D的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),求AB的长.
【分析】取AB的中点O,过D作DE⊥AB于E,根据勾股定理解答即可得到结论.
【解答】解:取AB的中点O,过D作DE⊥AB于E,如图所示,
由题意得OA=OB=AD=BC,DE=1尺=10寸,OE=CD=1寸,
设OA=OB=AD=BC=r寸,则AB=2r寸,AE=(r﹣1)寸.
在Rt△ADE中,AE2+DE2=AD2,
即(r﹣1)2+102=r2,
解得r=50.5.
所以2r=101,
所以AB=101寸.
18.(10分)如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,顶端距离地面的高度AC为2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面的高度A′D为2米,求小巷的宽度.
【分析】先根据勾股定理求出AB的长,同理可得出BD的长,进而可得出结论.
【解答】解:在Rt△ACB中,∵∠ACB=90°,BC=0.7米,AC=2.4米,
∴AB2=0.72+2.42=6.25.
在Rt△A′BD中,∵∠A′DB=90°,A′D=2米,BD2+A′D2=A′B′2,
∴BD2+22=6.25,
∴BD2=2.25.
∵BD>0,
∴BD=1.5米.
∴CD=BC+BD=0.7+1.5=2.2米.
答:小巷的宽度CD为2.2米.
19.(12分)在四边形ABCD中,已知AB=AD=8,∠A=60°,∠D=150°,四边形的周长为32,
(1)连接BD,试判断△ABD的形状;
(2)求BC的长.
【分析】(1)直接利用等边三角形的判定方法分析得出答案;
(2)利用勾股定理求出BC的长.
【解答】解:(1)如图,∵AB=AD=8,∠A=60°,
∴△ABD是等边三角形;
(2)∵∠BDC=150°﹣60°=90°,
∴设BC=x,
由勾股定理可知:x2=(16﹣x)2+82,
解得:x=10,
∴BC=10.
验证勾股定理及简单应用
一、选择题(共8小题,4
8=32)
1.历史上对勾股定理的一种证法采用了下列图形:其中两个全等的直角三角形边AE、EB在一条直线上.证明中用到的面积相等关系是( )
A.S△EDA=S△CEB
B.S△EDA+S△CEB=S△CDE
C.S四边形CDAE=S四边形CDEB
D.S△EDA+S△CDE+S△CEB=S四边形ABCD
2.勾股定理是“人类最伟大的十个科学发现之一”.我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是( )
A.
B.
C.
D.
3.为迎接新年的到来,同学们做了许多拉花布置教室,准备召开新年晚会,小刘搬来一架高2.5米的木梯,准备把拉花挂到2.4米高的墙上,则梯脚与墙角距离应为( )
A.0.7米
B.0.8米
C.0.9米
D.1.0米
4.如图,要建一个一面靠墙的西红柿大棚,棚宽a=4m,墙高b=3m,棚长d=12m,则覆盖在顶上的塑料薄膜需要的面积至少应为( )
A.36m2
B.48m2
C.60m2
D.84m2
5.如图,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则CE的长为( )
A.3
B.3.5
C.2.5
D.2.8
6.《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A.x2﹣6=(10﹣x)2
B.x2﹣62=(10﹣x)2
C.x2+6=(10﹣x)2
D.x2+62=(10﹣x)2
7.一个圆柱形笔筒底面半径为5cm,高24cm,则笔筒内所能容下最长的笔为( )
A.20cm
B.24cm
C.26cm
D.30cm
8.如图所示的是一个十字路口,O是两条公路的交点,点A,B,C,D表示的是公路上的四辆车,若OC=6m,AC=10m,AB=12m,BD=25m,则C,D两辆车之间的距离为( )
A.9m
B.10m
C.12m
D.15m
二.填空题(共6小题,4
6=24)
9.如图所示,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了
步路(假设2步为1米),却踩伤了花草.
10.如图,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点之间的距离是
米.
11.如图,某人从点A出发,想垂直横渡到河对岸的B点,由于水流的影响,他实际上岸的地点C偏离了想要到达的B点140米(即BC=140米),其结果是他在水中实际游了500米(即AC=500米),则该河流AB处的宽度是
米.
12.如图,一扇卷闸门用一块宽18cm,长80cm的长方形木板撑住,用这块木板最多可将这扇卷闸门撑起
cm高.
13.直角三角形的一条直角边是另一条直角边的,斜边长为10,它的面积为
.
14.小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多1m,当它把绳子的下端拉开5m后,发现下端刚好接触地面,则旗杆的高为
m.
三.解答题(共5小题,44分)
15.(6分)用四个图1所示的直角三角形可以拼成一个如图2所示的正方形,请你用这个图形验证勾股定理.
16.(8分)甲、乙两位探险者到沙漠进行探险.某日早晨8:00甲先出发,他以6km/h的速度向东行走.1h后乙出发,他以5km/h的速度向北行进.上午10:00时,甲、乙两人相距有多远?
17.(8分)《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图,推开双门,双门间隙C,D的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),求AB的长.
18.(10分)如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,顶端距离地面的高度AC为2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面的高度A′D为2米,求小巷的宽度.
19.(12分)在四边形ABCD中,已知AB=AD=8,∠A=60°,∠D=150°,四边形的周长为32,
(1)连接BD,试判断△ABD的形状;
(2)求BC的长.
参考答案与试题解析
一、选择题(共8小题,4
8=32)
1.历史上对勾股定理的一种证法采用了下列图形:其中两个全等的直角三角形边AE、EB在一条直线上.证明中用到的面积相等关系是( )
A.S△EDA=S△CEB
B.S△EDA+S△CEB=S△CDE
C.S四边形CDAE=S四边形CDEB
D.S△EDA+S△CDE+S△CEB=S四边形ABCD
【分析】用三角形的面积和、梯形的面积来表示这个图形的面积,从而证明勾股定理.
【解答】解:∵由S△EDA+S△CDE+S△CEB=S四边形ABCD.
可知ab+c2+ab=(a+b)2,
∴c2+2ab=a2+2ab+b2,整理得a2+b2=c2,
∴证明中用到的面积相等关系是:S△EDA+S△CDE+S△CEB=S四边形ABCD.
故选:D.
2.勾股定理是“人类最伟大的十个科学发现之一”.我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是( )
A.
B.
C.
D.
【分析】“赵爽弦图”是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形.
【解答】解:“赵爽弦图”是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示:
故选:B.
3.为迎接新年的到来,同学们做了许多拉花布置教室,准备召开新年晚会,小刘搬来一架高2.5米的木梯,准备把拉花挂到2.4米高的墙上,则梯脚与墙角距离应为( )
A.0.7米
B.0.8米
C.0.9米
D.1.0米
【分析】仔细分析题意得:梯子、地面、墙刚好形成一直角三角形,梯高为斜边,利用勾股定理解此直角三角形即可.
【解答】解:梯脚与墙角距离:=0.7(米).
故选:A.
4.如图,要建一个一面靠墙的西红柿大棚,棚宽a=4m,墙高b=3m,棚长d=12m,则覆盖在顶上的塑料薄膜需要的面积至少应为( )
A.36m2
B.48m2
C.60m2
D.84m2
【分析】因为b为高,所以△ABC是直角三角形,先根据勾股定理求出AB的长,再根据矩形的面积公式即可求出矩形ABDE的面积,即盖在顶上的塑料薄膜的面积.
【解答】解:∵b⊥a,
∴△ABC是直角三角形,则AB==5(m),
∴S矩形ABDE=AB?d=5×12=60(m2),
故选:C.
5.如图,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则CE的长为( )
A.3
B.3.5
C.2.5
D.2.8
【分析】根据线段垂直平分线上的点到线段两端点的距离相等的性质可得AE=CE,设CE=x,表示出ED的长度,然后在Rt△CDE中,利用勾股定理列式计算即可得解.
【解答】解:∵EO是AC的垂直平分线,
∴AE=CE,
设CE=x,则ED=AD﹣AE=4﹣x,
在Rt△CDE中,CE2=CD2+ED2,
即x2=22+(4﹣x)2,
解得x=2.5,
即CE的长为2.5.
故选:C.
6.《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A.x2﹣6=(10﹣x)2
B.x2﹣62=(10﹣x)2
C.x2+6=(10﹣x)2
D.x2+62=(10﹣x)2
【分析】根据题意画出图形,设折断处离地面的高度为x尺,再利用勾股定理列出方程即可.
【解答】解:如图,设折断处离地面的高度为x尺,则AB=10﹣x,BC=6,
在Rt△ABC中,AC2+BC2=AB2,即x2+62=(10﹣x)2.
故选:D.
7.一个圆柱形笔筒底面半径为5cm,高24cm,则笔筒内所能容下最长的笔为( )
A.20cm
B.24cm
C.26cm
D.30cm
【分析】桶内容下的木棒最长时,木棒、圆桶的直径、桶高三者正好构成一个直角三角形,根据勾股定理即可求解.
【解答】解:如图,AC为圆桶底面直径,CB是桶高,
∴AC=2×5=10(cm),CB=24cm,
∴线段AB的长度就是桶内所能容下的最长木棒的长度,
在Rt△ABC中,AC2+BC2=AB2,
AB===26(cm).
故桶内所能容下的最长木棒的长度为26cm.
故选:C.
8.如图所示的是一个十字路口,O是两条公路的交点,点A,B,C,D表示的是公路上的四辆车,若OC=6m,AC=10m,AB=12m,BD=25m,则C,D两辆车之间的距离为( )
A.9m
B.10m
C.12m
D.15m
【分析】在Rt△AOC中根据勾股定理求出OA的长,进而可得OB,在Rt△BOD中根据勾股定理可得OD的长,可得答案.
【解答】解:在Rt△AOC中,∵OA2+OC2=AC2,
∴OA=(m),
∴OB=OA+AB=20m,
在Rt△BOD中,∵BD2=OB2+OD2,
∴OD=(m),
∴CD=OD﹣OC=9m,
故选:A.
二.填空题(共6小题,4
6=24)
9.如图所示,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了 4 步路(假设2步为1米),却踩伤了花草.
【分析】本题关键是求出路长,即三角形的斜边长.求两直角边的和与斜边的差.
【解答】解:根据勾股定理可得斜边长是=5m.
则少走的距离是3+4﹣5=2m,
∵2步为1米,
∴少走了4步,
故答案为:4.
10.如图,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点之间的距离是 18 米.
【分析】运用勾股定理可将三角形的直角边求出,将两个直角边进行相加即为两个固定点之间的距离.
【解答】解:∵电线杆高为12m,铁丝长15m,
∴固定点与电线杆的距离==9m,
∵两个直角三角形全等,
∴两个固定点之间的距离=9×2=18m.
11.如图,某人从点A出发,想垂直横渡到河对岸的B点,由于水流的影响,他实际上岸的地点C偏离了想要到达的B点140米(即BC=140米),其结果是他在水中实际游了500米(即AC=500米),则该河流AB处的宽度是
480 米.
【分析】把实际问题转化为数学模型,构造直角三角形,然后利用勾股定理解决.
【解答】解:在Rt△ABC中,AB2+BC2=AC2,AC=500米,BC=140米,
所以AB===480(米).
答:该河流AB处的宽度为480米.
故答案为:480.
12.如图,一扇卷闸门用一块宽18cm,长80cm的长方形木板撑住,用这块木板最多可将这扇卷闸门撑起 82 cm高.
【分析】将长方形木板的对角线可将卷闸门撑起的最高,可用勾股定理将长方形的对角线的距离求出.
【解答】解:设长方形的长为a,宽为b,对角线的长度为c,
∵a=80cm,b=18cm,
∴c===82cm.
故最多可将这扇卷闸门撑起82cm.
13.直角三角形的一条直角边是另一条直角边的,斜边长为10,它的面积为
15 .
【分析】设一条直角边的长为x,则另一直角边为3x,根据勾股定理即可求出x.由三角形的面积公式可得出答案.
【解答】解:设一条直角边的长为x,则另一直角边为3x,
∵斜边长为10,
∴x2+(3x)2=102,
∴x=,
∴两直角边为,3,
∴直角三角形的面积为×=15.
故答案为15.
14.小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多1m,当它把绳子的下端拉开5m后,发现下端刚好接触地面,则旗杆的高为 12 m.
【分析】根据题意设旗杆的高AB为xm,则绳子AC的长为(x+1)m,再利用勾股定理即可求得AB的长,即旗杆的高.
【解答】解:设旗杆的高AB为xm,则绳子AC的长为(x+1)m.
在Rt△ABC中,AB2+BC2=AC2,
∴x2+52=(x+1)2,
解得x=12,
∴AB=12.
∴旗杆的高12m.
故答案是:12.
三.解答题(共5小题,44分)
15.(6分)用四个图1所示的直角三角形可以拼成一个如图2所示的正方形,请你用这个图形验证勾股定理.
【分析】勾股定理的证明可以通过图形的面积之间的关系来完成.
【解答】证明:∵大正方形的面积表示为(a+b)2,大正方形的面积也可表示为c2+4×ab
∴(a+b)2=c2+4×ab,a2+b2+2ab=c2+2ab,
∴a2+b2=c2,
即直角三角形两直角边的平方和等于斜边的平方.
16.(8分)甲、乙两位探险者到沙漠进行探险.某日早晨8:00甲先出发,他以6km/h的速度向东行走.1h后乙出发,他以5km/h的速度向北行进.上午10:00时,甲、乙两人相距有多远?
【分析】甲、乙行走的路线夹角为90°,根据速度和时间可以求得甲、乙行走的路程,在直角三角形中已知两直角边,根据勾股定理可以计算斜边的长.
【解答】解:甲、乙行走的路线夹角为90°,
则△ABC为直角三角形,∵早晨8:00甲先出发,
上午10:00时,甲行走的时间为:10﹣8=2小时,
∴AB=6×(10﹣8)km=12km,
∵1h后乙出发,乙行走的时间为:10﹣9=1小时,
∴AC=5×(10﹣9)km=5km,
在Rt△ABC中,BC为斜边,
则BC==13km,
答:上午10点,甲、乙两人相距13km.
17.(8分)《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图,推开双门,双门间隙C,D的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),求AB的长.
【分析】取AB的中点O,过D作DE⊥AB于E,根据勾股定理解答即可得到结论.
【解答】解:取AB的中点O,过D作DE⊥AB于E,如图所示,
由题意得OA=OB=AD=BC,DE=1尺=10寸,OE=CD=1寸,
设OA=OB=AD=BC=r寸,则AB=2r寸,AE=(r﹣1)寸.
在Rt△ADE中,AE2+DE2=AD2,
即(r﹣1)2+102=r2,
解得r=50.5.
所以2r=101,
所以AB=101寸.
18.(10分)如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,顶端距离地面的高度AC为2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面的高度A′D为2米,求小巷的宽度.
【分析】先根据勾股定理求出AB的长,同理可得出BD的长,进而可得出结论.
【解答】解:在Rt△ACB中,∵∠ACB=90°,BC=0.7米,AC=2.4米,
∴AB2=0.72+2.42=6.25.
在Rt△A′BD中,∵∠A′DB=90°,A′D=2米,BD2+A′D2=A′B′2,
∴BD2+22=6.25,
∴BD2=2.25.
∵BD>0,
∴BD=1.5米.
∴CD=BC+BD=0.7+1.5=2.2米.
答:小巷的宽度CD为2.2米.
19.(12分)在四边形ABCD中,已知AB=AD=8,∠A=60°,∠D=150°,四边形的周长为32,
(1)连接BD,试判断△ABD的形状;
(2)求BC的长.
【分析】(1)直接利用等边三角形的判定方法分析得出答案;
(2)利用勾股定理求出BC的长.
【解答】解:(1)如图,∵AB=AD=8,∠A=60°,
∴△ABD是等边三角形;
(2)∵∠BDC=150°﹣60°=90°,
∴设BC=x,
由勾股定理可知:x2=(16﹣x)2+82,
解得:x=10,
∴BC=10.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
