2013年高考数学复习专题辅导 导数与三次函数
文档属性
| 名称 | 2013年高考数学复习专题辅导 导数与三次函数 |  | |
| 格式 | zip | ||
| 文件大小 | 280.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-20 21:40:38 | ||
图片预览




文档简介
2013年高考数学复习专题辅导
导数与三次函数讲义
函数从一次,到二次,再到三次,随着“数”的增加,“形”也表现出一些新的特征.二次较一次:有了“顶点(本质上也是极值点)”、“对称轴”,“零点可有 2 个”等;三次较二次:有了“极值点”、“拐点”、“零点可有 3 个”等.即便如此,三者还是通过导数有机的联系在一起.
1.三次函数的定义.
形如 (a 0) 的函数叫做三次函数.定义域为 R ,值域为 R .
2.拐点
定义:设 f ( x) 是函数 y f (x) 的导函数 y f (x) 的导数,若 f (x) 0 有实数
解 x0 ,则称点 (x0 , f (x0 )) 为函数 y f (x) 的“拐点”.
“拐点”的定义是用二阶导数来定义的.简言之,就是导数的导数.三次函数的拐点,即一阶导函数的顶点,导函数先增后减(或先减后增)过程中的那个“转变点” 三次函数的“拐点”的重要性堪比二次函数的的“顶点”.一阶导数获得斜率,二阶导数获得拐点.一阶导数勾连三次与二次,二阶导数勾连三次与一次、二次函数.三次函数的拐点与一阶导函数的顶点、二阶导函数的零点一致.
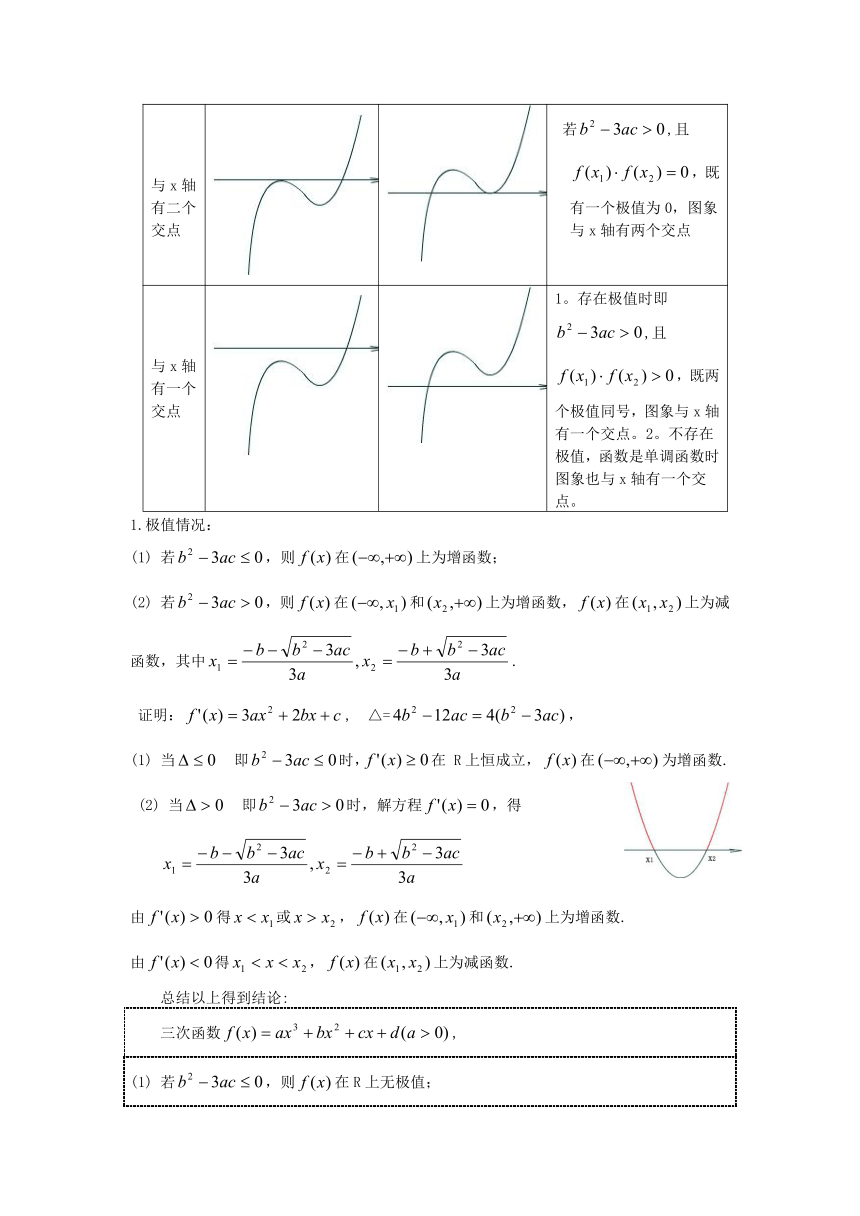
3.三次函数的图象特征、以及与x轴的交点个数(根的个数)、极值情况
三 次 函 数 图 象 说 明
a对图象的影响 可以根据极限的思想去分析当a>0时,在+∞右向上 伸展,-∞左向下伸展。当a<0时,在+∞右向下伸展,-∞左向上伸展。(可以联系二次函数a对开口的影响去联想三次函数右侧伸展情况)
与x轴有三个交点 若,且,既两个极值异号;图象与x轴有三个交点
与x轴有二个交点 若,且,既有一个极值为0,图象与x轴有两个交点
与x轴有一个交点 1。存在极值时即,且,既两个极值同号,图象与x轴有一个交点。2。不存在极值,函数是单调函数时图象也与x轴有一个交点。
1.极值情况:
(1) 若,则在上为增函数;
(2) 若,则在和上为增函数,在上为减函数,其中.
证明:, △=,
(1) 当 即时,在 R上恒成立, 在为增函数.
(2) 当 即时,解方程,得
由得或,在和上为增函数.
由得,在上为减函数.
总结以上得到结论:
三次函数,
(1) 若,则在R上无极值;
(2) 若,则在R上有两个极值;且在处取得极大值,在处取得极小值.
由此三次函数的极值要么一个也没有,要么有两个。
2.根的个数
三次函数导函数为二次函数:,
二次函数的判别式化简为:△=,
(1) 若,则恰有一个实根;
(2) 若,且,则恰有一个实根;
(3) 若,且,则有两个不相等的实根;
(4) 若,且,则有三个不相等的实根.
说明(1)(2)含有一个实根的充要条件是曲线与X轴只相交一次,即在R上为单调函数(或两极值同号),所以(或,且).
(3)有两个相异实根的充要条件是曲线与X轴有两个公共点且其中之一为切点,所以,且.
(4)有三个不相等的实根的充要条件是曲线与X轴有三个公共点,即有一个极大值,一个极小值,且两极值异号.所以且.
例1.设函数(a>0),且方程的两个根分别
为1,4
(Ⅰ)当a=3且曲线过原点时,求的解析式;
(Ⅱ)若在无极值点,求a的取值范围。
解:由 得
的两个根分别为1,4,所以 (*)(Ⅰ)当时,又由(*)式得解得
又因为曲线过原点,所以故
(Ⅱ)由于a>0,所以“在(-∞,+∞)内无极值点”等价于“在(-∞,+∞)内恒成立”。由(*)式得。
又解 得
即的取值范围
例2.已知函数f(x)=,其中a>0.
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若在区间上,f(x)>0恒成立,求a的取值范围.
【解析】(Ⅰ)解:当a=1时,f(x)=,f(2)=3;f’(x)=, f’(2)=6.所以曲线y=f(x)在点(2,f(2))处的切线方程为y-3=6(x-2),即y=6x-9.
(Ⅱ)解:f’(x)=.令f’(x)=0,解得x=0或x=.以下分两种情况讨论:
若,当x变化时,f’(x),f(x)的变化情况如下表:
X 0
f’(x) + 0 -
f(x) 极大值
当等价于,解得-5因此.
若a>2,则.当x变化时,f’(x),f(x)的变化情况如下表:
X 0
f’(x) + 0 - 0 +
f(x) 极大值 极小值
当时,f(x)>0等价于即,解不等式组得或.因此2例3.已知函数在(-∞,0)上是减函数,在(0,1)上是增函数,函数在R上有三个零点,且1是其中一个零点。 (Ⅰ)求的值;(Ⅱ)求的取值范围; (Ⅲ)设,且的解集为(-∞,1),求实数的取值范围。
解: (Ⅰ)∵f(x)=-x3+ax2+bx+c,∴. 1分
∵f(x)在在(-∞,0)上是减函数,在(0,1)上是增函数,
∴当x=0时,f(x)取到极小值,即.∴b=0. 3分
(Ⅱ)由(1)知,f(x)=-x3+ax2+c, ∵1是函数f(x)的一个零点,即f(1)=0,∴c=1-a.
∵的两个根分别为,.∵f(x)在(0,1)上是增函数,且函数f(x)在上有三个零点,∴,即.
∴.故f(2)的取值范围为.
(Ⅲ)由(Ⅱ)知,且.
∵1是函数的一个零点
又的解集为,
例4.已知函数,在点处的切线方程为.
(1)求函数的解析式;
(2)若对于区间上任意两个自变量的值,都有,求实数的最小值;
(3)若过点,可作曲线的三条切线,求实数的取值范围.
【解析】(1) 根据题意,得 即 解得
(2)令,解得,
时, 则对于区间[-2,2]上任意两个自变量,都有 所以的最小值为4。
(Ⅲ)设切点为, 切线的斜率为
则 即, 因为过点,可作曲线的三条切线所以方程有三个不同的实数解
即函数有三个不同的零点, 则
令
即,∴
【金题热身】
一、选择题:
1.若函数f(x)=x3-3x+a有3 个不同的零点,则实数a的取值范围是( )
A.(-2,2) B.[-2,2] C.(-∞,-1) D.(1,+∞)
【解析】 f′(x)=3x2-3,令f′(x)=0,∴x=±1.三次函数f(x)=0有3个根
f(x)极大值>0且f(x)极小值<0∴x=-1为极大值点,x=1为极小值点.
∴,∴-22.函数f(x)=x3+3x2+4x-a的极值点的个数是( )
A.2 B.1 C.0 D.由a确定
解析:f′(x)=3x2+6x+4=3(x+1)2+1>0,则f(x)在R上是增函数,故不存在极值点.答案:C
3.若函数f(x)=x3-ax2+1在(0,2)内单调递减,则实数a的取值范围为( )
A.a≥3 B.a=3 C.a≤3 D.0解析 ∵f(x)=x3-ax2+1在(0,2)单减∴f′(x)=3x2-2ax≤0在(0,2)恒成立,即3x2≤2ax在(0,2)上恒成立.∴a≥x在(0,2)上恒成立,∴a≥3. 答案 A
4若函数f(x)=x3-12x在区间(k-1,k+1)上不是单调函数,则实数k的取值范围是( )
A.k≤-3或-1≤k≤1或k≥3 B.-3C.-2[解析] 因为y′=3x2-12,由y′>0得函数的增区间是(-∞,-2)和(2,+∞),由y′<0,得函数的减区间是(-2,2),由于函数在(k-1,k+1)上不是单调函数,所以有k-1<-25.已知函数f(x)=x3-x2-x,则f(-a2)与f(-1)的大小关系为( )
A.f(-a2)≤f(-1) B.f(-a2)C.f(-a2)≥f(-1) D.f(-a2)与f(-1)的大小关系不确定
解析:由题意可得f′(x)=x2-2x-.由f′(x)=(3x-7)(x+1)=0,得x=-1或x=.当x<-1时,f(x)为增函数;当-16.已知函数f(x)=x3+mx2+(m+6)x+1既存在极大值又存在极小值,则实数m的取值范围是( )
A.(-1,2) B.(-∞,-3)∪(6,+∞)
C.(-3,6) D.(-∞,-1)∪(2,+∞)
解析:函数f(x)=x3+mx2+(m+6)x+1既存在极大值又存在极小值,方程f′(x)=0有两个不同的实数根,由Δ>0得m的取值范围.答案:B
7.已知函数f(x)=3x3-ax2+x-5在区间[1,2]上单调递增,则a的取值范围是( )
A.(-∞,5) B.(-∞,5]
C.(-∞,) D.(-∞,3]
解析:由题意可得f′(x)=9x2-2ax+1≥0在x∈[1,2]时恒成立.故只需满足a≤(9x+)min,x∈[1,2]即可.又由函数h(x)=x+(a>0)的单调性可知函数g(x)=9x+在[1,2]上为增函数,故a≤5. 答案:B
8.下列图象中有一个是函数f(x)=x3+ax2+(a2-1)x+1(a∈R,a≠0)的导函数f′(x)的图象,则f(-1)=( )
图1
A. B.- C. D.-
解析:f′(x)=x2+2ax+(a2-1),∵a≠0,∴其图象为最右侧的一个.由f′(0)=a2-1=0,得a=±1.由f′(x)的图象知,a<0,故a=-1,f(-1)=--1+1=-.答案:B
9. 已知某生产厂家的年利润y(单元:万元)与年产量x(单位:万件)的函数关系式为y=-x3+81x-234,则使该生产厂家获取最大年利润的年产量为 ( )
A.13万件 B.11万件
C.9万件 D.7万件
解析:y′=-x2+81,所以当x>9时,y′<0;当x∈(0,9)时,y′>0,所以函数y=-x3+81x-234在(9,+∞)上单调递减,在(0,9)上单调递增,所以x=9是函数的极大值点,又因为函数在(0,+∞)上只有一个极大值点,所以函数在x=9处取得最大值.答案:C
二、填空题:
10.函数f(x)=kx3+3(k-1)x2-k2+1(k>0)的单调减区间是(0,4),则k的值是________.
解析:f′(x)=3kx2+6(k-1)x∵函数的单调减区间是(0,4),∴f′(4)=0,∴k=.答案:
11.下图是函数y=f(x)的导函数的图象,给出下面四个判断.
①f(x)在区间[-2,-1]上是增函数; ②x=-1是f(x)的极小值点;
③f(x)在区间[-1,2]上是增函数,在区间[2,4]上是减函数;
④x=3是f(x)的极小值点.其中,所有正确判断的序号是________.
解析:由函数y=f(x)的导函数的图象可知:(1)f(x)在区间[-2,-1]上是减函数,在[-1,2]上为增函数,在[2,4]上为减函数;(2)f(x)在x=-1处取得极小值,在x=2处取得极大值.
故②③正确.答案:②③
12.已知函数f(x)=x3-bx2+c(b,c为常数).当x=2时,函数f(x)取得极值,若函数f(x)只有三个零点,则实数c的取值范围为________
解析 ∵f′(x)=x2-2bx,∵x=2时,f(x)取得极值,∴22-2b×2=0,解得b=1.∴当x∈(0,2)时,f(x)单调递减,当x∈(-∞,0) 或x∈(2,+∞)时,f(x)单调递增.若f(x)=0有3个实根,则,解得013.已知函数f(x)=x3-px2-qx的图象与x轴相切于(1,0),则极小值为________.
解析 f′(x)=3x2-2px-q,由题知f′(1)=3-2p-q=0.又f(1)=1-p-q=0,联立方程组,得p=2,q=-1.∴f(x)=x3-2x2+x,f′(x)=3x2-4x+1.由f′(x)=3x2-4x+1=0,解得x=1或x=,经检验知x=1是函数的极小值点,∴f(x)极小值=f(1)=0. 答案 0
三、解答题
14.设函数.
(1)若的两个极值点为,且,求实数的值;
(2)是否存在实数,使得是上的单调函数?若存在,求出的值;若不存在,说明理由.
[解析](1)由已知有,从而,所以;(2)由,所以不存在实数,使得是上的单调函数.
15.设的导数为,若函数的图像关于直线对称,且.(Ⅰ)求实数的值 (Ⅱ)求函数的极值
解:(I)因从而即关于直线对称,
又由于
(II)由(I)知
令
当上为增函数;
当上为减函数;
当上为增函数;
从而函数处取得极大值处取得极小值
16、已知函数=x3-ax2+b(a,b为实数,且a>1)在区间[-1,1]上的最大值为1,最小值为-2.(1)求的解析式;(2)若函数=-mx在区间[-2,2]上为减函数,求实数m的取值范围.
解:(1) =3x2-3ax,令=0,得x1=0,x2=a,∵a>1,∴在[-1,0]上为增函数,在[0,1]上为减函数.∴f(0)=b=1,∵f(-1)=-a,f(1)=2-a,∴f(-1)∴f(-1)=-a=-2,a=.∴f(x)=x3-2x2+1.
(2) =x3-2x2-mx+1,g′(x)=3x2-4x-m.由在[-2,2]上为减函数,知g′(x)≤0在x∈[-2,2]上恒成立.∴,即∴m≥20.∴实数m的取值范围是m≥20.
17.已知函数其中.
(Ⅰ)当时,求曲线在点处的切线方程;
(Ⅱ)当时,求的单调区间;
【解析】(Ⅰ)当时, ,
所以曲线在点处的切线方程为.
(Ⅱ) 令,解得或,因为,以下分两种情况讨论:
(1)若,则.当变化时, ,的变化情况如下表:
+ - +
所以的单调递增区间是,;的单调递减区间是.
+ - +
(2)若,则.当变化时, ,的变化情况如下表:
所以的单调递增区间是,;的单调递减区间是.
导数与三次函数讲义
函数从一次,到二次,再到三次,随着“数”的增加,“形”也表现出一些新的特征.二次较一次:有了“顶点(本质上也是极值点)”、“对称轴”,“零点可有 2 个”等;三次较二次:有了“极值点”、“拐点”、“零点可有 3 个”等.即便如此,三者还是通过导数有机的联系在一起.
1.三次函数的定义.
形如 (a 0) 的函数叫做三次函数.定义域为 R ,值域为 R .
2.拐点
定义:设 f ( x) 是函数 y f (x) 的导函数 y f (x) 的导数,若 f (x) 0 有实数
解 x0 ,则称点 (x0 , f (x0 )) 为函数 y f (x) 的“拐点”.
“拐点”的定义是用二阶导数来定义的.简言之,就是导数的导数.三次函数的拐点,即一阶导函数的顶点,导函数先增后减(或先减后增)过程中的那个“转变点” 三次函数的“拐点”的重要性堪比二次函数的的“顶点”.一阶导数获得斜率,二阶导数获得拐点.一阶导数勾连三次与二次,二阶导数勾连三次与一次、二次函数.三次函数的拐点与一阶导函数的顶点、二阶导函数的零点一致.
3.三次函数的图象特征、以及与x轴的交点个数(根的个数)、极值情况
三 次 函 数 图 象 说 明
a对图象的影响 可以根据极限的思想去分析当a>0时,在+∞右向上 伸展,-∞左向下伸展。当a<0时,在+∞右向下伸展,-∞左向上伸展。(可以联系二次函数a对开口的影响去联想三次函数右侧伸展情况)
与x轴有三个交点 若,且,既两个极值异号;图象与x轴有三个交点
与x轴有二个交点 若,且,既有一个极值为0,图象与x轴有两个交点
与x轴有一个交点 1。存在极值时即,且,既两个极值同号,图象与x轴有一个交点。2。不存在极值,函数是单调函数时图象也与x轴有一个交点。
1.极值情况:
(1) 若,则在上为增函数;
(2) 若,则在和上为增函数,在上为减函数,其中.
证明:, △=,
(1) 当 即时,在 R上恒成立, 在为增函数.
(2) 当 即时,解方程,得
由得或,在和上为增函数.
由得,在上为减函数.
总结以上得到结论:
三次函数,
(1) 若,则在R上无极值;
(2) 若,则在R上有两个极值;且在处取得极大值,在处取得极小值.
由此三次函数的极值要么一个也没有,要么有两个。
2.根的个数
三次函数导函数为二次函数:,
二次函数的判别式化简为:△=,
(1) 若,则恰有一个实根;
(2) 若,且,则恰有一个实根;
(3) 若,且,则有两个不相等的实根;
(4) 若,且,则有三个不相等的实根.
说明(1)(2)含有一个实根的充要条件是曲线与X轴只相交一次,即在R上为单调函数(或两极值同号),所以(或,且).
(3)有两个相异实根的充要条件是曲线与X轴有两个公共点且其中之一为切点,所以,且.
(4)有三个不相等的实根的充要条件是曲线与X轴有三个公共点,即有一个极大值,一个极小值,且两极值异号.所以且.
例1.设函数(a>0),且方程的两个根分别
为1,4
(Ⅰ)当a=3且曲线过原点时,求的解析式;
(Ⅱ)若在无极值点,求a的取值范围。
解:由 得
的两个根分别为1,4,所以 (*)(Ⅰ)当时,又由(*)式得解得
又因为曲线过原点,所以故
(Ⅱ)由于a>0,所以“在(-∞,+∞)内无极值点”等价于“在(-∞,+∞)内恒成立”。由(*)式得。
又解 得
即的取值范围
例2.已知函数f(x)=,其中a>0.
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若在区间上,f(x)>0恒成立,求a的取值范围.
【解析】(Ⅰ)解:当a=1时,f(x)=,f(2)=3;f’(x)=, f’(2)=6.所以曲线y=f(x)在点(2,f(2))处的切线方程为y-3=6(x-2),即y=6x-9.
(Ⅱ)解:f’(x)=.令f’(x)=0,解得x=0或x=.以下分两种情况讨论:
若,当x变化时,f’(x),f(x)的变化情况如下表:
X 0
f’(x) + 0 -
f(x) 极大值
当等价于,解得-5
若a>2,则.当x变化时,f’(x),f(x)的变化情况如下表:
X 0
f’(x) + 0 - 0 +
f(x) 极大值 极小值
当时,f(x)>0等价于即,解不等式组得或.因此2
解: (Ⅰ)∵f(x)=-x3+ax2+bx+c,∴. 1分
∵f(x)在在(-∞,0)上是减函数,在(0,1)上是增函数,
∴当x=0时,f(x)取到极小值,即.∴b=0. 3分
(Ⅱ)由(1)知,f(x)=-x3+ax2+c, ∵1是函数f(x)的一个零点,即f(1)=0,∴c=1-a.
∵的两个根分别为,.∵f(x)在(0,1)上是增函数,且函数f(x)在上有三个零点,∴,即.
∴.故f(2)的取值范围为.
(Ⅲ)由(Ⅱ)知,且.
∵1是函数的一个零点
又的解集为,
例4.已知函数,在点处的切线方程为.
(1)求函数的解析式;
(2)若对于区间上任意两个自变量的值,都有,求实数的最小值;
(3)若过点,可作曲线的三条切线,求实数的取值范围.
【解析】(1) 根据题意,得 即 解得
(2)令,解得,
时, 则对于区间[-2,2]上任意两个自变量,都有 所以的最小值为4。
(Ⅲ)设切点为, 切线的斜率为
则 即, 因为过点,可作曲线的三条切线所以方程有三个不同的实数解
即函数有三个不同的零点, 则
令
即,∴
【金题热身】
一、选择题:
1.若函数f(x)=x3-3x+a有3 个不同的零点,则实数a的取值范围是( )
A.(-2,2) B.[-2,2] C.(-∞,-1) D.(1,+∞)
【解析】 f′(x)=3x2-3,令f′(x)=0,∴x=±1.三次函数f(x)=0有3个根
f(x)极大值>0且f(x)极小值<0∴x=-1为极大值点,x=1为极小值点.
∴,∴-2
A.2 B.1 C.0 D.由a确定
解析:f′(x)=3x2+6x+4=3(x+1)2+1>0,则f(x)在R上是增函数,故不存在极值点.答案:C
3.若函数f(x)=x3-ax2+1在(0,2)内单调递减,则实数a的取值范围为( )
A.a≥3 B.a=3 C.a≤3 D.0
4若函数f(x)=x3-12x在区间(k-1,k+1)上不是单调函数,则实数k的取值范围是( )
A.k≤-3或-1≤k≤1或k≥3 B.-3
A.f(-a2)≤f(-1) B.f(-a2)
解析:由题意可得f′(x)=x2-2x-.由f′(x)=(3x-7)(x+1)=0,得x=-1或x=.当x<-1时,f(x)为增函数;当-1
A.(-1,2) B.(-∞,-3)∪(6,+∞)
C.(-3,6) D.(-∞,-1)∪(2,+∞)
解析:函数f(x)=x3+mx2+(m+6)x+1既存在极大值又存在极小值,方程f′(x)=0有两个不同的实数根,由Δ>0得m的取值范围.答案:B
7.已知函数f(x)=3x3-ax2+x-5在区间[1,2]上单调递增,则a的取值范围是( )
A.(-∞,5) B.(-∞,5]
C.(-∞,) D.(-∞,3]
解析:由题意可得f′(x)=9x2-2ax+1≥0在x∈[1,2]时恒成立.故只需满足a≤(9x+)min,x∈[1,2]即可.又由函数h(x)=x+(a>0)的单调性可知函数g(x)=9x+在[1,2]上为增函数,故a≤5. 答案:B
8.下列图象中有一个是函数f(x)=x3+ax2+(a2-1)x+1(a∈R,a≠0)的导函数f′(x)的图象,则f(-1)=( )
图1
A. B.- C. D.-
解析:f′(x)=x2+2ax+(a2-1),∵a≠0,∴其图象为最右侧的一个.由f′(0)=a2-1=0,得a=±1.由f′(x)的图象知,a<0,故a=-1,f(-1)=--1+1=-.答案:B
9. 已知某生产厂家的年利润y(单元:万元)与年产量x(单位:万件)的函数关系式为y=-x3+81x-234,则使该生产厂家获取最大年利润的年产量为 ( )
A.13万件 B.11万件
C.9万件 D.7万件
解析:y′=-x2+81,所以当x>9时,y′<0;当x∈(0,9)时,y′>0,所以函数y=-x3+81x-234在(9,+∞)上单调递减,在(0,9)上单调递增,所以x=9是函数的极大值点,又因为函数在(0,+∞)上只有一个极大值点,所以函数在x=9处取得最大值.答案:C
二、填空题:
10.函数f(x)=kx3+3(k-1)x2-k2+1(k>0)的单调减区间是(0,4),则k的值是________.
解析:f′(x)=3kx2+6(k-1)x∵函数的单调减区间是(0,4),∴f′(4)=0,∴k=.答案:
11.下图是函数y=f(x)的导函数的图象,给出下面四个判断.
①f(x)在区间[-2,-1]上是增函数; ②x=-1是f(x)的极小值点;
③f(x)在区间[-1,2]上是增函数,在区间[2,4]上是减函数;
④x=3是f(x)的极小值点.其中,所有正确判断的序号是________.
解析:由函数y=f(x)的导函数的图象可知:(1)f(x)在区间[-2,-1]上是减函数,在[-1,2]上为增函数,在[2,4]上为减函数;(2)f(x)在x=-1处取得极小值,在x=2处取得极大值.
故②③正确.答案:②③
12.已知函数f(x)=x3-bx2+c(b,c为常数).当x=2时,函数f(x)取得极值,若函数f(x)只有三个零点,则实数c的取值范围为________
解析 ∵f′(x)=x2-2bx,∵x=2时,f(x)取得极值,∴22-2b×2=0,解得b=1.∴当x∈(0,2)时,f(x)单调递减,当x∈(-∞,0) 或x∈(2,+∞)时,f(x)单调递增.若f(x)=0有3个实根,则,解得0
解析 f′(x)=3x2-2px-q,由题知f′(1)=3-2p-q=0.又f(1)=1-p-q=0,联立方程组,得p=2,q=-1.∴f(x)=x3-2x2+x,f′(x)=3x2-4x+1.由f′(x)=3x2-4x+1=0,解得x=1或x=,经检验知x=1是函数的极小值点,∴f(x)极小值=f(1)=0. 答案 0
三、解答题
14.设函数.
(1)若的两个极值点为,且,求实数的值;
(2)是否存在实数,使得是上的单调函数?若存在,求出的值;若不存在,说明理由.
[解析](1)由已知有,从而,所以;(2)由,所以不存在实数,使得是上的单调函数.
15.设的导数为,若函数的图像关于直线对称,且.(Ⅰ)求实数的值 (Ⅱ)求函数的极值
解:(I)因从而即关于直线对称,
又由于
(II)由(I)知
令
当上为增函数;
当上为减函数;
当上为增函数;
从而函数处取得极大值处取得极小值
16、已知函数=x3-ax2+b(a,b为实数,且a>1)在区间[-1,1]上的最大值为1,最小值为-2.(1)求的解析式;(2)若函数=-mx在区间[-2,2]上为减函数,求实数m的取值范围.
解:(1) =3x2-3ax,令=0,得x1=0,x2=a,∵a>1,∴在[-1,0]上为增函数,在[0,1]上为减函数.∴f(0)=b=1,∵f(-1)=-a,f(1)=2-a,∴f(-1)
(2) =x3-2x2-mx+1,g′(x)=3x2-4x-m.由在[-2,2]上为减函数,知g′(x)≤0在x∈[-2,2]上恒成立.∴,即∴m≥20.∴实数m的取值范围是m≥20.
17.已知函数其中.
(Ⅰ)当时,求曲线在点处的切线方程;
(Ⅱ)当时,求的单调区间;
【解析】(Ⅰ)当时, ,
所以曲线在点处的切线方程为.
(Ⅱ) 令,解得或,因为,以下分两种情况讨论:
(1)若,则.当变化时, ,的变化情况如下表:
+ - +
所以的单调递增区间是,;的单调递减区间是.
+ - +
(2)若,则.当变化时, ,的变化情况如下表:
所以的单调递增区间是,;的单调递减区间是.
同课章节目录
