第1讲统计与统计案例课件-2022届新高考数学二轮专题复习(49张PPT)
文档属性
| 名称 | 第1讲统计与统计案例课件-2022届新高考数学二轮专题复习(49张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-09 10:50:55 | ||
图片预览










文档简介
(共49张PPT)
第1讲 统计与统计案例
1.样本数据x1,x2,…,xn的数字特征
注意方差的性质
2.频率分布直方图
(1)小长方形的面积等于频率,各小长方形的面积的总和等于1;
(2)最高的小长方形底边中点的横坐标即是众数;
(3)中位数左边和右边的小长方形的面积和是相等的;
(4)平均数等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和.
误区警示1.频率分布直方图中纵轴表示的是 ,不是频率;
2.每组的频率等于该组小长方形的面积,不是该组小长方形的高.
3.变量间的相关关系
(1)如果散点图中的点从整体上看大致分布在一条直线的附近,那么我们说变量x和y具有线性相关关系.
4.独立性检验
对于取值分别是{x1,x2}和{y1,y2}的分类变量X和Y,其样本频数列联表是:
X Y 总计
y1 y2 x1 a b a+b
x2 c d c+d
总计 a+c b+d n
突破点一
用样本估计总体
考向1 用样本的数字特征估计总体的数字特征
[例1](2019全国Ⅱ,文19)某行业主管部门为了解本行业中小企业的生产情况,随机调查了100个企业,得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表.
y的分组 [-0.20,0) [0,0.20) [0.20,0.40) [0.40,0.60) [0.60,0.80)
企业数 2 24 53 14 7
(1)分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例;
(2)求这类企业产值增长率的平均数与标准差的估计值(同一组中的数据用该组区间的中点值为代表).(精确到0.01)
题后反思(1)在预测总体数据的平均值时,常用样本数据的平均值估计,从而做出合理的判断.
(2)平均数反映了数据取值的平均水平,标准差、方差描述了一组数据围绕平均数波动的大小.标准差、方差越大,数据的离散程度越大,越不稳定.
对点练1
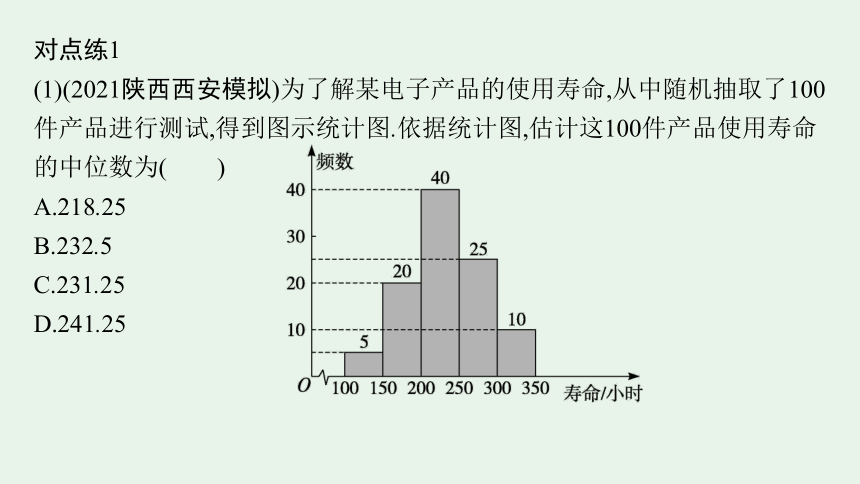
(1)(2021陕西西安模拟)为了解某电子产品的使用寿命,从中随机抽取了100件产品进行测试,得到图示统计图.依据统计图,估计这100件产品使用寿命的中位数为( )
A.218.25
B.232.5
C.231.25
D.241.25
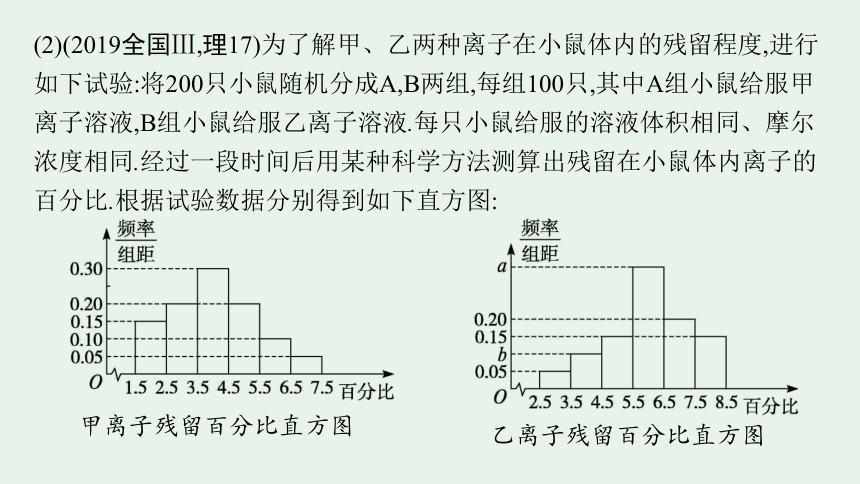
(2)(2019全国Ⅲ,理17)为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成A,B两组,每组100只,其中A组小鼠给服甲离子溶液,B组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
甲离子残留百分比直方图
乙离子残留百分比直方图
记C为事件:“乙离子残留在体内的百分比不低于5.5%”,根据直方图得到P(C)的估计值为0.70.
①求乙离子残留百分比直方图中a,b的值;
②分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
(1)C解析 设中位数为x,前2组的频数之和为25,前3组的频数之和为65,
(2)解 ①由已知得0.70=a+0.20+0.15,故a=0.35.
b=1-0.05-0.15-0.70=0.10.
②甲离子残留百分比的平均值的估计值为2×0.15+3×0.20+4×0.30+5×0.20+6×0.10+7×0.05=4.05.
乙离子残留百分比的平均值的估计值为3×0.05+4×0.10+5×0.15+6×0.35+7×0.20+8×0.15=6.00.
考向2 统计图表及其应用
[例2](1)(2021全国甲,理2)为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
(2)(2021内蒙古赤峰二模)为贯彻落实健康第一的指导思想,切实加强学校体育工作,促进学生积极参加体育锻炼,养成良好的锻炼习惯,提高体质健康水平.某市抽调三所中学进行中学生体育达标测试,现简称为A校、B校、C校.现对本次测试进行调查统计,得到测试成绩排在前200名学生层次分布的饼状图、A校前200名学生的分布条形图,则下列结论不一定正确的是( )
A.测试成绩前200名学生中B校人数超过C校人数的1.5倍
B.测试成绩前100名学生中A校人数超过一半以上
C.测试成绩在51—100名学生中A校人数多于C校人数
D.测试成绩在101—150名学生中B校人数至多有29人
答案 (1)C (2)C
解析 (1)该地农户家庭年收入低于4.5万元的农户比率估计为(0.02+0.04)×1=0.06=6%,A正确;
该地农户家庭年收入不低于10.5万元的农户比率估计为(0.04+0.02+0.02+0.02)×1=0.1=10%,B正确;
该地农户家庭年收入的平均值为0.02×3+0.04×4+0.1×5+0.14×6+0.2×7+0.2×8+0.1×9+0.1×10+0.04×11+0.02×12+0.02×13+0.02×14=7.68,C不正确;
该地农户家庭年收入介于4.5万元至8.5万元之间的比率为(0.1+0.14+0.2+0.2)×1=0.64=64%,D正确.
(2)对于A,B校人数为200×34%=68,C校人数为200×20%=40,因为68>40×1.5=60,所以A正确;
对于B,A校前100名的人数为29+25=54>50,所以B正确;
对于C,A校在51—100名的学生有25人,C校在1—200名的学生有40人,也有可能在51—100名的学生有25人,所以C不一定正确;
对于D,A校在1—100名和151—200名的学生共有29+25+17=71(人),A校在101—150名的有21人,C校在1—200名的有40人,但在101—150名的不一定有40人,而三个学校中在1—100名和151—200名内的人数至少有150人,所以B校至少有150-71-40=39(人)在1—100名和151—200名内,则B校至多有68-39=29(人)在101—150名内,所以D正确.故选C.
误区警示(1)对于给出的统计图表,一定要结合问题背景理解图表意义,不能似懂非懂.
(2)频率分布直方图中纵坐标不要误认为频率.
对点练2(1)(2021宁夏银川六盘山高级中学三模)五育并举,培养德智体美劳全面发展的社会主义建设者和接班人,某中学开展各项有益于德智体美劳全面发展的活动.如图所示是该校高三(1)、(2)班两个班级在某次活动中的德智体美劳的评价得分对照图(得分越高,说明该项教育越好).下列说法正确的是( )
A.高三(2)班五项评价得分的极差为1.5
B.高三(1)班五项评价得分的平均数比高三(2)班五项评价得分的平均数要高
C.除体育外,高三(1)班的各项评价得分均高于高三(2)班对应的得分
D.各项评价得分中,这两班的体育得分相差最大
(2)某赛季甲、乙两名篮球运动员八场比赛得分用茎叶图表示,茎叶图中甲得分的部分数据丢失,但甲得分的折线图完好,则下列结论正确的是( )
A.甲得分的极差是11
B.乙得分的中位数是18.5
C.甲运动员得分有一半在区间[20,30]上
D.甲运动员得分的平均值比乙运动员得分的平均值高
答案 (1)B (2)D
解析 (1)对于A,高三(2)班德智体美劳各项得分依次为9.5,9,9.5,9,8.5,
所以极差为9.5-8.5=1,所以A错误;
设高三(1)班劳育分为a,则9对于C,因为两班的德育分相等,所以除体育外,高三(1)班的各项评价得分不都高于高三(2)班对应的得分,所以C错误;
对于D,两班的德育分相等,智育分相差9.5-9=0.5,体育分相差9.5-9=0.5,美育分相差9.5-9=0.5,劳育分相差最大,故D错误.故选B.
突破点二
变量的相关性及回归分析
考向1 变量的线性回归分析
[例3](2021黑龙江齐齐哈尔二模)保险是指投保人根据合同约定向保险人支付保险费,保险人对于合同约定的可能发生的事故因其发生所造成的财产损失承担赔偿责任,或者被保险人死亡、伤残、疾病或者达到合同约定的年龄、期限等条件时承担给付保险金责任的商业保险行为.某研究机构对每个保险客户的回访次数x与本月的成功订单数y进行统计分析,得到x与y之间具有线性相关关系及如表数据:
回访次数x 4 5 6 8
成功订单数y 2 3 5 7
(2)试根据(1)求出的线性回归方程预测:
①若本月对每个保险客户的回访次数为10,则本月的成功订单数约为多少
②要使本月的成功订单数大于12,则本月对每个保险客户的回访最少需多少次
规律方法线性回归分析问题的类型及解题方法
1.求回归直线方程:
2.对变量值预测:
(1)若已知回归直线方程(方程中无参数),进而预测时,可以直接将数值代入求得特定要求下的预测值;
(2)若回归直线方程中有参数,则根据回归直线一定经过点 ,求出参数值,得到回归直线方程,进而完成预测.
对点练3
(2021江西赣州二模)“足球进校园”一直是热议话题.为了解某区域足球特色学校的发展状况,社会调查小组得到如下统计数据:
年份x 2016 2017 2018 2019 2020
足球特色学校y/百个 1.00 1.40 1.70 1.90 2.00
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱;
(2)求y关于x的线性回归方程,并预测该区域2022年足球特色学校的个数.
(注:当|r|≤0.25,则认为y与x的线性相关性较弱;当0.25<|r|<0.75,则认为y与x的线性相关性一般;当0.75≤|r|≤1,则认为y与x的线性相关性很强)
考向2 变量的非线性回归分析
[例4](2021辽宁丹东二模)中药藿香产业化种植已经成为某山区农民的重要产业之一,藿香在环境温度为15~28 ℃时生长旺盛,环境温度高于28 ℃或低于15 ℃时生长缓慢或停止.藿香的株高y(单位:cm)与生长期内环境温度15+x(单位:℃)中的x有关,现收集了13组藿香生长期内环境温度xi和株高yi(i=1,2,…,13)的观测数据,得到如图所示的(xi,yi)散点图.
疑难突破非线性回归方程的求法:
(1)根据原始数据作出散点图;
(2)根据散点图,选择恰当的拟合函数;
(3)做恰当变换,将其转化成线性函数,求线性回归方程;
(4)在(3)的基础上通过相应变换,即可得非线性回归方程.
特别提醒可以建立多个函数模型时,要对每个模型进行分析比较,选择最优模型.
对点练4
(2020全国Ⅰ,理5)某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:℃)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(xi,yi)(i=1,2,…,20)得到下面的散点图:
由此散点图,在10 ℃至40 ℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是( )
A.y=a+bx B.y=a+bx2
C.y=a+bex D.y=a+bln x
答案 D
解析 结合题中散点图,由图象的大致走向判断,此函数应该是对数函数模型,故应该选用的函数模型为y=a+bln x.
突破点三
独立性检验
[例5](2021全国甲,理17)甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如下表:
产品质量 一级品 二级品 合计
甲机床 150 50 200
乙机床 120 80 200
合计 270 130 400
(1)甲机床、乙机床生产的产品中一级品的频率分别是多少
(2)能否有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异
P(K2≥k0) 0.050 0.010 0.001
k0 3.841 6.635 10.828
规律方法有关独立性检验的问题解题步骤:(1)作出2×2列联表;(2)计算随机变量K2的值;(3)查临界值,检验作答.
对点练5
(2020山东,19)为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了100天空气中的PM2.5和SO2浓度(单位:μg/m3),得下表:
PM2.5 SO2 [0,50] (50,150] (150,475]
[0,35] 32 18 4
(35,75] 6 8 12
(75,115] 3 7 10
(1)估计事件“该市一天空气中PM2.5浓度不超过75,且SO2浓度不超过150”的概率;
(2)根据所给数据,完成下面的2×2列联表:
(3)根据(2)中的列联表,判断是否有99%的把握认为该市一天空气中PM2.5浓度与SO2浓度有关
PM2.5 SO2 [0,150] (150,475]
[0,75]
(75,115]
P(K2≥k0) 0.050 0.010 0.001
k0 3.841 6.635 10.828
解 (1)根据抽查数据,该市100天空气中PM2.5浓度不超过75,且SO2浓度不超过150的天数为32+18+6+8=64,因此,该市一天空气中PM2.5浓度不超过75,且SO2浓度不超过150的概率的估计值为 =0.64.
(2)根据抽查数据,可得2×2列联表:
PM2.5 SO2 [0,150] (150,475]
[0,75] 64 16
(75,115] 10 10
(3)根据(2)的列联表得K2的观测值
由于7.484>6.635,故有99%的把握认为该市一天空气中PM2.5浓度与SO2浓度有关.
第1讲 统计与统计案例
1.样本数据x1,x2,…,xn的数字特征
注意方差的性质
2.频率分布直方图
(1)小长方形的面积等于频率,各小长方形的面积的总和等于1;
(2)最高的小长方形底边中点的横坐标即是众数;
(3)中位数左边和右边的小长方形的面积和是相等的;
(4)平均数等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和.
误区警示1.频率分布直方图中纵轴表示的是 ,不是频率;
2.每组的频率等于该组小长方形的面积,不是该组小长方形的高.
3.变量间的相关关系
(1)如果散点图中的点从整体上看大致分布在一条直线的附近,那么我们说变量x和y具有线性相关关系.
4.独立性检验
对于取值分别是{x1,x2}和{y1,y2}的分类变量X和Y,其样本频数列联表是:
X Y 总计
y1 y2 x1 a b a+b
x2 c d c+d
总计 a+c b+d n
突破点一
用样本估计总体
考向1 用样本的数字特征估计总体的数字特征
[例1](2019全国Ⅱ,文19)某行业主管部门为了解本行业中小企业的生产情况,随机调查了100个企业,得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表.
y的分组 [-0.20,0) [0,0.20) [0.20,0.40) [0.40,0.60) [0.60,0.80)
企业数 2 24 53 14 7
(1)分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例;
(2)求这类企业产值增长率的平均数与标准差的估计值(同一组中的数据用该组区间的中点值为代表).(精确到0.01)
题后反思(1)在预测总体数据的平均值时,常用样本数据的平均值估计,从而做出合理的判断.
(2)平均数反映了数据取值的平均水平,标准差、方差描述了一组数据围绕平均数波动的大小.标准差、方差越大,数据的离散程度越大,越不稳定.
对点练1
(1)(2021陕西西安模拟)为了解某电子产品的使用寿命,从中随机抽取了100件产品进行测试,得到图示统计图.依据统计图,估计这100件产品使用寿命的中位数为( )
A.218.25
B.232.5
C.231.25
D.241.25
(2)(2019全国Ⅲ,理17)为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成A,B两组,每组100只,其中A组小鼠给服甲离子溶液,B组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
甲离子残留百分比直方图
乙离子残留百分比直方图
记C为事件:“乙离子残留在体内的百分比不低于5.5%”,根据直方图得到P(C)的估计值为0.70.
①求乙离子残留百分比直方图中a,b的值;
②分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
(1)C解析 设中位数为x,前2组的频数之和为25,前3组的频数之和为65,
(2)解 ①由已知得0.70=a+0.20+0.15,故a=0.35.
b=1-0.05-0.15-0.70=0.10.
②甲离子残留百分比的平均值的估计值为2×0.15+3×0.20+4×0.30+5×0.20+6×0.10+7×0.05=4.05.
乙离子残留百分比的平均值的估计值为3×0.05+4×0.10+5×0.15+6×0.35+7×0.20+8×0.15=6.00.
考向2 统计图表及其应用
[例2](1)(2021全国甲,理2)为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
(2)(2021内蒙古赤峰二模)为贯彻落实健康第一的指导思想,切实加强学校体育工作,促进学生积极参加体育锻炼,养成良好的锻炼习惯,提高体质健康水平.某市抽调三所中学进行中学生体育达标测试,现简称为A校、B校、C校.现对本次测试进行调查统计,得到测试成绩排在前200名学生层次分布的饼状图、A校前200名学生的分布条形图,则下列结论不一定正确的是( )
A.测试成绩前200名学生中B校人数超过C校人数的1.5倍
B.测试成绩前100名学生中A校人数超过一半以上
C.测试成绩在51—100名学生中A校人数多于C校人数
D.测试成绩在101—150名学生中B校人数至多有29人
答案 (1)C (2)C
解析 (1)该地农户家庭年收入低于4.5万元的农户比率估计为(0.02+0.04)×1=0.06=6%,A正确;
该地农户家庭年收入不低于10.5万元的农户比率估计为(0.04+0.02+0.02+0.02)×1=0.1=10%,B正确;
该地农户家庭年收入的平均值为0.02×3+0.04×4+0.1×5+0.14×6+0.2×7+0.2×8+0.1×9+0.1×10+0.04×11+0.02×12+0.02×13+0.02×14=7.68,C不正确;
该地农户家庭年收入介于4.5万元至8.5万元之间的比率为(0.1+0.14+0.2+0.2)×1=0.64=64%,D正确.
(2)对于A,B校人数为200×34%=68,C校人数为200×20%=40,因为68>40×1.5=60,所以A正确;
对于B,A校前100名的人数为29+25=54>50,所以B正确;
对于C,A校在51—100名的学生有25人,C校在1—200名的学生有40人,也有可能在51—100名的学生有25人,所以C不一定正确;
对于D,A校在1—100名和151—200名的学生共有29+25+17=71(人),A校在101—150名的有21人,C校在1—200名的有40人,但在101—150名的不一定有40人,而三个学校中在1—100名和151—200名内的人数至少有150人,所以B校至少有150-71-40=39(人)在1—100名和151—200名内,则B校至多有68-39=29(人)在101—150名内,所以D正确.故选C.
误区警示(1)对于给出的统计图表,一定要结合问题背景理解图表意义,不能似懂非懂.
(2)频率分布直方图中纵坐标不要误认为频率.
对点练2(1)(2021宁夏银川六盘山高级中学三模)五育并举,培养德智体美劳全面发展的社会主义建设者和接班人,某中学开展各项有益于德智体美劳全面发展的活动.如图所示是该校高三(1)、(2)班两个班级在某次活动中的德智体美劳的评价得分对照图(得分越高,说明该项教育越好).下列说法正确的是( )
A.高三(2)班五项评价得分的极差为1.5
B.高三(1)班五项评价得分的平均数比高三(2)班五项评价得分的平均数要高
C.除体育外,高三(1)班的各项评价得分均高于高三(2)班对应的得分
D.各项评价得分中,这两班的体育得分相差最大
(2)某赛季甲、乙两名篮球运动员八场比赛得分用茎叶图表示,茎叶图中甲得分的部分数据丢失,但甲得分的折线图完好,则下列结论正确的是( )
A.甲得分的极差是11
B.乙得分的中位数是18.5
C.甲运动员得分有一半在区间[20,30]上
D.甲运动员得分的平均值比乙运动员得分的平均值高
答案 (1)B (2)D
解析 (1)对于A,高三(2)班德智体美劳各项得分依次为9.5,9,9.5,9,8.5,
所以极差为9.5-8.5=1,所以A错误;
设高三(1)班劳育分为a,则9
对于D,两班的德育分相等,智育分相差9.5-9=0.5,体育分相差9.5-9=0.5,美育分相差9.5-9=0.5,劳育分相差最大,故D错误.故选B.
突破点二
变量的相关性及回归分析
考向1 变量的线性回归分析
[例3](2021黑龙江齐齐哈尔二模)保险是指投保人根据合同约定向保险人支付保险费,保险人对于合同约定的可能发生的事故因其发生所造成的财产损失承担赔偿责任,或者被保险人死亡、伤残、疾病或者达到合同约定的年龄、期限等条件时承担给付保险金责任的商业保险行为.某研究机构对每个保险客户的回访次数x与本月的成功订单数y进行统计分析,得到x与y之间具有线性相关关系及如表数据:
回访次数x 4 5 6 8
成功订单数y 2 3 5 7
(2)试根据(1)求出的线性回归方程预测:
①若本月对每个保险客户的回访次数为10,则本月的成功订单数约为多少
②要使本月的成功订单数大于12,则本月对每个保险客户的回访最少需多少次
规律方法线性回归分析问题的类型及解题方法
1.求回归直线方程:
2.对变量值预测:
(1)若已知回归直线方程(方程中无参数),进而预测时,可以直接将数值代入求得特定要求下的预测值;
(2)若回归直线方程中有参数,则根据回归直线一定经过点 ,求出参数值,得到回归直线方程,进而完成预测.
对点练3
(2021江西赣州二模)“足球进校园”一直是热议话题.为了解某区域足球特色学校的发展状况,社会调查小组得到如下统计数据:
年份x 2016 2017 2018 2019 2020
足球特色学校y/百个 1.00 1.40 1.70 1.90 2.00
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱;
(2)求y关于x的线性回归方程,并预测该区域2022年足球特色学校的个数.
(注:当|r|≤0.25,则认为y与x的线性相关性较弱;当0.25<|r|<0.75,则认为y与x的线性相关性一般;当0.75≤|r|≤1,则认为y与x的线性相关性很强)
考向2 变量的非线性回归分析
[例4](2021辽宁丹东二模)中药藿香产业化种植已经成为某山区农民的重要产业之一,藿香在环境温度为15~28 ℃时生长旺盛,环境温度高于28 ℃或低于15 ℃时生长缓慢或停止.藿香的株高y(单位:cm)与生长期内环境温度15+x(单位:℃)中的x有关,现收集了13组藿香生长期内环境温度xi和株高yi(i=1,2,…,13)的观测数据,得到如图所示的(xi,yi)散点图.
疑难突破非线性回归方程的求法:
(1)根据原始数据作出散点图;
(2)根据散点图,选择恰当的拟合函数;
(3)做恰当变换,将其转化成线性函数,求线性回归方程;
(4)在(3)的基础上通过相应变换,即可得非线性回归方程.
特别提醒可以建立多个函数模型时,要对每个模型进行分析比较,选择最优模型.
对点练4
(2020全国Ⅰ,理5)某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:℃)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(xi,yi)(i=1,2,…,20)得到下面的散点图:
由此散点图,在10 ℃至40 ℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是( )
A.y=a+bx B.y=a+bx2
C.y=a+bex D.y=a+bln x
答案 D
解析 结合题中散点图,由图象的大致走向判断,此函数应该是对数函数模型,故应该选用的函数模型为y=a+bln x.
突破点三
独立性检验
[例5](2021全国甲,理17)甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如下表:
产品质量 一级品 二级品 合计
甲机床 150 50 200
乙机床 120 80 200
合计 270 130 400
(1)甲机床、乙机床生产的产品中一级品的频率分别是多少
(2)能否有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异
P(K2≥k0) 0.050 0.010 0.001
k0 3.841 6.635 10.828
规律方法有关独立性检验的问题解题步骤:(1)作出2×2列联表;(2)计算随机变量K2的值;(3)查临界值,检验作答.
对点练5
(2020山东,19)为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了100天空气中的PM2.5和SO2浓度(单位:μg/m3),得下表:
PM2.5 SO2 [0,50] (50,150] (150,475]
[0,35] 32 18 4
(35,75] 6 8 12
(75,115] 3 7 10
(1)估计事件“该市一天空气中PM2.5浓度不超过75,且SO2浓度不超过150”的概率;
(2)根据所给数据,完成下面的2×2列联表:
(3)根据(2)中的列联表,判断是否有99%的把握认为该市一天空气中PM2.5浓度与SO2浓度有关
PM2.5 SO2 [0,150] (150,475]
[0,75]
(75,115]
P(K2≥k0) 0.050 0.010 0.001
k0 3.841 6.635 10.828
解 (1)根据抽查数据,该市100天空气中PM2.5浓度不超过75,且SO2浓度不超过150的天数为32+18+6+8=64,因此,该市一天空气中PM2.5浓度不超过75,且SO2浓度不超过150的概率的估计值为 =0.64.
(2)根据抽查数据,可得2×2列联表:
PM2.5 SO2 [0,150] (150,475]
[0,75] 64 16
(75,115] 10 10
(3)根据(2)的列联表得K2的观测值
由于7.484>6.635,故有99%的把握认为该市一天空气中PM2.5浓度与SO2浓度有关.
同课章节目录
