第1讲空间几何体的结构、表面积与体积课件-2022届新高考数学二轮专题复习(38张PPT)
文档属性
| 名称 | 第1讲空间几何体的结构、表面积与体积课件-2022届新高考数学二轮专题复习(38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 14:05:15 | ||
图片预览











文档简介
(共38张PPT)
第1讲 空间几何体的结构、表面积与体积
1.空间几何体的表面积与体积
(1)棱柱、棱锥、棱台的表面积与体积
①棱柱、棱锥、棱台的表面积
棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和.
②棱柱、棱锥、棱台的体积
V棱柱=Sh(S为底面面积,h为高),
(2)圆柱、圆锥、圆台的表面积与体积
①圆柱、圆锥、圆台的表面积
S圆柱=2πr(r+l)(r为底面半径,l为母线长),
S圆锥=πr(r+l)(r为底面半径,l为母线长),
S圆台=π(r'2+r2+r'l+rl)(r',r分别为上、下底面半径,l为母线长).
②圆柱、圆锥、圆台的体积
V圆柱=πr2h(r为底面半径,h为高),
(3)球的表面积与体积
①球的表面积
S球=4πR2(R为半径).
②球的体积
温馨提示求几何体体积常用的方法是:(1)公式法;(2)等积法;(3)割补法.
2.几个常用结论
(1)若长方体从一个顶点出发的三条棱长分别为a,b,c,则其体对角线(即外接球的直径)为
(2)正四面体(棱长都为a)的几个结论:
易错警示正四面体一定是正三棱锥,但正三棱锥不一定是正四面体.
突破点一
空间几何体的结构特征
答案 B
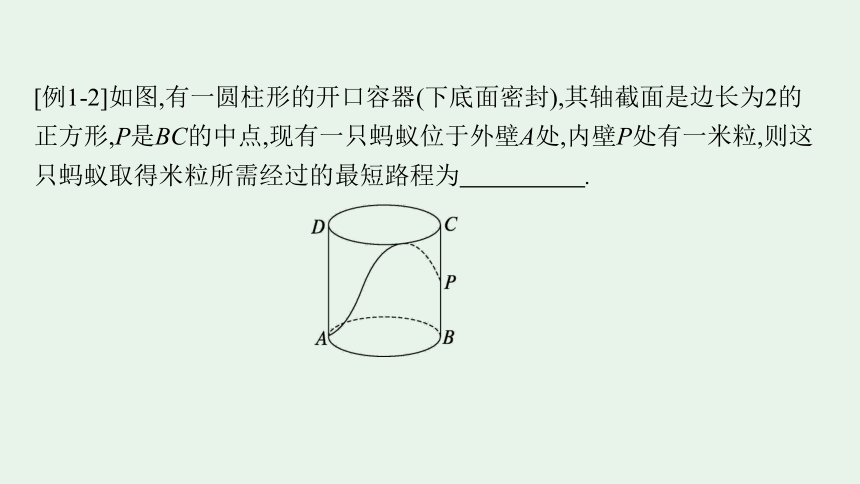
[例1-2]如图,有一圆柱形的开口容器(下底面密封),其轴截面是边长为2的正方形,P是BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一米粒,则这只蚂蚁取得米粒所需经过的最短路程为 .
对点练1
(1)(2021·山东淄博二模)已知圆台的上、下底面面积分别为4,16,则过该圆台的母线的中点,且平行于底面的平面截该圆台,所得截面的面积为( )
A.10 B.8 C.9 D.8
答案 C
(2)(2021·广东江门一模)如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点,当A1M+MC取最小值时,B1M的长为( )
答案 D
突破点二
空间几何体的表面积
[例2-1](2021·福建厦门二模)国家游泳中心(水立方)的设计灵感来源于威尔-弗兰泡沫,威尔-弗兰泡沫是对开尔文胞体的改进,开尔文胞体是一种多面体,它由正六边形和正方形围成(其中每个顶点处有1个正方形和2个正六边形),已知该多面体共有24个顶点,且棱长为1,则该多面体的表面积是( )
答案 C
[例2-2](2021·全国甲,文14)已知一个圆锥的底面半径为6,其体积为30π,则该圆锥的侧面积为 .
答案 39π
解析 设圆锥的高为h,母线长为l,
对点练2
(1)(2021·山西太原三模)现有一个橡皮泥制作的圆柱,其底面半径、高均为2,将它重新制作成一个体积与高不变的圆锥,则该圆锥的侧面积为( )
答案 B
(2)(2021·江苏镇江期中)刍甍是中国古代数学中的一种几何体.《九章算术》中记载:“刍甍者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”翻译为“刍甍的底面有长有宽为矩形,顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶”.一刍甍的直观图如图所示,其中前后两个面为全等的等腰梯形,则搭建它(无底面,不考虑厚度)需要茅草覆盖的面积至少为( )
答案 B
突破点三
空间几何体的体积
答案 A
解析 设圆锥的底面半径为r,母线长为l,高为h,因为圆锥的轴截面是等腰直
[例3-2](2021·江苏常熟中学三模)已知四棱锥P-ABCD的体积为V,四边形ABCD为平行四边形,E,F分别为棱PC,PD的中点,则四棱锥P-ABEF的体积为 (用V表示).
方法总结求几何体体积的基本方法
(1)直接法:对于规则的几何体,可利用相关公式直接计算求解.
(2)割补法:对于不规则的几何体,可将其分割成规则的几何体,进行体积计算;也可把不规则的几何体补成规则的几何体,进行体积计算.
(3)转换法:主要用于求三棱锥(四面体)的体积,将三棱锥的顶点和底面进行转换,使其底面的面积可求(或容易求),高可求(或容易求),从而代入公式求得体积.
对点练3
(1)(2021·山东烟台三模)陀螺是中国民间最早的娱乐工具之一.传统陀螺大致是木制或铁制的,玩法是用鞭子抽.如图,一个倒置的木制陀螺可看成由圆锥和圆柱组成,上面为圆锥,下面为同底圆柱,其总高度为8 cm,圆柱部分高度为6 cm,已知该陀螺由密度为0.7 g/cm3的木质材料做成,其总质量为70 g,则此陀螺圆柱底面半径的长度约为( )
A.2.2 cm B.2.4 cm
C.2.6 cm D.2.8 cm
答案(1)A (2) D
突破点四
与球有关的接切问题
[例4-1](2021·甘肃兰州月考)已知四棱锥P-ABCD的底面ABCD是矩形,AD=1,AB=2,侧棱PA⊥底面ABCD,且直线PB与CD所成角的余弦值为 ,则四棱锥P-ABCD的外接球的表面积为 .
答案 6π
方法总结解决几何体外接球问题的基本方法
(1)由球的定义确定球心.
①正方体或长方体的外接球的球心是其体对角线的中点.
②正棱柱的外接球的球心是上、下底面中心的连线的中点.
③直三棱柱的外接球的球心是上、下底面三角形外心的连线的中点.
④正棱锥的外接球的球心在其高上,具体位置可通过构造直角三角形,利用勾股定理求得.
(2)构造正方体或长方体确定球心.
①可构造正方体的情况:a.正四面体,其棱长对应正方体的面对角线长;b.三条侧棱两两垂直的正三
棱锥,其底面边长对应正方体的面对角线长,侧棱长对应正方体的棱长.
②可构造长方体的情况:a.某一个顶点处的三条棱两两垂直的四面体;b.四个面都是直角三角形的三棱锥;c.相对的棱相等的三棱锥.
(3)利用性质确定球心.
对点练4
(2021·山东泰安一模)已知三棱柱的侧棱垂直于底面,所有棱长都为1,顶点都在一个球面上,则该球的表面积为( )
答案 D
命题角度2 几何体的内切球问题
[例4-2](2021·广东深圳二模)若在母线长为5,高为4的圆锥中挖去一个小球,则剩余部分的体积的最小值为 .
名师点析求几何体内切球的半径的常用方法
(1)将空间问题转化为平面问题,通过构造直角三角形,利用平面知识求出内切球的半径.
(2)利用体积分割求出内切球的半径.
对点练5
答案 B
解析 如图,取AD的中点E,BC的中点F,连接PE,EF,PF,则由平面PAD⊥平面ABCD,可知PE⊥平面ABCD,所以PE⊥EF.由题意及对称性可知四棱锥P-ABCD内可以放置的最大球的半径即为Rt△PEF内切圆的半径.因为
第1讲 空间几何体的结构、表面积与体积
1.空间几何体的表面积与体积
(1)棱柱、棱锥、棱台的表面积与体积
①棱柱、棱锥、棱台的表面积
棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和.
②棱柱、棱锥、棱台的体积
V棱柱=Sh(S为底面面积,h为高),
(2)圆柱、圆锥、圆台的表面积与体积
①圆柱、圆锥、圆台的表面积
S圆柱=2πr(r+l)(r为底面半径,l为母线长),
S圆锥=πr(r+l)(r为底面半径,l为母线长),
S圆台=π(r'2+r2+r'l+rl)(r',r分别为上、下底面半径,l为母线长).
②圆柱、圆锥、圆台的体积
V圆柱=πr2h(r为底面半径,h为高),
(3)球的表面积与体积
①球的表面积
S球=4πR2(R为半径).
②球的体积
温馨提示求几何体体积常用的方法是:(1)公式法;(2)等积法;(3)割补法.
2.几个常用结论
(1)若长方体从一个顶点出发的三条棱长分别为a,b,c,则其体对角线(即外接球的直径)为
(2)正四面体(棱长都为a)的几个结论:
易错警示正四面体一定是正三棱锥,但正三棱锥不一定是正四面体.
突破点一
空间几何体的结构特征
答案 B
[例1-2]如图,有一圆柱形的开口容器(下底面密封),其轴截面是边长为2的正方形,P是BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一米粒,则这只蚂蚁取得米粒所需经过的最短路程为 .
对点练1
(1)(2021·山东淄博二模)已知圆台的上、下底面面积分别为4,16,则过该圆台的母线的中点,且平行于底面的平面截该圆台,所得截面的面积为( )
A.10 B.8 C.9 D.8
答案 C
(2)(2021·广东江门一模)如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点,当A1M+MC取最小值时,B1M的长为( )
答案 D
突破点二
空间几何体的表面积
[例2-1](2021·福建厦门二模)国家游泳中心(水立方)的设计灵感来源于威尔-弗兰泡沫,威尔-弗兰泡沫是对开尔文胞体的改进,开尔文胞体是一种多面体,它由正六边形和正方形围成(其中每个顶点处有1个正方形和2个正六边形),已知该多面体共有24个顶点,且棱长为1,则该多面体的表面积是( )
答案 C
[例2-2](2021·全国甲,文14)已知一个圆锥的底面半径为6,其体积为30π,则该圆锥的侧面积为 .
答案 39π
解析 设圆锥的高为h,母线长为l,
对点练2
(1)(2021·山西太原三模)现有一个橡皮泥制作的圆柱,其底面半径、高均为2,将它重新制作成一个体积与高不变的圆锥,则该圆锥的侧面积为( )
答案 B
(2)(2021·江苏镇江期中)刍甍是中国古代数学中的一种几何体.《九章算术》中记载:“刍甍者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”翻译为“刍甍的底面有长有宽为矩形,顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶”.一刍甍的直观图如图所示,其中前后两个面为全等的等腰梯形,则搭建它(无底面,不考虑厚度)需要茅草覆盖的面积至少为( )
答案 B
突破点三
空间几何体的体积
答案 A
解析 设圆锥的底面半径为r,母线长为l,高为h,因为圆锥的轴截面是等腰直
[例3-2](2021·江苏常熟中学三模)已知四棱锥P-ABCD的体积为V,四边形ABCD为平行四边形,E,F分别为棱PC,PD的中点,则四棱锥P-ABEF的体积为 (用V表示).
方法总结求几何体体积的基本方法
(1)直接法:对于规则的几何体,可利用相关公式直接计算求解.
(2)割补法:对于不规则的几何体,可将其分割成规则的几何体,进行体积计算;也可把不规则的几何体补成规则的几何体,进行体积计算.
(3)转换法:主要用于求三棱锥(四面体)的体积,将三棱锥的顶点和底面进行转换,使其底面的面积可求(或容易求),高可求(或容易求),从而代入公式求得体积.
对点练3
(1)(2021·山东烟台三模)陀螺是中国民间最早的娱乐工具之一.传统陀螺大致是木制或铁制的,玩法是用鞭子抽.如图,一个倒置的木制陀螺可看成由圆锥和圆柱组成,上面为圆锥,下面为同底圆柱,其总高度为8 cm,圆柱部分高度为6 cm,已知该陀螺由密度为0.7 g/cm3的木质材料做成,其总质量为70 g,则此陀螺圆柱底面半径的长度约为( )
A.2.2 cm B.2.4 cm
C.2.6 cm D.2.8 cm
答案(1)A (2) D
突破点四
与球有关的接切问题
[例4-1](2021·甘肃兰州月考)已知四棱锥P-ABCD的底面ABCD是矩形,AD=1,AB=2,侧棱PA⊥底面ABCD,且直线PB与CD所成角的余弦值为 ,则四棱锥P-ABCD的外接球的表面积为 .
答案 6π
方法总结解决几何体外接球问题的基本方法
(1)由球的定义确定球心.
①正方体或长方体的外接球的球心是其体对角线的中点.
②正棱柱的外接球的球心是上、下底面中心的连线的中点.
③直三棱柱的外接球的球心是上、下底面三角形外心的连线的中点.
④正棱锥的外接球的球心在其高上,具体位置可通过构造直角三角形,利用勾股定理求得.
(2)构造正方体或长方体确定球心.
①可构造正方体的情况:a.正四面体,其棱长对应正方体的面对角线长;b.三条侧棱两两垂直的正三
棱锥,其底面边长对应正方体的面对角线长,侧棱长对应正方体的棱长.
②可构造长方体的情况:a.某一个顶点处的三条棱两两垂直的四面体;b.四个面都是直角三角形的三棱锥;c.相对的棱相等的三棱锥.
(3)利用性质确定球心.
对点练4
(2021·山东泰安一模)已知三棱柱的侧棱垂直于底面,所有棱长都为1,顶点都在一个球面上,则该球的表面积为( )
答案 D
命题角度2 几何体的内切球问题
[例4-2](2021·广东深圳二模)若在母线长为5,高为4的圆锥中挖去一个小球,则剩余部分的体积的最小值为 .
名师点析求几何体内切球的半径的常用方法
(1)将空间问题转化为平面问题,通过构造直角三角形,利用平面知识求出内切球的半径.
(2)利用体积分割求出内切球的半径.
对点练5
答案 B
解析 如图,取AD的中点E,BC的中点F,连接PE,EF,PF,则由平面PAD⊥平面ABCD,可知PE⊥平面ABCD,所以PE⊥EF.由题意及对称性可知四棱锥P-ABCD内可以放置的最大球的半径即为Rt△PEF内切圆的半径.因为
同课章节目录
