第2讲空间位置关系的判断与证明课件-2022届新高考数学二轮专题复习(24张PPT)
文档属性
| 名称 | 第2讲空间位置关系的判断与证明课件-2022届新高考数学二轮专题复习(24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 677.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 14:06:13 | ||
图片预览








文档简介
(共24张PPT)
第2讲 空间位置关系的判断与证明
1.直线、平面平行的判定与性质
(1)线面平行的判定定理:a α,b α,a∥b a∥α.
(2)线面平行的性质定理:a∥α,a β,α∩β=b a∥b.
(3)面面平行的判定定理:a β,b β,a∩b=P,a∥α,b∥α β∥α.
(4)面面平行的性质定理:α∥β,α∩γ=a,β∩γ=b a∥b.
2.直线、平面垂直的判定与性质
(1)线面垂直的判定定理:m α,n α,m∩n=P,l⊥m,l⊥n l⊥α.
(2)线面垂直的性质定理:a⊥α,b⊥α a∥b.
(3)面面垂直的判定定理:a β,a⊥α β⊥α.
(4)面面垂直的性质定理:α⊥β,α∩β=l,a α,a⊥l a⊥β.
3.定义法求空间角
求空间角的大小,一般是根据相关角(异面直线所成的角、直线与平面所成的角、二面角的平面角)的定义,把空间角转化为平面角来求解.
命题角度1 有关线面位置关系的命题的真假判断
[例1-1](2021·山东青岛三模)设α,β是空间两个不同平面,a,b,c是空间三条不同直线,下列命题为真命题的是( )
A.若α∥β,b∥α,则b∥β
B.若a与b相交,a∥α,b∥β,则α与β相交
C.若α⊥β,a∥α,则a⊥β
D.若α⊥β,α∩β=a,b α,b⊥a,c⊥β,则b∥c
答案 D
解析 对于A选项,若α∥β,b∥α,则b∥β或b β,故A中命题为假命题.
对于B选项,若直线a与b相交,a∥α,b∥β,则α与β相交或平行,故B中命题为假命题.
对于C选项,若α⊥β,a∥α,则a与β的位置关系不确定,故C中命题为假命题.
对于D选项,若α⊥β,α∩β=a,b α,b⊥a,则b⊥β,又c⊥β,所以b∥c,故D中命题为真命题.故选D.
对点练1
(2021·浙江湖州二模)已知直线l,m和平面α,下列命题为真命题的是( )
A.若l∥m,m α,则l∥α
B.若l∥α,m α,则l∥m
C.若l⊥α,m α,则l⊥m
D.若l⊥m,l⊥α,则m⊥α
答案 C
解析 对于A,若l∥m,m α,则l∥α或l α,故A中命题为假命题.对于B,若l∥α,m α,则l∥m或l,m异面,故B中命题为假命题.对于C,若l⊥α,m α,则l⊥m,故C中命题为真命题.对于D,若l⊥m,l⊥α,则m∥α或m α,故D中命题为假命题.故选C.
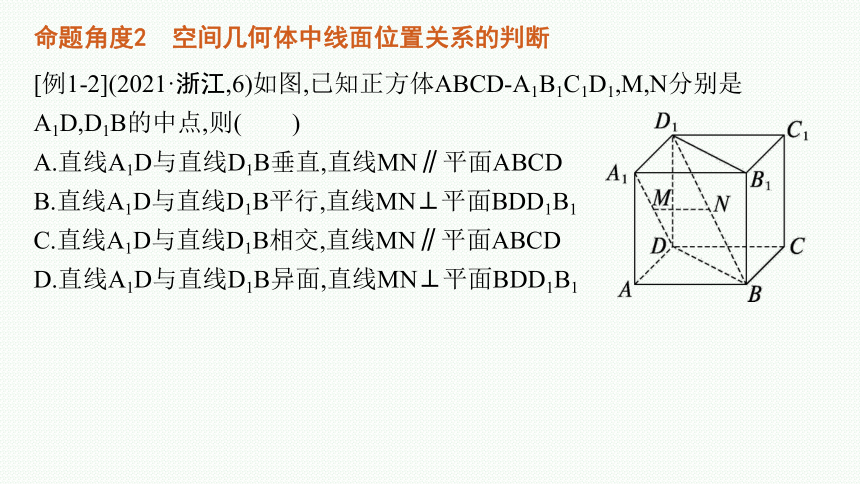
命题角度2 空间几何体中线面位置关系的判断
[例1-2](2021·浙江,6)如图,已知正方体ABCD-A1B1C1D1,M,N分别是A1D,D1B的中点,则( )
A.直线A1D与直线D1B垂直,直线MN∥平面ABCD
B.直线A1D与直线D1B平行,直线MN⊥平面BDD1B1
C.直线A1D与直线D1B相交,直线MN∥平面ABCD
D.直线A1D与直线D1B异面,直线MN⊥平面BDD1B1
答案 A
解析 如图,连接AD1,则AD1经过点M,且M为AD1的中点.
又N为BD1的中点,所以MN∥AB.
又MN 平面ABCD,AB 平面ABCD,所以MN∥平面ABCD.
易知AB不垂直于平面BDD1B1,所以MN不垂直于平面BDD1B1.
在正方体ABCD -A1B1C1D1中,AB⊥平面ADD1A1,
∵A1D 平面ADD1A1,∴AB⊥A1D.
又四边形ADD1A1为正方形,∴A1D⊥AD1.
又AD1∩AB=A,∴A1D⊥平面ABD1,
∴直线A1D与直线D1B垂直.易知直线A1D与
直线D1B异面.故选A.
对点练2
(多选题)(2021·江苏无锡期中)在正方体ABCD-A1B1C1D1中,M,N,P,Q分别是AA1,A1D1,CC1,BC的中点,则下列结论正确的是( )
A.A1C⊥MN
B.A1C∥平面MNPQ
C.A1C与PM相交
D.NC1与PM异面
答案 ACD
解析 如图,在正方体ABCD-A1B1C1D1中,A1D⊥AD1,因为CD⊥平面AA1D1D,AD1 平面AA1D1D,所以CD⊥AD1,所以AD1⊥平面A1CD,所以A1C⊥AD1.因为M,N分别是AA1,A1D1的中点,所以AD1∥MN,所以A1C⊥MN,所以A正确.在平面AA1C1C中,易知A1C与PM相交,又PM 平面MNPQ,所以A1C与平面MNPQ相交,所以B不正确,C正确.因为M,N,P∈平面MNPQ,C1 平面MNPQ,所以NC1与PM异面,所以D正确.故选ACD.
答案 D
解析 如图,连接BC1,PC1.
由正方体的性质可得AD1∥BC1,故∠PBC1为直线PB与AD1所成的角.
答案 C
对点练3
(1)(2021·河北邯郸三模)如图,圆台OO1的上底面半径为O1A1=1,下底面半径为OA=2,母线长AA1=2,过OA的中点B作OA的垂线交圆O于点C,则异面直线OO1与A1C所成角的大小为( )
A.30° B.45° C.60° D.90°
(2)(2021·山东济南二模)已知一个圆锥的侧面积是底面面积的2倍,则该圆锥的母线与其底面所成的角的大小为 .
解析 (1)如图,在直角梯形OO1A1A中,∵B为OA的中点,OA=2,∴O1A1=OB=AB=1,连接A1B,易知四边形OO1A1B为矩形,∴OO1∥A1B,∴∠BA1C为异面直线OO1与A1C所成的角.
在Rt△AA1B中,AA1=2,AB=1,
[例3]如图,在正方体ABCD-A1B1C1D1中,点P在线段AD1上运动,给出以下四个结论:
①三棱锥D-BPC1的体积为定值;②异面直线C1P与CB1所成的角为定值;③二面角P-BC1-D的大小为定值.其中正确结论有( )
A.0个 B.1个 C.2个 D.3个
答案 D
BDC1,所以点P到平面BDC1的距离等于点A到平面BDC1的距离,而点A到平面BDC1的距离为定值,所以三棱锥D-BPC1的体积为定值,故①正确.对于②,在正方体ABCD-A1B1C1D1中,易知B1C⊥平面ABC1D1,而C1P 平面ABC1D1,所以B1C⊥C1P,所以异面直线C1P与CB1所成的角为90°,为定值,故②正确.对于③,二面角P-BC1-D的大小,即为平面ABC1D1与平面BDC1所成二面角的大小,而这两个平面位置固定不变,故二面角P-BC1-D的大小为定值,故③正确.故选D.
对点练4
(多选题)(2021·重庆二模)如图,在长方体ABCD-A1B1C1D1中,P为AA1的中点,AB=4,BC=3,BB1=8,点M在面AA1B1B内运动,则下列说法正确的是( )
A.存在点M,使BM∥CP
C.存在点M(异于点P),使P,M,C,D1四点共面
D.若点M到面ABCD的距离与它到点A1的距离相等,则点M的轨迹是抛物线的一部分
答案 BCD
解析 对于A,假设存在点M,使BM∥CP,因为BM 平面ABB1A1,CP 平面ABB1A1,所以CP∥平面ABB1A1,与CP∩平面ABB1A1=P矛盾,所以A错误.对于B,如图,连接AC,因为AB=4,BC=3,AB⊥BC,所以AC=5.因为P为AA1的
正确.对于C,如图,取AB的中点N,连接PN,A1B,D1C,因为PN∥A1B,A1B∥
D1C,所以PN∥D1C,所以PN与D1C共面,所以当M∈PN,且点M异于点P时,P,M,C,D1四点共面,所以C正确.对于D,由题意可知点M到平面ABCD的距离即点M到直线AB的距离,所以点M到直线AB的距离与它到点A1的距离相等,由抛物线的定义,可知点M的轨迹是抛物线的一部分,所以D正确.故选BCD.
第2讲 空间位置关系的判断与证明
1.直线、平面平行的判定与性质
(1)线面平行的判定定理:a α,b α,a∥b a∥α.
(2)线面平行的性质定理:a∥α,a β,α∩β=b a∥b.
(3)面面平行的判定定理:a β,b β,a∩b=P,a∥α,b∥α β∥α.
(4)面面平行的性质定理:α∥β,α∩γ=a,β∩γ=b a∥b.
2.直线、平面垂直的判定与性质
(1)线面垂直的判定定理:m α,n α,m∩n=P,l⊥m,l⊥n l⊥α.
(2)线面垂直的性质定理:a⊥α,b⊥α a∥b.
(3)面面垂直的判定定理:a β,a⊥α β⊥α.
(4)面面垂直的性质定理:α⊥β,α∩β=l,a α,a⊥l a⊥β.
3.定义法求空间角
求空间角的大小,一般是根据相关角(异面直线所成的角、直线与平面所成的角、二面角的平面角)的定义,把空间角转化为平面角来求解.
命题角度1 有关线面位置关系的命题的真假判断
[例1-1](2021·山东青岛三模)设α,β是空间两个不同平面,a,b,c是空间三条不同直线,下列命题为真命题的是( )
A.若α∥β,b∥α,则b∥β
B.若a与b相交,a∥α,b∥β,则α与β相交
C.若α⊥β,a∥α,则a⊥β
D.若α⊥β,α∩β=a,b α,b⊥a,c⊥β,则b∥c
答案 D
解析 对于A选项,若α∥β,b∥α,则b∥β或b β,故A中命题为假命题.
对于B选项,若直线a与b相交,a∥α,b∥β,则α与β相交或平行,故B中命题为假命题.
对于C选项,若α⊥β,a∥α,则a与β的位置关系不确定,故C中命题为假命题.
对于D选项,若α⊥β,α∩β=a,b α,b⊥a,则b⊥β,又c⊥β,所以b∥c,故D中命题为真命题.故选D.
对点练1
(2021·浙江湖州二模)已知直线l,m和平面α,下列命题为真命题的是( )
A.若l∥m,m α,则l∥α
B.若l∥α,m α,则l∥m
C.若l⊥α,m α,则l⊥m
D.若l⊥m,l⊥α,则m⊥α
答案 C
解析 对于A,若l∥m,m α,则l∥α或l α,故A中命题为假命题.对于B,若l∥α,m α,则l∥m或l,m异面,故B中命题为假命题.对于C,若l⊥α,m α,则l⊥m,故C中命题为真命题.对于D,若l⊥m,l⊥α,则m∥α或m α,故D中命题为假命题.故选C.
命题角度2 空间几何体中线面位置关系的判断
[例1-2](2021·浙江,6)如图,已知正方体ABCD-A1B1C1D1,M,N分别是A1D,D1B的中点,则( )
A.直线A1D与直线D1B垂直,直线MN∥平面ABCD
B.直线A1D与直线D1B平行,直线MN⊥平面BDD1B1
C.直线A1D与直线D1B相交,直线MN∥平面ABCD
D.直线A1D与直线D1B异面,直线MN⊥平面BDD1B1
答案 A
解析 如图,连接AD1,则AD1经过点M,且M为AD1的中点.
又N为BD1的中点,所以MN∥AB.
又MN 平面ABCD,AB 平面ABCD,所以MN∥平面ABCD.
易知AB不垂直于平面BDD1B1,所以MN不垂直于平面BDD1B1.
在正方体ABCD -A1B1C1D1中,AB⊥平面ADD1A1,
∵A1D 平面ADD1A1,∴AB⊥A1D.
又四边形ADD1A1为正方形,∴A1D⊥AD1.
又AD1∩AB=A,∴A1D⊥平面ABD1,
∴直线A1D与直线D1B垂直.易知直线A1D与
直线D1B异面.故选A.
对点练2
(多选题)(2021·江苏无锡期中)在正方体ABCD-A1B1C1D1中,M,N,P,Q分别是AA1,A1D1,CC1,BC的中点,则下列结论正确的是( )
A.A1C⊥MN
B.A1C∥平面MNPQ
C.A1C与PM相交
D.NC1与PM异面
答案 ACD
解析 如图,在正方体ABCD-A1B1C1D1中,A1D⊥AD1,因为CD⊥平面AA1D1D,AD1 平面AA1D1D,所以CD⊥AD1,所以AD1⊥平面A1CD,所以A1C⊥AD1.因为M,N分别是AA1,A1D1的中点,所以AD1∥MN,所以A1C⊥MN,所以A正确.在平面AA1C1C中,易知A1C与PM相交,又PM 平面MNPQ,所以A1C与平面MNPQ相交,所以B不正确,C正确.因为M,N,P∈平面MNPQ,C1 平面MNPQ,所以NC1与PM异面,所以D正确.故选ACD.
答案 D
解析 如图,连接BC1,PC1.
由正方体的性质可得AD1∥BC1,故∠PBC1为直线PB与AD1所成的角.
答案 C
对点练3
(1)(2021·河北邯郸三模)如图,圆台OO1的上底面半径为O1A1=1,下底面半径为OA=2,母线长AA1=2,过OA的中点B作OA的垂线交圆O于点C,则异面直线OO1与A1C所成角的大小为( )
A.30° B.45° C.60° D.90°
(2)(2021·山东济南二模)已知一个圆锥的侧面积是底面面积的2倍,则该圆锥的母线与其底面所成的角的大小为 .
解析 (1)如图,在直角梯形OO1A1A中,∵B为OA的中点,OA=2,∴O1A1=OB=AB=1,连接A1B,易知四边形OO1A1B为矩形,∴OO1∥A1B,∴∠BA1C为异面直线OO1与A1C所成的角.
在Rt△AA1B中,AA1=2,AB=1,
[例3]如图,在正方体ABCD-A1B1C1D1中,点P在线段AD1上运动,给出以下四个结论:
①三棱锥D-BPC1的体积为定值;②异面直线C1P与CB1所成的角为定值;③二面角P-BC1-D的大小为定值.其中正确结论有( )
A.0个 B.1个 C.2个 D.3个
答案 D
BDC1,所以点P到平面BDC1的距离等于点A到平面BDC1的距离,而点A到平面BDC1的距离为定值,所以三棱锥D-BPC1的体积为定值,故①正确.对于②,在正方体ABCD-A1B1C1D1中,易知B1C⊥平面ABC1D1,而C1P 平面ABC1D1,所以B1C⊥C1P,所以异面直线C1P与CB1所成的角为90°,为定值,故②正确.对于③,二面角P-BC1-D的大小,即为平面ABC1D1与平面BDC1所成二面角的大小,而这两个平面位置固定不变,故二面角P-BC1-D的大小为定值,故③正确.故选D.
对点练4
(多选题)(2021·重庆二模)如图,在长方体ABCD-A1B1C1D1中,P为AA1的中点,AB=4,BC=3,BB1=8,点M在面AA1B1B内运动,则下列说法正确的是( )
A.存在点M,使BM∥CP
C.存在点M(异于点P),使P,M,C,D1四点共面
D.若点M到面ABCD的距离与它到点A1的距离相等,则点M的轨迹是抛物线的一部分
答案 BCD
解析 对于A,假设存在点M,使BM∥CP,因为BM 平面ABB1A1,CP 平面ABB1A1,所以CP∥平面ABB1A1,与CP∩平面ABB1A1=P矛盾,所以A错误.对于B,如图,连接AC,因为AB=4,BC=3,AB⊥BC,所以AC=5.因为P为AA1的
正确.对于C,如图,取AB的中点N,连接PN,A1B,D1C,因为PN∥A1B,A1B∥
D1C,所以PN∥D1C,所以PN与D1C共面,所以当M∈PN,且点M异于点P时,P,M,C,D1四点共面,所以C正确.对于D,由题意可知点M到平面ABCD的距离即点M到直线AB的距离,所以点M到直线AB的距离与它到点A1的距离相等,由抛物线的定义,可知点M的轨迹是抛物线的一部分,所以D正确.故选BCD.
同课章节目录
