数列解答题专项突破练课件-2022届新高考数学二轮专项复习(49张PPT)
文档属性
| 名称 | 数列解答题专项突破练课件-2022届新高考数学二轮专项复习(49张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-12 14:54:26 | ||
图片预览





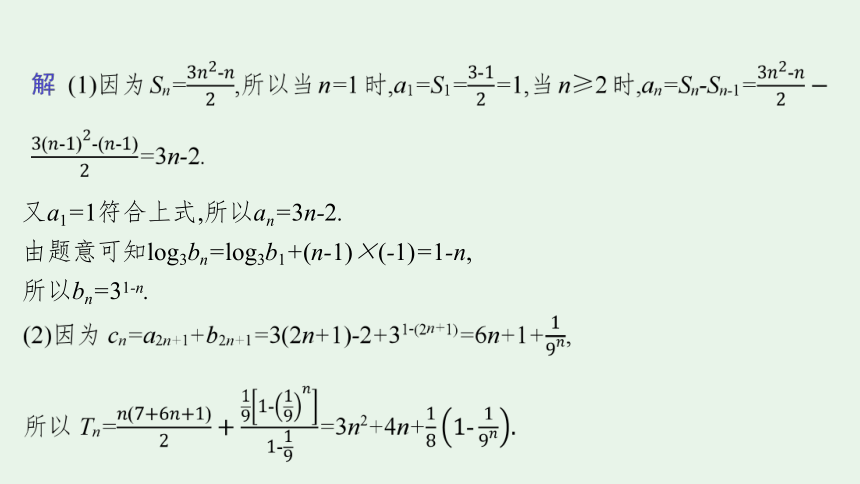


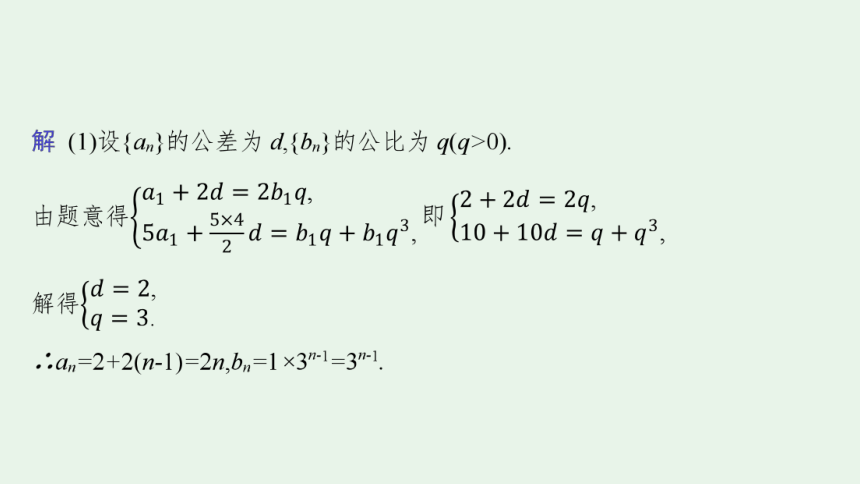



文档简介
(共49张PPT)
专项突破 数列解答题
突破
求数列的通项及前n项和
必备知识 精要梳理
1.分组转化法
具有下列特点的数列常用分组转化法求和:
(1)an=bn±cn,且{bn},{cn}为等差数列或等比数列,可采用分组转化法求和.
(2)an= 且{bn},{cn}为等差数列或等比数列,可采用分组转化法求和.
2.错位相减法
一般地,数列{an}是等差数列,{bn}是等比数列,求数列{an·bn}的前n项和时,可采用错位相减法,一般是和式两边同乘等比数列{bn}的公比,然后作差求解.
3.裂项相消法
实质是将数列的通项分解为两项之差,求和时能消去中间的一些项,最终达到求和的目的,其解题的关键是准确地裂项和消项.
(1)裂项原则:一般是前边裂几项,后边就裂几项,直到发现被消去项的规律为止.
(2)消项规律:消项后前边剩几项,后边就剩几项,前边剩第几项,后边就剩倒数第几项.
关键能力 学案突破
考向一 分组转化法求和
(1)求数列{an},{bn}的通项公式;
(2)设cn=a2n+1+b2n+1,求数列{cn}的前n项和Tn.
又a1=1符合上式,所以an=3n-2.
由题意可知log3bn=log3b1+(n-1)×(-1)=1-n,
所以bn=31-n.
解题心得分组转化法求和的技巧
(1)若能把一个较为复杂的数列的通项分成两(或多)部分,而每一部分对应的前n项和可求,则分别求和相加即可.
(2)若一个数列的前n项和不好求,而数列相邻的两项或多项的和相等且为常数,则对该数列先作并项处理,即先合并项,再求和.
精典对练·得高分
(2021·山东聊城一中一模)已知等差数列{an}的首项为2,前n项和为Sn,正项等比数列{bn}的首项为1,且满足a3=2b2,S5=b2+b4.
(1)求数列{an},{bn}的通项公式;
(2)设cn=(-1)nlog3Sn+log3bn,求数列{cn}的前26项和.
数学思想·扩思路
转化与化归思想
(2021·福建三明检测)已知等差数列{an}满足a2=4,a3+a4=17.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1=2,再从①bn+1=2bn,②2bn+1=bn,③bn+1=-bn这三个条件中任选一个作为已知,求数列{an+bn}的前n项和Tn.
点评有些数列求和问题,通过分组或并项,将不易直接求和的问题转化为容易求和的问题,这一过程体现了转化与化归的数学思想.
考向二 裂项相消法求和
精典对练·得高分
(2021·山东德州一模)已知数列{an}满足a1+2a2+3a3+…+nan=(n-1)2n+1+2.
(1)求数列{an}的通项公式;
(1)解 因为a1+2a2+3a3+…+nan=(n-1)2n+1+2,①
所以当n≥2时,a1+2a2+3a3+…+(n-1)an-1=(n-2)2n+2.②
①-②,得nan=(n-1)2n+1-(n-2)2n,即an=2n(n≥2).
当n=1时,a1=2满足上式.
所以an=2n.
一题多解·练思维
(2021·广东汕头一模)已知等比数列{an}的前n项和为Sn,给出条件:
若 ,
(1)求m的值及数列{an}的通项公式;
考向三 错位相减法求和
[例3](2021·山东日照一模)在①已知数列{an}满足:an+1-2an=0,a3=8;②等比数列{an}中,公比q=2,前5项和为62这两个条件中任选一个,并解答下列问题.
(1)求数列{an}的通项公式;
(2)设bn= ,数列{bn}的前n项和为Tn,若2Tn>m-2 022对 n∈N*恒成立,求正整数m的最大值.
精典对练·得高分
(1)解 设{an}的公比为q,则an=qn-1.
因为a1,3a2,9a3成等差数列,
易错防范·不丢分
(2021·山东青岛期末)在①4Sn=+2an,②a1=2,nan+1=2Sn这两个条件中任选一个,补充到下面横线处,并解答.
已知正项数列{an}的前n项和为Sn, .
(1)求数列{an}的通项公式;
即(an+1+an)(an+1-an-2)=0.
因为an>0,所以an+1-an=2,
所以数列{an}是首项为2,公差为2的等差数列,所以an=2n.
选②,因为nan+1=2Sn,所以当n≥2时,(n-1)an=2Sn-1,
所以nan+1-(n-1)an=2Sn-2Sn-1=2an,即nan+1=(n+1)an,
考向四 数列中的存在性问题
[例4]已知各项均为正数的等比数列{an}中,a1+a3=10,a3+a5=40.设bn=log2an.
(1)求数列{bn}的通项公式.
(1)解 设各项均为正数的等比数列{an}的公比为q(q>0),
则a1+a1q2=10,a1q2+a1q4=40,
解得a1=2,q=2,所以an=2n,bn=log22n=n.
又k为正整数,所以k的最大值为4.
故存在正整数k,且k的最大值为4.
精典对练·得高分
(2021·湖北襄阳模拟)在①{bn}为等比数列,b1=a1,3b2=a2,②{bn}为等差数列,2b1=a1,4b2=a2,③{bn}为等比数列,b1=a1+2,b2=a2+4这三个条件中任选一个,补充在下面的问题中,并解答.
又a1=2满足an=(2n-1)·2n,所以an=(2n-1)·2n.
若选①,设等比数列{bn}的公比为q(q≠0).
由已知得b1=2,b2=2q=4,则q=2,所以bn=2×2n-1=2n.
由Sk=k2≥2 020,k∈N*,可得k≥45,所以存在正整数k,使得Sk≥2 020成立,且k的最小值为45.
若选②,设等差数列{bn}的公差为d.
由已知得b1=1,b2=3,则d=b2-b1=2,
由Sk=2k+1-2≥2 020,k∈N*得k≥10,所以存在正整数k,使得Sk≥2 020成立,且k的最小值为10.
若选③,设等比数列{bn}的公比为q(q≠0).
数学思想·扩思路
函数与方程思想
(2021·江西南昌一中月考)在数列{an}中,a1=1,a1+2a2+3a3+…+nan=
an+1.
(1)求数列{an}的通项公式;
(2)若存在n∈N*,使得an≥(n+1)3nλ成立,求实数λ的最大值.
专项突破 数列解答题
突破
求数列的通项及前n项和
必备知识 精要梳理
1.分组转化法
具有下列特点的数列常用分组转化法求和:
(1)an=bn±cn,且{bn},{cn}为等差数列或等比数列,可采用分组转化法求和.
(2)an= 且{bn},{cn}为等差数列或等比数列,可采用分组转化法求和.
2.错位相减法
一般地,数列{an}是等差数列,{bn}是等比数列,求数列{an·bn}的前n项和时,可采用错位相减法,一般是和式两边同乘等比数列{bn}的公比,然后作差求解.
3.裂项相消法
实质是将数列的通项分解为两项之差,求和时能消去中间的一些项,最终达到求和的目的,其解题的关键是准确地裂项和消项.
(1)裂项原则:一般是前边裂几项,后边就裂几项,直到发现被消去项的规律为止.
(2)消项规律:消项后前边剩几项,后边就剩几项,前边剩第几项,后边就剩倒数第几项.
关键能力 学案突破
考向一 分组转化法求和
(1)求数列{an},{bn}的通项公式;
(2)设cn=a2n+1+b2n+1,求数列{cn}的前n项和Tn.
又a1=1符合上式,所以an=3n-2.
由题意可知log3bn=log3b1+(n-1)×(-1)=1-n,
所以bn=31-n.
解题心得分组转化法求和的技巧
(1)若能把一个较为复杂的数列的通项分成两(或多)部分,而每一部分对应的前n项和可求,则分别求和相加即可.
(2)若一个数列的前n项和不好求,而数列相邻的两项或多项的和相等且为常数,则对该数列先作并项处理,即先合并项,再求和.
精典对练·得高分
(2021·山东聊城一中一模)已知等差数列{an}的首项为2,前n项和为Sn,正项等比数列{bn}的首项为1,且满足a3=2b2,S5=b2+b4.
(1)求数列{an},{bn}的通项公式;
(2)设cn=(-1)nlog3Sn+log3bn,求数列{cn}的前26项和.
数学思想·扩思路
转化与化归思想
(2021·福建三明检测)已知等差数列{an}满足a2=4,a3+a4=17.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1=2,再从①bn+1=2bn,②2bn+1=bn,③bn+1=-bn这三个条件中任选一个作为已知,求数列{an+bn}的前n项和Tn.
点评有些数列求和问题,通过分组或并项,将不易直接求和的问题转化为容易求和的问题,这一过程体现了转化与化归的数学思想.
考向二 裂项相消法求和
精典对练·得高分
(2021·山东德州一模)已知数列{an}满足a1+2a2+3a3+…+nan=(n-1)2n+1+2.
(1)求数列{an}的通项公式;
(1)解 因为a1+2a2+3a3+…+nan=(n-1)2n+1+2,①
所以当n≥2时,a1+2a2+3a3+…+(n-1)an-1=(n-2)2n+2.②
①-②,得nan=(n-1)2n+1-(n-2)2n,即an=2n(n≥2).
当n=1时,a1=2满足上式.
所以an=2n.
一题多解·练思维
(2021·广东汕头一模)已知等比数列{an}的前n项和为Sn,给出条件:
若 ,
(1)求m的值及数列{an}的通项公式;
考向三 错位相减法求和
[例3](2021·山东日照一模)在①已知数列{an}满足:an+1-2an=0,a3=8;②等比数列{an}中,公比q=2,前5项和为62这两个条件中任选一个,并解答下列问题.
(1)求数列{an}的通项公式;
(2)设bn= ,数列{bn}的前n项和为Tn,若2Tn>m-2 022对 n∈N*恒成立,求正整数m的最大值.
精典对练·得高分
(1)解 设{an}的公比为q,则an=qn-1.
因为a1,3a2,9a3成等差数列,
易错防范·不丢分
(2021·山东青岛期末)在①4Sn=+2an,②a1=2,nan+1=2Sn这两个条件中任选一个,补充到下面横线处,并解答.
已知正项数列{an}的前n项和为Sn, .
(1)求数列{an}的通项公式;
即(an+1+an)(an+1-an-2)=0.
因为an>0,所以an+1-an=2,
所以数列{an}是首项为2,公差为2的等差数列,所以an=2n.
选②,因为nan+1=2Sn,所以当n≥2时,(n-1)an=2Sn-1,
所以nan+1-(n-1)an=2Sn-2Sn-1=2an,即nan+1=(n+1)an,
考向四 数列中的存在性问题
[例4]已知各项均为正数的等比数列{an}中,a1+a3=10,a3+a5=40.设bn=log2an.
(1)求数列{bn}的通项公式.
(1)解 设各项均为正数的等比数列{an}的公比为q(q>0),
则a1+a1q2=10,a1q2+a1q4=40,
解得a1=2,q=2,所以an=2n,bn=log22n=n.
又k为正整数,所以k的最大值为4.
故存在正整数k,且k的最大值为4.
精典对练·得高分
(2021·湖北襄阳模拟)在①{bn}为等比数列,b1=a1,3b2=a2,②{bn}为等差数列,2b1=a1,4b2=a2,③{bn}为等比数列,b1=a1+2,b2=a2+4这三个条件中任选一个,补充在下面的问题中,并解答.
又a1=2满足an=(2n-1)·2n,所以an=(2n-1)·2n.
若选①,设等比数列{bn}的公比为q(q≠0).
由已知得b1=2,b2=2q=4,则q=2,所以bn=2×2n-1=2n.
由Sk=k2≥2 020,k∈N*,可得k≥45,所以存在正整数k,使得Sk≥2 020成立,且k的最小值为45.
若选②,设等差数列{bn}的公差为d.
由已知得b1=1,b2=3,则d=b2-b1=2,
由Sk=2k+1-2≥2 020,k∈N*得k≥10,所以存在正整数k,使得Sk≥2 020成立,且k的最小值为10.
若选③,设等比数列{bn}的公比为q(q≠0).
数学思想·扩思路
函数与方程思想
(2021·江西南昌一中月考)在数列{an}中,a1=1,a1+2a2+3a3+…+nan=
an+1.
(1)求数列{an}的通项公式;
(2)若存在n∈N*,使得an≥(n+1)3nλ成立,求实数λ的最大值.
同课章节目录
