利用迭代函数解一类数列不等式问题课件(29张PPT)
文档属性
| 名称 | 利用迭代函数解一类数列不等式问题课件(29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 16:07:28 | ||
图片预览






文档简介
(共29张PPT)
利用迭代函数解一类数列不等式问题
杭州一模第22题
原题展示-如何上好一节习题课
一题多解,多个角度理解问题,深挖题目本身;
多题一解,提炼通性通法,拓展题目外延。
变式教学是习题课教学的重要模式。
本课以变式教学的形式展开设计,从一题多解、多题一解两个角度进行课题的设计。
第二问解法一:通法-数学归纳法
意图:方法展示,书写展示,希望规范学生书写过程
第二问解法二:迭代法
第二问解法三:参考答案法
课题引入:从学生的常规思维中遇到的阻碍入手
培养严密的数学思维,是数学核心素养培养的重要方面,从问题入手
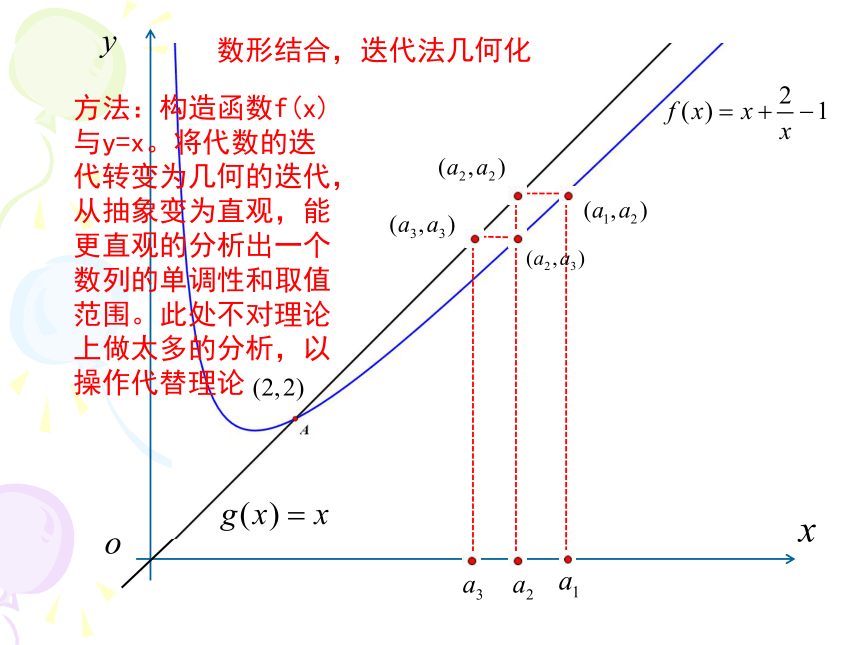
数形结合,迭代法几何化
方法:构造函数f(x)与y=x。将代数的迭代转变为几何的迭代,从抽象变为直观,能更直观的分析出一个数列的单调性和取值范围。此处不对理论上做太多的分析,以操作代替理论
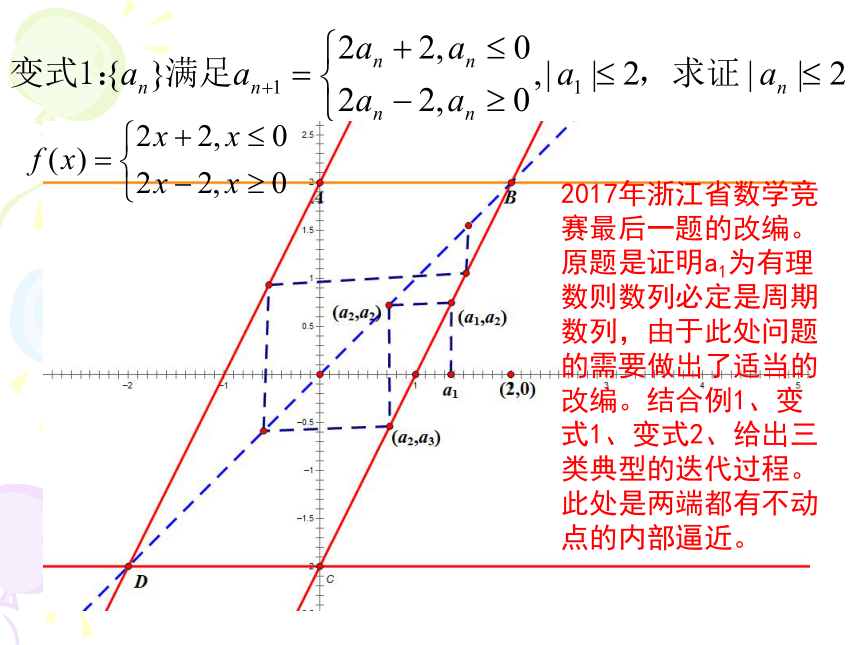
2017年浙江省数学竞赛最后一题的改编。原题是证明a1为有理数则数列必定是周期数列,由于此处问题的需要做出了适当的改编。结合例1、变式1、变式2、给出三类典型的迭代过程。此处是两端都有不动点的内部逼近。
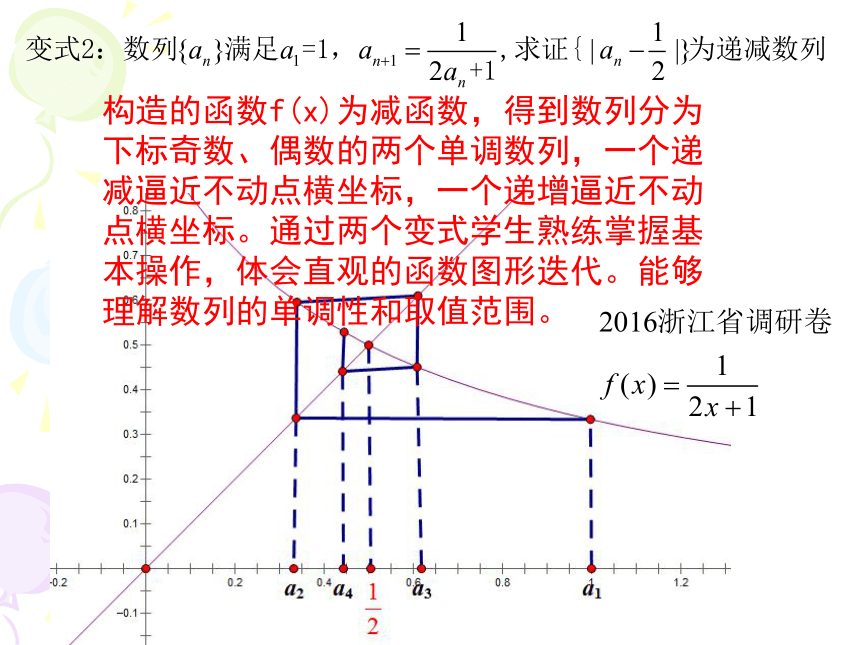
构造的函数f(x)为减函数,得到数列分为下标奇数、偶数的两个单调数列,一个递减逼近不动点横坐标,一个递增逼近不动点横坐标。通过两个变式学生熟练掌握基本操作,体会直观的函数图形迭代。能够理解数列的单调性和取值范围。
原理解释:
必然成立
从代数的形式,解释必然性的原因。学生对代数的推导能力较差,所以不得已只能自己给出证明。
分析答案,进一步引起冲突,希望学生有所思考,希望学生能在思维上有所提升
不仅仅是等比型,还是两点连线的斜率,可以利用导数的概念,求出斜率的取值范围
学生自主完成代数到几何的转换,强化数形结合分析问题的能力!
2015年浙江省高考题第一问,变式训练强化思维。需要学生能理解图像的本质,从图中理解证明结论的合理性。
设计意图:需要在理解本质的基础上,进一步提高数形结合的思维,将显然的图形结果表述成严谨的代数过程,熟练图形的操作过程,熟练代数的书写过程。
迭代过程图
斜率变化图
解:
利用迭代函数理解数列变化的本质
类型2
利用图像可快速的得到取值范围和斜率的范围,从而易得
此处的裂项怎么理解?
这就是想到裂项的原因,因为符合,所以进行,学生需要理解裂项的依据
分析:第一问具体的计算,可通过图像理解数列的单调性和取值范围,发现是单调递增,且无上界。
第二问对于幂指数是指数型,我们可分析为取对数型的放缩问题。
我们这里来分析Bn的求和问题
总结:
问题的遗憾
1.f(x)=x无解的类型没有好的方法进行分析
2.数列为无上界的递增,不能很精确的找到逼近的范围
3.此法只使用于多项式型的效果,因为对数、指数不易因式分解
利用迭代函数解一类数列不等式问题
杭州一模第22题
原题展示-如何上好一节习题课
一题多解,多个角度理解问题,深挖题目本身;
多题一解,提炼通性通法,拓展题目外延。
变式教学是习题课教学的重要模式。
本课以变式教学的形式展开设计,从一题多解、多题一解两个角度进行课题的设计。
第二问解法一:通法-数学归纳法
意图:方法展示,书写展示,希望规范学生书写过程
第二问解法二:迭代法
第二问解法三:参考答案法
课题引入:从学生的常规思维中遇到的阻碍入手
培养严密的数学思维,是数学核心素养培养的重要方面,从问题入手
数形结合,迭代法几何化
方法:构造函数f(x)与y=x。将代数的迭代转变为几何的迭代,从抽象变为直观,能更直观的分析出一个数列的单调性和取值范围。此处不对理论上做太多的分析,以操作代替理论
2017年浙江省数学竞赛最后一题的改编。原题是证明a1为有理数则数列必定是周期数列,由于此处问题的需要做出了适当的改编。结合例1、变式1、变式2、给出三类典型的迭代过程。此处是两端都有不动点的内部逼近。
构造的函数f(x)为减函数,得到数列分为下标奇数、偶数的两个单调数列,一个递减逼近不动点横坐标,一个递增逼近不动点横坐标。通过两个变式学生熟练掌握基本操作,体会直观的函数图形迭代。能够理解数列的单调性和取值范围。
原理解释:
必然成立
从代数的形式,解释必然性的原因。学生对代数的推导能力较差,所以不得已只能自己给出证明。
分析答案,进一步引起冲突,希望学生有所思考,希望学生能在思维上有所提升
不仅仅是等比型,还是两点连线的斜率,可以利用导数的概念,求出斜率的取值范围
学生自主完成代数到几何的转换,强化数形结合分析问题的能力!
2015年浙江省高考题第一问,变式训练强化思维。需要学生能理解图像的本质,从图中理解证明结论的合理性。
设计意图:需要在理解本质的基础上,进一步提高数形结合的思维,将显然的图形结果表述成严谨的代数过程,熟练图形的操作过程,熟练代数的书写过程。
迭代过程图
斜率变化图
解:
利用迭代函数理解数列变化的本质
类型2
利用图像可快速的得到取值范围和斜率的范围,从而易得
此处的裂项怎么理解?
这就是想到裂项的原因,因为符合,所以进行,学生需要理解裂项的依据
分析:第一问具体的计算,可通过图像理解数列的单调性和取值范围,发现是单调递增,且无上界。
第二问对于幂指数是指数型,我们可分析为取对数型的放缩问题。
我们这里来分析Bn的求和问题
总结:
问题的遗憾
1.f(x)=x无解的类型没有好的方法进行分析
2.数列为无上界的递增,不能很精确的找到逼近的范围
3.此法只使用于多项式型的效果,因为对数、指数不易因式分解
同课章节目录
