2021-2022学年北师大版九年级数学下册2.2二次函数的图象与性质同步测试(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册2.2二次函数的图象与性质同步测试(Word版,附答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 395.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 08:25:04 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学下册《2.2二次函数的图象与性质》同步测试(附答案)
一.选择题(共10小题,满分30分)
1.已知点A(1,y1),B(2,y2)在抛物线y=﹣(x+1)2+2上,则下列结论正确的是( )
A.2>y1>y2 B.2>y2>y1 C.y1>y2>2 D.y2>y1>2
2.将抛物线y=﹣5x2+1向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为( )
A.y=﹣5(x+1)2﹣1 B.y=﹣5(x﹣1)2﹣1
C.y=﹣5(x+1)2+3 D.y=﹣5(x﹣1)2+3
3.若抛物线y=﹣x2+bx+c经过点(﹣2,3),则2c﹣4b﹣9的值是( )
A.5 B.﹣1 C.4 D.18
4.已知抛物线y=ax2+bx+c的图象如图所示,则|a﹣b+c|+|2a+b|=( )
A.a+b B.a﹣2b C.a﹣b D.3a
5.如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( )
A.abc<0 B.2a+b<0 C.a﹣b+c<0 D.4ac﹣b2<0
6.抛物线y=x2+2x+3的对称轴是( )
A.直线x=1 B.直线x=﹣1 C.直线x=﹣2 D.直线x=2
7.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0.其中正确的是( )
A.①④ B.②④ C.①②③ D.①②③④
8.一次函数y=ax+c(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
9.二次函数y=﹣(x﹣1)2+5,当m≤x≤n且mn<0时,y的最小值为2m,最大值为2n,则m+n的值为( )
A. B.2 C. D.
10.如图是抛物线y=ax2+bx+c图象的一部分,且抛物线的对称轴为x=﹣1,那么下列说法正确的是( )
①b2>4ac;②abc>0;③2a+b=0;④a+b+c>0;⑤a﹣b+c<0.
A.①②③④ B.②④⑤ C.②③④ D.①④⑤
二.填空题(共10小题,满分40分)
11.如图,抛物线y=ax2+bx+c(a≠0)过点(﹣1,0),(0,2),且顶点在第一象限,设M=4a+2b+c,则M的取值范围是 .
12.如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,下列结论中:
①abc<0;②9a﹣3b+c<0;③b2﹣4ac>0;④a>b,
正确的结论是 (只填序号).
13.如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=﹣x2+6x上一点,且在x轴上方,则△BCD面积的最大值为 .
14.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,则下列结论:①abc<0;②;③ac﹣b+1=0;④OA OB=﹣.其中正确结论的序号是 .
15.将抛物线y=x2+4x+3绕原点旋转180°后,再分别向下、向右平移3个单位,此时该抛物线的解析式为 .
16.已知抛物线y=ax2﹣x+1(a≠0)与线段AB有两个不同的交点,已知A(﹣1,0),B(1,1),则a的取值范围是 .
17.已知a、b、m满足a+2b=m2﹣6m﹣5,3a+4b=﹣m2+2m﹣6,则a+b的最大值为 .
18.已知点P(x,y)在二次函数y=2(x+1)2﹣3的图象上,当﹣2<x≤1时,y的取值范围是 .
19.已知抛物线y=﹣4x2+4mx﹣4m﹣m2(m是常数),若0≤x≤1时,函数y有最大值﹣5,则m的值为 .
20.二次函数y=x2﹣6x+c的图象的顶点与原点的距离为5,则c= .
三.解答题(共5小题,满分50分)
21.若二次函数的解析式为y=(x﹣m)(x﹣1)(1≤m≤2)
(1)当x分别取﹣1,0,1时对应的函数值为y1,y2,y3,请比较y1,y2,y3的大小关系.
(2)对于m,当x>k时,y随x的增大而增大,求k的最小整数值.
(3)若函数过(a,b)点和(a+6,b)点,求b的取值范围.
22.已知二次函数y=﹣x2+2mx﹣4m+2(m为常数)
(1)请你用m的代数式表示该函数的顶点坐标.
(2)对于二次函数y=﹣x2+2mx﹣4m+2,若当x≥1时,函数值y随x的增大而减小,请你求出m的取值范围.
(3)若二次函数y=﹣x2+2mx﹣4m+2的顶点纵坐标为H,写出H与m的函数关系式,并判断该函数图象的顶点是否有最高点(或最低点)?若有,请求出这个点的坐标.
23.已知二次函数y=ax2﹣4ax+3a.
(Ⅰ)求该二次函数的对称轴;
(Ⅱ)若该二次函数的图象开口向下,当1≤x≤4时,y的最大值是2,且当1≤x≤4时,函数图象的最高点为点P,最低点为点Q,求△OPQ的面积;
(Ⅲ)若二次函数的图象开口向下,对于该抛物线上的两点P(x1,y1),Q(x2,y2),当t≤x1≤t+1,x2≥5时,均满足y1≥y2,请结合图象,直接写出t的最大值.
24.已知函数y=(m为常数),此函数图象记为G.
(1)当m=时,
①当y=﹣1时,求图象G上对应点的坐标;
②当﹣1≤x≤2时,求y的取值范围.
(2)当m=1时,直线y=2k+1(k为常数)与图象G的交点中横坐标最小的交点在直线x=﹣1和x=1之间(不包括边界)时,求k的取值范围.
(3)当x>m时,图象G与坐标轴有两个交点,直接写出m的取值范围.
25.如图1,在平面直角坐标系中,点A的坐标为(1,﹣2),点B的坐标为(3,﹣1),二次函数y=﹣x2的图象为l1.
(1)平移抛物线l1,使平移后的抛物线过点A,但不过点B,写出平移后的抛物线的一个解析式(任写一个即可);
(2)平移抛物线l1,使平移后的抛物线过A、B两点,记抛物线为l2,如图2,求抛物线l2的函数解析式及顶点C的坐标;
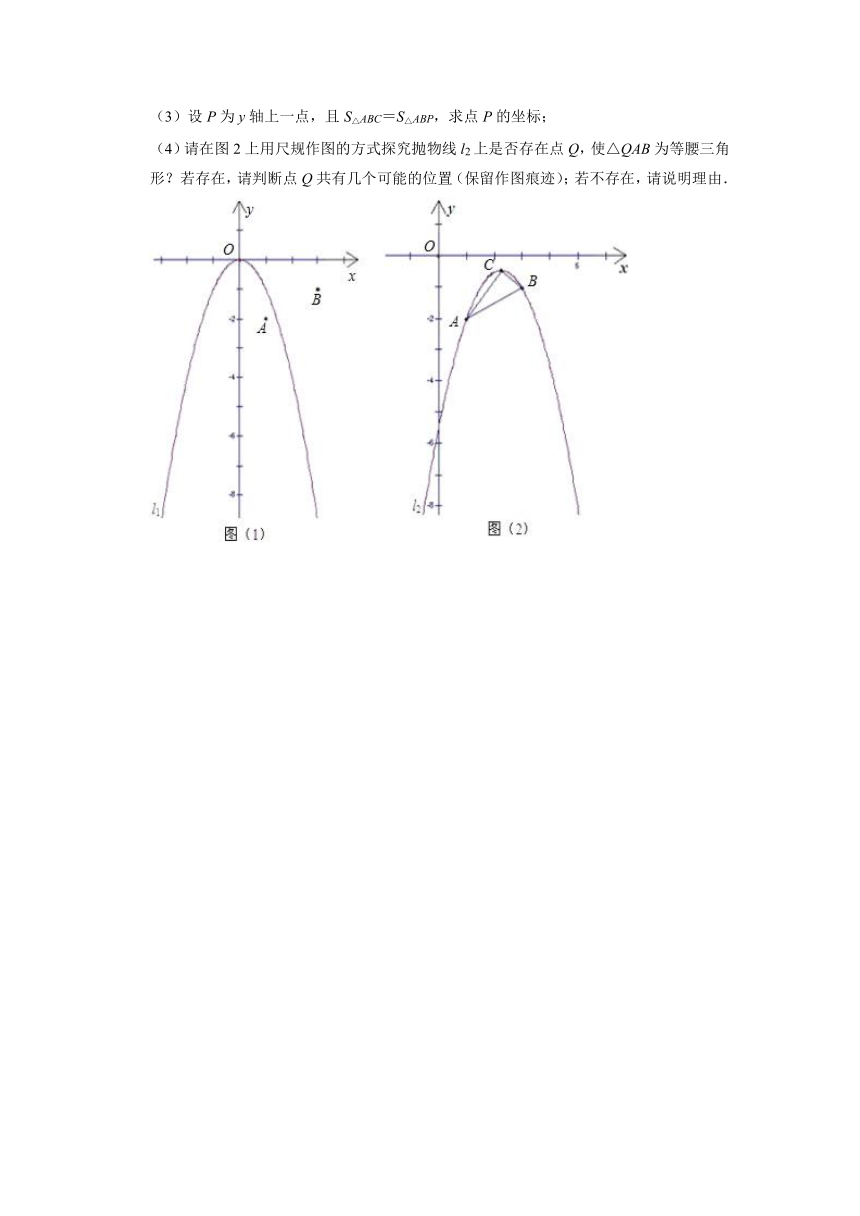
(3)设P为y轴上一点,且S△ABC=S△ABP,求点P的坐标;
(4)请在图2上用尺规作图的方式探究抛物线l2上是否存在点Q,使△QAB为等腰三角形?若存在,请判断点Q共有几个可能的位置(保留作图痕迹);若不存在,请说明理由.
参考答案
一.选择题(共10小题,满分30分)
1.解:当x=1时,y1=﹣(x+1)2+2=﹣(1+1)2+2=﹣2;
当x=2时,y1=﹣(x+1)2+2=﹣(2+1)2+2=﹣7;
所以2>y1>y2.
故选:A.
2.解:将抛物线y=﹣5x2+1向左平移1个单位长度,得到y=﹣5(x+1)2+1,再向下平移2个单位长度,
所得到的抛物线为:y=﹣5(x+1)2﹣1.
故选:A.
3.解:∵抛物线y=﹣x2+bx+c经过点(﹣2,3),
∴﹣(﹣2)2﹣2b+c=3,
整理得,﹣2b+c=7,
∴2c﹣4b﹣9=2(c﹣2b)﹣9=2×7﹣9=5,
故选:A.
4.解:观察函数图象,发现:
图象过原点,c=0;
抛物线开口向上,a>0;
抛物线的对称轴0<﹣<1,﹣2a<b<0.
∴|a﹣b+c|=a﹣b,|2a+b|=2a+b,
∴|a﹣b+c|+|2a+b|=a﹣b+2a+b=3a.
故选:D.
5.解:A、根据图示知,抛物线开口方向向上,则a>0.
抛物线的对称轴x=﹣=1>0,则b<0.
抛物线与y轴交与负半轴,则c<0,
所以abc>0.
故A选项错误;
B、∵x=﹣=1,
∴b=﹣2a,
∴2a+b=0.
故B选项错误;
C、∵对称轴为直线x=1,图象经过(3,0),
∴该抛物线与x轴的另一交点的坐标是(﹣1,0),
∴当x=﹣1时,y=0,即a﹣b+c=0.
故C选项错误;
D、根据图示知,该抛物线与x轴有两个不同的交点,则Δ=b2﹣4ac>0,则4ac﹣b2<0.
故D选项正确;
故选:D.
6.解:∵y=x2+2x+3=(x+1)2+2,
∴抛物线的对称轴为直线x=﹣1.
故选:B.
7.解:∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线x=﹣=1,
∴b=﹣2a<0,
∴ab<0,所以①正确;
∵抛物线与x轴有2个交点,
∴Δ=b2﹣4ac>0,所以②正确;
∵x=1时,y<0,
∴a+b+c<0,
而c<0,
∴a+b+2c<0,所以③正确;
∵抛物线的对称轴为直线x=﹣=1,
∴b=﹣2a,
而x=﹣1时,y>0,即a﹣b+c>0,
∴a+2a+c>0,所以④错误.
故选:C.
8.解:A、一次函数y=ax+c与y轴交点应为(0,c),二次函数y=ax2+bx+c与y轴交点也应为(0,c),图象不符合,故本选项错误;
B、由抛物线可知,a>0,由直线可知,a<0,a的取值矛盾,故本选项错误;
C、由抛物线可知,a<0,由直线可知,a>0,a的取值矛盾,故本选项错误;
D、由抛物线可知,a<0,由直线可知,a<0,且抛物线与直线与y轴的交点相同,故本选项正确.
故选:D.
9.解:二次函数y=﹣(x﹣1)2+5的大致图象如下:
.
①当m<0≤x≤n<1时,当x=m时y取最小值,即2m=﹣(m﹣1)2+5,
解得:m=﹣2或m=2(舍去).
当x=n时y取最大值,即2n=﹣(n﹣1)2+5,
解得:n=2或n=﹣2(均不合题意,舍去);
②当m<0≤x≤1<n时,当x=m时y取最小值,即2m=﹣(m﹣1)2+5,
解得:m=﹣2.
当x=1时y取最大值,即2n=﹣(1﹣1)2+5,
解得:n=,
③当m<0<x≤n时,x=n时y取最小值,x=1时y取最大值,
2m=﹣(n﹣1)2+5,n=,
∴m=,
∵m<0,
∴此种情形不合题意,
所以m+n=﹣2+=.
故选:D.
10.解:①由抛物线与x轴交于两点可知:b2﹣4ac>0,故①正确;
②由抛物线的图象可知:a>0,c<0,
对称轴<0,
∴b>0,
∴abc<0,故②错误;
③由对称轴可知:=﹣1,
∴b=2a,即2a﹣b=0,故③错误;
④当x=1时,y=a+b+c>0,
故④正确;
⑤当x=﹣1时,y=a﹣b+c<0,故⑤正确;
故选:D.
二.填空题(共10小题,满分40分)
11.解:将(﹣1,0)与(0,2)代入y=ax2+bx+c,
∴0=a﹣b+c,2=c,
∴b=a+2,
∵>0,a<0,
∴b>0,
∴a>﹣2,
∴﹣2<a<0,
∴M=4a+2(a+2)+2
=6a+6,
∴﹣6<M<6,
故答案为:﹣6<M<6;
12.解:∵抛物线开口向下
∴a<0,
∵对称轴为x=﹣1
∴=﹣1
∴b=2a<0,
∵抛物线与y轴交点在y轴正半轴
∴c>0
∴abc>0故①错误
∵由图象得x=﹣3时y<0
∴9a﹣3b+c<0 故②正确,
∵图象与x轴有两个交点
∴Δ=b2﹣4ac>0 故③正确
∵a﹣b=a﹣2a=﹣a>0
∴a>b故④正确
故答案为②③④
13.解:∵D是抛物线y=﹣x2+6x上一点,
∴设D(x,﹣x2+6x),
∵顶点C的坐标为(4,3),
∴OC==5,
∵四边形OABC是菱形,
∴BC=OC=5,BC∥x轴,
∴S△BCD=×5×(﹣x2+6x﹣3)=﹣(x﹣3)2+15,
∵﹣<0,
∴S△BCD有最大值,最大值为15,
故答案为15.
14.解:观察函数图象,发现:
开口向下 a<0;与y轴交点在y轴正半轴 c>0;对称轴在y轴右侧 ﹣>0;顶点在x轴上方 >0.
①∵a<0,c>0,﹣>0,
∴b>0,
∴abc<0,①成立;
②∵>0,
∴<0,②不成立;
③∵OA=OC,
∴xA=﹣c,
将点A(﹣c,0)代入y=ax2+bx+c中,
得:ac2﹣bc+c=0,即ac﹣b+1=0,③成立;
④∵OA=﹣xA,OB=xB,xA xB=,
∴OA OB=﹣,④成立.
综上可知:①③④成立.
故答案为:①③④.
15.解:y=x2+4x+3=(x+2)2﹣1.此时,该抛物线顶点坐标是(﹣2,﹣1).
将该抛物线绕坐标原点O旋转180°后的顶点坐标是(2,1).再分别向下、向右平移3个单位后的顶点坐标是(﹣1,﹣2).
所以此时抛物线的解析式为:y=﹣(x+1)2﹣2.
故答案是:y=﹣(x+1)2﹣2.
16.解:由点A、B的坐标得,直线AB的表达式为y=x+,
∵抛物线y=ax2﹣x+1(a≠0)与线段AB有两个不同的交点,
∴令x+=ax2﹣x+1,则2ax2﹣3x+1=0,
∴△=9﹣8a>0,
∴a<;
①当a<0时,
此时函数的对称轴在y轴左侧,
当抛物线过点A时,为两个函数有两个交点的临界点,
将点A的坐标代入抛物线表达式得:a+1+1=0,
解得a=﹣2,
故a≤﹣2;
②当a>0时,
此时函数的对称轴在y轴右侧,
当抛物线过点B时,为两个函数有两个交点的临界点,
将点B的坐标代入抛物线表达式得:a﹣1+1=1,
解得a=1,
即:a≥1
∴1≤a<
综上所述:1≤a<或a≤﹣2.
故答案为1≤a<或a≤﹣2.
17.解:,
②﹣①得:2a+2b=﹣2m2+8m﹣1,
∴a+b=﹣m2+4m﹣
=﹣(m﹣2)2+,
∴当m=2时,a+b有最大值,最大值为.
故答案为:.
18.解:∵二次函数y=2(x+1)2﹣3,
∴该函数对称轴是直线x=﹣1,当x=﹣1时,取得最小值,此时y=﹣3,
∵点P(x,y)在二次函数y=2(x+1)2﹣3的图象上,
∴当﹣2<x≤1时,y的取值范围是:﹣3≤y≤5,
故答案为:﹣3≤y≤5.
19.解:∵y=﹣4x2+4mx﹣4m﹣m2=﹣4(x﹣)2﹣4m,
∴抛物线开口向下,对称轴为直线x=.
当<0,即m<0时,x=0时y取最大值(如图1所示),
∴﹣4m﹣m2=﹣5,
解得:m1=﹣5,m2=1(不合题意,舍去);
当0≤≤1,即0≤m≤2时,x=时y取最大值(如图2所示),
∴﹣4m=﹣5,
解得:m3=;
当>1,即m>2时,x=1时y取最大值(如图3所示),
∴﹣4+4m﹣4m﹣m2=﹣5,
解得:m4=﹣1(不合题意,舍去),m5=1(不合题意,舍去).
综上所述,m的值为﹣5或.
故答案为:﹣5或.
20.解:∵二次函数y=x2﹣6x+c的图象的顶点坐标为(3,c﹣9),
∴32+(c﹣9)2=52,
解得c=13或c=5.
故答案为:13或5.
三.解答题(共5小题,满分50分)
21.解:(1)观察图象可知,x≤1时,y随x的增大而减小,
∵﹣1<0<1,
∴y1>y2>y3.
(2)观察图象可知k的最小整数为2.
(3)设直线y=b与抛物线的交点为(x1,b),(x2,b),
由题意x1﹣x2=6,
由,消去y得到,x2﹣(m+1)x+m﹣b=0,
∴x1+x2=m+1,x1x2=m﹣b,
∵(x1+x2)2﹣4x1x2=36,
∴(m+1)2﹣4(m﹣b)=36,
∴b=,
设y′=m2﹣2m,
∵y′=(m﹣1)2﹣1,
当1≤m≤2时,﹣1≤y′≤0,
∴≤b≤9.
22.解:(1)∵﹣=﹣=m,=m2﹣4m+2,
∴顶点坐标为:(m,m2﹣4m+2);
(2)∵抛物线的对称轴为:直线x=m,
∵a=﹣1<0,
∴当x≥m时,函数值y随x的增大而减小,
∵当x≥1时,函数值y随x的增大而减小,
∴m≤1;
(3)∵二次函数y=﹣x2+2mx﹣4m+2的顶点纵坐标为H,
∴H=m2﹣4m+2=(m﹣2)2﹣2,
∵1>0,
∴函数顶点有最低点,坐标为(2,﹣2).
23.解:(Ⅰ)对称轴x=﹣=2.
(Ⅱ)∵该二次函数的图象开口向下,且对称轴为直线x=2,
∴当x=2时,y取到在1≤x≤4上的最大值为2,即P(2,2),
∴4a﹣8a+3a=2,
∴a=﹣2,
∴y=﹣2x2+8x﹣6,
∵当1≤x≤2时,y随x的增大而增大,
∴当x=1时,y取到在1≤x≤2上的最小值0.
∵当2≤x≤4时,y随x的增大而减小,
∴当x=4时,y取到在2≤x≤4上的最小值﹣6.
∴当1≤x≤4时,y的最小值为﹣6,即Q(4,﹣6).
∴△OPQ的面积为4×(2+6)﹣2×2÷2﹣4×6÷2﹣(4﹣2)×(2+6)÷2=10;
(Ⅲ)∵当t≤x1≤t+1,x2≥5时,均满足y1≥y2,
∴当抛物线开口向下,点P在点Q左边或重合且在点Q关于对称轴对称点的右边时,满足条件,
∴t+1≤5且t≥﹣1,
∴﹣1≤t≤4,
∴t的最大值为4.
24.解:(1)当m=时,函数可化为y=,
①针对于函数y=x2﹣2x+2,
当y=﹣1时,x2﹣2x+2=﹣1,此方程无解;
针对于函数y=﹣x2+x+,
当y=﹣1时,﹣x2+x+=﹣1,
∴x=(舍)或x=﹣1,
∴当y=﹣1时,图象G上对应点的坐标为(﹣1,﹣1);
②画出函数图象如图1所示,
针对于函数y=﹣x2+x+,
当x=﹣1时,y=﹣1﹣+=﹣1,
当x=时,y=﹣+×+=,
针对于函数y=x2﹣2x+2,
当x=1时,y=1﹣2+2=1,
当x=2是,y=22﹣2×2+2=2,
∴当﹣1≤x≤2时,y的取值范围﹣1≤y≤或1≤y≤2;
(2)当m=1时,y=,
画出函数图象如图2所示,
针对于y=﹣x2+2x+2,
当x=﹣1时,y=﹣1,
当x=1时,y=3,
∵直线y=2k+1(k为常数)与图象G的交点中横坐标最小的交点在直线x=﹣1和x=1之间(不包括边界)时,
∴﹣1<2k+1<3,
∴﹣1<k<1;
(3)∵x>m,
∴只考虑函数y=x2﹣6mx+6m(x>m),
此函数的图象如图3所示,
∵函数的解析式为y=x2﹣6mx+6m(x>m),
∴此函数的对称轴为直线x=3m,
当m<0时,3m<m,图象如图3粉色线条,
∵图象与坐标轴有两个交点,
∴当x=m时,y=﹣5m2+6m=﹣m(5m﹣6)<0,
∴m<,即m<0,函数图象与坐标轴有两个交点,
当m=0时,y=x2(x>0),图象如图3蓝色线条,此时,图象与坐标轴没有交点,
当m>0时,函数y=x2﹣6mx+6m(x>m)的图象如图3所示的黑色线条,
∴3m>m,
∵图象与坐标轴有两个交点,
∴当x=m时,y=﹣5m2+6m=﹣m(5m﹣6)>0,
∴m<,
当x=3m时,y=﹣9m2+6m=﹣3m(3m﹣2)<0,
∴m>,
即<m<,函数图象与坐标轴有两个交点,
综上,m<0或<m<,函数图象与坐标轴有两个交点.
25.解:(1)让抛物线过点A,即把点A的坐标代入计算,得到,b+c=﹣1,不过点B,则把点B的坐标代入得到3b+c≠8,依此两个要求,随便找一个数即可.故平移后的抛物线的一个解析式y=﹣x2+2x﹣3或y=﹣x2+4x﹣5等(满足条件即可);
(2)设l2的解析式为y=﹣x2+bx+c,联立方程组,
解得:,则l2的解析式为y=﹣x2+x﹣.
点C的坐标为().
(3)如答图1,过点A、B、C三点分别作x轴的垂线,垂足分别为D、E、F,
则AD=2,CF=,BE=1,DE=2,DF=,FE=.
得:S△ABC=S梯形ABED﹣S梯形BCFE﹣S梯形ACFD=.
延长BA交y轴于点G,直线AB的解析式为y=x﹣,则点G的坐标为(0,),设点P的坐标为(0,h),
①当点P位于点G的下方时,,连接AP、BP,
则S△ABP=S△BPG﹣S△APG=﹣﹣h,又S△ABC=S△ABP=,得,点P的坐标为(0,).
②当点P位于点G的上方时,,同理,点P的坐标为(0,).
综上所述所求点P的坐标为(0,)或(0,)
(4)作图痕迹如答图2所示.
若AB为等腰三角形的腰,则分别以A、B为圆心,以AB长为半径画圆,交抛物线分别于Q1、Q2;
若AB为等腰三角形的底边,则作AB的垂直平分线,交抛物线分别于Q3、Q4,
由图可知,满足条件的点有Q1、Q2、Q3、Q4,共4个可能的位置
一.选择题(共10小题,满分30分)
1.已知点A(1,y1),B(2,y2)在抛物线y=﹣(x+1)2+2上,则下列结论正确的是( )
A.2>y1>y2 B.2>y2>y1 C.y1>y2>2 D.y2>y1>2
2.将抛物线y=﹣5x2+1向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为( )
A.y=﹣5(x+1)2﹣1 B.y=﹣5(x﹣1)2﹣1
C.y=﹣5(x+1)2+3 D.y=﹣5(x﹣1)2+3
3.若抛物线y=﹣x2+bx+c经过点(﹣2,3),则2c﹣4b﹣9的值是( )
A.5 B.﹣1 C.4 D.18
4.已知抛物线y=ax2+bx+c的图象如图所示,则|a﹣b+c|+|2a+b|=( )
A.a+b B.a﹣2b C.a﹣b D.3a
5.如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( )
A.abc<0 B.2a+b<0 C.a﹣b+c<0 D.4ac﹣b2<0
6.抛物线y=x2+2x+3的对称轴是( )
A.直线x=1 B.直线x=﹣1 C.直线x=﹣2 D.直线x=2
7.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0.其中正确的是( )
A.①④ B.②④ C.①②③ D.①②③④
8.一次函数y=ax+c(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
9.二次函数y=﹣(x﹣1)2+5,当m≤x≤n且mn<0时,y的最小值为2m,最大值为2n,则m+n的值为( )
A. B.2 C. D.
10.如图是抛物线y=ax2+bx+c图象的一部分,且抛物线的对称轴为x=﹣1,那么下列说法正确的是( )
①b2>4ac;②abc>0;③2a+b=0;④a+b+c>0;⑤a﹣b+c<0.
A.①②③④ B.②④⑤ C.②③④ D.①④⑤
二.填空题(共10小题,满分40分)
11.如图,抛物线y=ax2+bx+c(a≠0)过点(﹣1,0),(0,2),且顶点在第一象限,设M=4a+2b+c,则M的取值范围是 .
12.如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,下列结论中:
①abc<0;②9a﹣3b+c<0;③b2﹣4ac>0;④a>b,
正确的结论是 (只填序号).
13.如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=﹣x2+6x上一点,且在x轴上方,则△BCD面积的最大值为 .
14.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,则下列结论:①abc<0;②;③ac﹣b+1=0;④OA OB=﹣.其中正确结论的序号是 .
15.将抛物线y=x2+4x+3绕原点旋转180°后,再分别向下、向右平移3个单位,此时该抛物线的解析式为 .
16.已知抛物线y=ax2﹣x+1(a≠0)与线段AB有两个不同的交点,已知A(﹣1,0),B(1,1),则a的取值范围是 .
17.已知a、b、m满足a+2b=m2﹣6m﹣5,3a+4b=﹣m2+2m﹣6,则a+b的最大值为 .
18.已知点P(x,y)在二次函数y=2(x+1)2﹣3的图象上,当﹣2<x≤1时,y的取值范围是 .
19.已知抛物线y=﹣4x2+4mx﹣4m﹣m2(m是常数),若0≤x≤1时,函数y有最大值﹣5,则m的值为 .
20.二次函数y=x2﹣6x+c的图象的顶点与原点的距离为5,则c= .
三.解答题(共5小题,满分50分)
21.若二次函数的解析式为y=(x﹣m)(x﹣1)(1≤m≤2)
(1)当x分别取﹣1,0,1时对应的函数值为y1,y2,y3,请比较y1,y2,y3的大小关系.
(2)对于m,当x>k时,y随x的增大而增大,求k的最小整数值.
(3)若函数过(a,b)点和(a+6,b)点,求b的取值范围.
22.已知二次函数y=﹣x2+2mx﹣4m+2(m为常数)
(1)请你用m的代数式表示该函数的顶点坐标.
(2)对于二次函数y=﹣x2+2mx﹣4m+2,若当x≥1时,函数值y随x的增大而减小,请你求出m的取值范围.
(3)若二次函数y=﹣x2+2mx﹣4m+2的顶点纵坐标为H,写出H与m的函数关系式,并判断该函数图象的顶点是否有最高点(或最低点)?若有,请求出这个点的坐标.
23.已知二次函数y=ax2﹣4ax+3a.
(Ⅰ)求该二次函数的对称轴;
(Ⅱ)若该二次函数的图象开口向下,当1≤x≤4时,y的最大值是2,且当1≤x≤4时,函数图象的最高点为点P,最低点为点Q,求△OPQ的面积;
(Ⅲ)若二次函数的图象开口向下,对于该抛物线上的两点P(x1,y1),Q(x2,y2),当t≤x1≤t+1,x2≥5时,均满足y1≥y2,请结合图象,直接写出t的最大值.
24.已知函数y=(m为常数),此函数图象记为G.
(1)当m=时,
①当y=﹣1时,求图象G上对应点的坐标;
②当﹣1≤x≤2时,求y的取值范围.
(2)当m=1时,直线y=2k+1(k为常数)与图象G的交点中横坐标最小的交点在直线x=﹣1和x=1之间(不包括边界)时,求k的取值范围.
(3)当x>m时,图象G与坐标轴有两个交点,直接写出m的取值范围.
25.如图1,在平面直角坐标系中,点A的坐标为(1,﹣2),点B的坐标为(3,﹣1),二次函数y=﹣x2的图象为l1.
(1)平移抛物线l1,使平移后的抛物线过点A,但不过点B,写出平移后的抛物线的一个解析式(任写一个即可);
(2)平移抛物线l1,使平移后的抛物线过A、B两点,记抛物线为l2,如图2,求抛物线l2的函数解析式及顶点C的坐标;
(3)设P为y轴上一点,且S△ABC=S△ABP,求点P的坐标;
(4)请在图2上用尺规作图的方式探究抛物线l2上是否存在点Q,使△QAB为等腰三角形?若存在,请判断点Q共有几个可能的位置(保留作图痕迹);若不存在,请说明理由.
参考答案
一.选择题(共10小题,满分30分)
1.解:当x=1时,y1=﹣(x+1)2+2=﹣(1+1)2+2=﹣2;
当x=2时,y1=﹣(x+1)2+2=﹣(2+1)2+2=﹣7;
所以2>y1>y2.
故选:A.
2.解:将抛物线y=﹣5x2+1向左平移1个单位长度,得到y=﹣5(x+1)2+1,再向下平移2个单位长度,
所得到的抛物线为:y=﹣5(x+1)2﹣1.
故选:A.
3.解:∵抛物线y=﹣x2+bx+c经过点(﹣2,3),
∴﹣(﹣2)2﹣2b+c=3,
整理得,﹣2b+c=7,
∴2c﹣4b﹣9=2(c﹣2b)﹣9=2×7﹣9=5,
故选:A.
4.解:观察函数图象,发现:
图象过原点,c=0;
抛物线开口向上,a>0;
抛物线的对称轴0<﹣<1,﹣2a<b<0.
∴|a﹣b+c|=a﹣b,|2a+b|=2a+b,
∴|a﹣b+c|+|2a+b|=a﹣b+2a+b=3a.
故选:D.
5.解:A、根据图示知,抛物线开口方向向上,则a>0.
抛物线的对称轴x=﹣=1>0,则b<0.
抛物线与y轴交与负半轴,则c<0,
所以abc>0.
故A选项错误;
B、∵x=﹣=1,
∴b=﹣2a,
∴2a+b=0.
故B选项错误;
C、∵对称轴为直线x=1,图象经过(3,0),
∴该抛物线与x轴的另一交点的坐标是(﹣1,0),
∴当x=﹣1时,y=0,即a﹣b+c=0.
故C选项错误;
D、根据图示知,该抛物线与x轴有两个不同的交点,则Δ=b2﹣4ac>0,则4ac﹣b2<0.
故D选项正确;
故选:D.
6.解:∵y=x2+2x+3=(x+1)2+2,
∴抛物线的对称轴为直线x=﹣1.
故选:B.
7.解:∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线x=﹣=1,
∴b=﹣2a<0,
∴ab<0,所以①正确;
∵抛物线与x轴有2个交点,
∴Δ=b2﹣4ac>0,所以②正确;
∵x=1时,y<0,
∴a+b+c<0,
而c<0,
∴a+b+2c<0,所以③正确;
∵抛物线的对称轴为直线x=﹣=1,
∴b=﹣2a,
而x=﹣1时,y>0,即a﹣b+c>0,
∴a+2a+c>0,所以④错误.
故选:C.
8.解:A、一次函数y=ax+c与y轴交点应为(0,c),二次函数y=ax2+bx+c与y轴交点也应为(0,c),图象不符合,故本选项错误;
B、由抛物线可知,a>0,由直线可知,a<0,a的取值矛盾,故本选项错误;
C、由抛物线可知,a<0,由直线可知,a>0,a的取值矛盾,故本选项错误;
D、由抛物线可知,a<0,由直线可知,a<0,且抛物线与直线与y轴的交点相同,故本选项正确.
故选:D.
9.解:二次函数y=﹣(x﹣1)2+5的大致图象如下:
.
①当m<0≤x≤n<1时,当x=m时y取最小值,即2m=﹣(m﹣1)2+5,
解得:m=﹣2或m=2(舍去).
当x=n时y取最大值,即2n=﹣(n﹣1)2+5,
解得:n=2或n=﹣2(均不合题意,舍去);
②当m<0≤x≤1<n时,当x=m时y取最小值,即2m=﹣(m﹣1)2+5,
解得:m=﹣2.
当x=1时y取最大值,即2n=﹣(1﹣1)2+5,
解得:n=,
③当m<0<x≤n时,x=n时y取最小值,x=1时y取最大值,
2m=﹣(n﹣1)2+5,n=,
∴m=,
∵m<0,
∴此种情形不合题意,
所以m+n=﹣2+=.
故选:D.
10.解:①由抛物线与x轴交于两点可知:b2﹣4ac>0,故①正确;
②由抛物线的图象可知:a>0,c<0,
对称轴<0,
∴b>0,
∴abc<0,故②错误;
③由对称轴可知:=﹣1,
∴b=2a,即2a﹣b=0,故③错误;
④当x=1时,y=a+b+c>0,
故④正确;
⑤当x=﹣1时,y=a﹣b+c<0,故⑤正确;
故选:D.
二.填空题(共10小题,满分40分)
11.解:将(﹣1,0)与(0,2)代入y=ax2+bx+c,
∴0=a﹣b+c,2=c,
∴b=a+2,
∵>0,a<0,
∴b>0,
∴a>﹣2,
∴﹣2<a<0,
∴M=4a+2(a+2)+2
=6a+6,
∴﹣6<M<6,
故答案为:﹣6<M<6;
12.解:∵抛物线开口向下
∴a<0,
∵对称轴为x=﹣1
∴=﹣1
∴b=2a<0,
∵抛物线与y轴交点在y轴正半轴
∴c>0
∴abc>0故①错误
∵由图象得x=﹣3时y<0
∴9a﹣3b+c<0 故②正确,
∵图象与x轴有两个交点
∴Δ=b2﹣4ac>0 故③正确
∵a﹣b=a﹣2a=﹣a>0
∴a>b故④正确
故答案为②③④
13.解:∵D是抛物线y=﹣x2+6x上一点,
∴设D(x,﹣x2+6x),
∵顶点C的坐标为(4,3),
∴OC==5,
∵四边形OABC是菱形,
∴BC=OC=5,BC∥x轴,
∴S△BCD=×5×(﹣x2+6x﹣3)=﹣(x﹣3)2+15,
∵﹣<0,
∴S△BCD有最大值,最大值为15,
故答案为15.
14.解:观察函数图象,发现:
开口向下 a<0;与y轴交点在y轴正半轴 c>0;对称轴在y轴右侧 ﹣>0;顶点在x轴上方 >0.
①∵a<0,c>0,﹣>0,
∴b>0,
∴abc<0,①成立;
②∵>0,
∴<0,②不成立;
③∵OA=OC,
∴xA=﹣c,
将点A(﹣c,0)代入y=ax2+bx+c中,
得:ac2﹣bc+c=0,即ac﹣b+1=0,③成立;
④∵OA=﹣xA,OB=xB,xA xB=,
∴OA OB=﹣,④成立.
综上可知:①③④成立.
故答案为:①③④.
15.解:y=x2+4x+3=(x+2)2﹣1.此时,该抛物线顶点坐标是(﹣2,﹣1).
将该抛物线绕坐标原点O旋转180°后的顶点坐标是(2,1).再分别向下、向右平移3个单位后的顶点坐标是(﹣1,﹣2).
所以此时抛物线的解析式为:y=﹣(x+1)2﹣2.
故答案是:y=﹣(x+1)2﹣2.
16.解:由点A、B的坐标得,直线AB的表达式为y=x+,
∵抛物线y=ax2﹣x+1(a≠0)与线段AB有两个不同的交点,
∴令x+=ax2﹣x+1,则2ax2﹣3x+1=0,
∴△=9﹣8a>0,
∴a<;
①当a<0时,
此时函数的对称轴在y轴左侧,
当抛物线过点A时,为两个函数有两个交点的临界点,
将点A的坐标代入抛物线表达式得:a+1+1=0,
解得a=﹣2,
故a≤﹣2;
②当a>0时,
此时函数的对称轴在y轴右侧,
当抛物线过点B时,为两个函数有两个交点的临界点,
将点B的坐标代入抛物线表达式得:a﹣1+1=1,
解得a=1,
即:a≥1
∴1≤a<
综上所述:1≤a<或a≤﹣2.
故答案为1≤a<或a≤﹣2.
17.解:,
②﹣①得:2a+2b=﹣2m2+8m﹣1,
∴a+b=﹣m2+4m﹣
=﹣(m﹣2)2+,
∴当m=2时,a+b有最大值,最大值为.
故答案为:.
18.解:∵二次函数y=2(x+1)2﹣3,
∴该函数对称轴是直线x=﹣1,当x=﹣1时,取得最小值,此时y=﹣3,
∵点P(x,y)在二次函数y=2(x+1)2﹣3的图象上,
∴当﹣2<x≤1时,y的取值范围是:﹣3≤y≤5,
故答案为:﹣3≤y≤5.
19.解:∵y=﹣4x2+4mx﹣4m﹣m2=﹣4(x﹣)2﹣4m,
∴抛物线开口向下,对称轴为直线x=.
当<0,即m<0时,x=0时y取最大值(如图1所示),
∴﹣4m﹣m2=﹣5,
解得:m1=﹣5,m2=1(不合题意,舍去);
当0≤≤1,即0≤m≤2时,x=时y取最大值(如图2所示),
∴﹣4m=﹣5,
解得:m3=;
当>1,即m>2时,x=1时y取最大值(如图3所示),
∴﹣4+4m﹣4m﹣m2=﹣5,
解得:m4=﹣1(不合题意,舍去),m5=1(不合题意,舍去).
综上所述,m的值为﹣5或.
故答案为:﹣5或.
20.解:∵二次函数y=x2﹣6x+c的图象的顶点坐标为(3,c﹣9),
∴32+(c﹣9)2=52,
解得c=13或c=5.
故答案为:13或5.
三.解答题(共5小题,满分50分)
21.解:(1)观察图象可知,x≤1时,y随x的增大而减小,
∵﹣1<0<1,
∴y1>y2>y3.
(2)观察图象可知k的最小整数为2.
(3)设直线y=b与抛物线的交点为(x1,b),(x2,b),
由题意x1﹣x2=6,
由,消去y得到,x2﹣(m+1)x+m﹣b=0,
∴x1+x2=m+1,x1x2=m﹣b,
∵(x1+x2)2﹣4x1x2=36,
∴(m+1)2﹣4(m﹣b)=36,
∴b=,
设y′=m2﹣2m,
∵y′=(m﹣1)2﹣1,
当1≤m≤2时,﹣1≤y′≤0,
∴≤b≤9.
22.解:(1)∵﹣=﹣=m,=m2﹣4m+2,
∴顶点坐标为:(m,m2﹣4m+2);
(2)∵抛物线的对称轴为:直线x=m,
∵a=﹣1<0,
∴当x≥m时,函数值y随x的增大而减小,
∵当x≥1时,函数值y随x的增大而减小,
∴m≤1;
(3)∵二次函数y=﹣x2+2mx﹣4m+2的顶点纵坐标为H,
∴H=m2﹣4m+2=(m﹣2)2﹣2,
∵1>0,
∴函数顶点有最低点,坐标为(2,﹣2).
23.解:(Ⅰ)对称轴x=﹣=2.
(Ⅱ)∵该二次函数的图象开口向下,且对称轴为直线x=2,
∴当x=2时,y取到在1≤x≤4上的最大值为2,即P(2,2),
∴4a﹣8a+3a=2,
∴a=﹣2,
∴y=﹣2x2+8x﹣6,
∵当1≤x≤2时,y随x的增大而增大,
∴当x=1时,y取到在1≤x≤2上的最小值0.
∵当2≤x≤4时,y随x的增大而减小,
∴当x=4时,y取到在2≤x≤4上的最小值﹣6.
∴当1≤x≤4时,y的最小值为﹣6,即Q(4,﹣6).
∴△OPQ的面积为4×(2+6)﹣2×2÷2﹣4×6÷2﹣(4﹣2)×(2+6)÷2=10;
(Ⅲ)∵当t≤x1≤t+1,x2≥5时,均满足y1≥y2,
∴当抛物线开口向下,点P在点Q左边或重合且在点Q关于对称轴对称点的右边时,满足条件,
∴t+1≤5且t≥﹣1,
∴﹣1≤t≤4,
∴t的最大值为4.
24.解:(1)当m=时,函数可化为y=,
①针对于函数y=x2﹣2x+2,
当y=﹣1时,x2﹣2x+2=﹣1,此方程无解;
针对于函数y=﹣x2+x+,
当y=﹣1时,﹣x2+x+=﹣1,
∴x=(舍)或x=﹣1,
∴当y=﹣1时,图象G上对应点的坐标为(﹣1,﹣1);
②画出函数图象如图1所示,
针对于函数y=﹣x2+x+,
当x=﹣1时,y=﹣1﹣+=﹣1,
当x=时,y=﹣+×+=,
针对于函数y=x2﹣2x+2,
当x=1时,y=1﹣2+2=1,
当x=2是,y=22﹣2×2+2=2,
∴当﹣1≤x≤2时,y的取值范围﹣1≤y≤或1≤y≤2;
(2)当m=1时,y=,
画出函数图象如图2所示,
针对于y=﹣x2+2x+2,
当x=﹣1时,y=﹣1,
当x=1时,y=3,
∵直线y=2k+1(k为常数)与图象G的交点中横坐标最小的交点在直线x=﹣1和x=1之间(不包括边界)时,
∴﹣1<2k+1<3,
∴﹣1<k<1;
(3)∵x>m,
∴只考虑函数y=x2﹣6mx+6m(x>m),
此函数的图象如图3所示,
∵函数的解析式为y=x2﹣6mx+6m(x>m),
∴此函数的对称轴为直线x=3m,
当m<0时,3m<m,图象如图3粉色线条,
∵图象与坐标轴有两个交点,
∴当x=m时,y=﹣5m2+6m=﹣m(5m﹣6)<0,
∴m<,即m<0,函数图象与坐标轴有两个交点,
当m=0时,y=x2(x>0),图象如图3蓝色线条,此时,图象与坐标轴没有交点,
当m>0时,函数y=x2﹣6mx+6m(x>m)的图象如图3所示的黑色线条,
∴3m>m,
∵图象与坐标轴有两个交点,
∴当x=m时,y=﹣5m2+6m=﹣m(5m﹣6)>0,
∴m<,
当x=3m时,y=﹣9m2+6m=﹣3m(3m﹣2)<0,
∴m>,
即<m<,函数图象与坐标轴有两个交点,
综上,m<0或<m<,函数图象与坐标轴有两个交点.
25.解:(1)让抛物线过点A,即把点A的坐标代入计算,得到,b+c=﹣1,不过点B,则把点B的坐标代入得到3b+c≠8,依此两个要求,随便找一个数即可.故平移后的抛物线的一个解析式y=﹣x2+2x﹣3或y=﹣x2+4x﹣5等(满足条件即可);
(2)设l2的解析式为y=﹣x2+bx+c,联立方程组,
解得:,则l2的解析式为y=﹣x2+x﹣.
点C的坐标为().
(3)如答图1,过点A、B、C三点分别作x轴的垂线,垂足分别为D、E、F,
则AD=2,CF=,BE=1,DE=2,DF=,FE=.
得:S△ABC=S梯形ABED﹣S梯形BCFE﹣S梯形ACFD=.
延长BA交y轴于点G,直线AB的解析式为y=x﹣,则点G的坐标为(0,),设点P的坐标为(0,h),
①当点P位于点G的下方时,,连接AP、BP,
则S△ABP=S△BPG﹣S△APG=﹣﹣h,又S△ABC=S△ABP=,得,点P的坐标为(0,).
②当点P位于点G的上方时,,同理,点P的坐标为(0,).
综上所述所求点P的坐标为(0,)或(0,)
(4)作图痕迹如答图2所示.
若AB为等腰三角形的腰,则分别以A、B为圆心,以AB长为半径画圆,交抛物线分别于Q1、Q2;
若AB为等腰三角形的底边,则作AB的垂直平分线,交抛物线分别于Q3、Q4,
由图可知,满足条件的点有Q1、Q2、Q3、Q4,共4个可能的位置
