2021-2022学年度北师大版九年级数学下册课件 2.2二次函数的图象与性质(第三课时)(共14张ppt)
文档属性
| 名称 | 2021-2022学年度北师大版九年级数学下册课件 2.2二次函数的图象与性质(第三课时)(共14张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 623.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 21:01:47 | ||
图片预览






文档简介
(共14张PPT)
2.2二次函数的图象与性质(第三课时)
知识回顾应用
1.指出下列二次函数的开口方向、对称轴和顶点坐标。
(1) y=2(x-3)2 -5
(2)y= -0.5(x+1)2
(3) y = 3(x+4)2+2
2.它们分别可以看成是由哪个函数图象通过怎样的平移得到。
函数y=ax +bx+c的图象
我们知道,作出二次函数y=3x2的图象,通过平移抛物线y=3x2可以得到二次函数y=3x2-6x+5的图象.
那是怎样的平移呢?
y=3x2-6x+5
y=3(x-1)2+2
只要将表达式右边进行配方就可以知道了。
配方后的表达式通常称为配方式或顶点式
函数y=ax +bx+c的顶点式
这个结果通常称为求顶点坐标公式.
顶点坐标公式
因此,二次函数y=ax +bx+c的图象是一条抛物线.
根据公式确定下列二次函数图象的对称轴和顶点坐标:
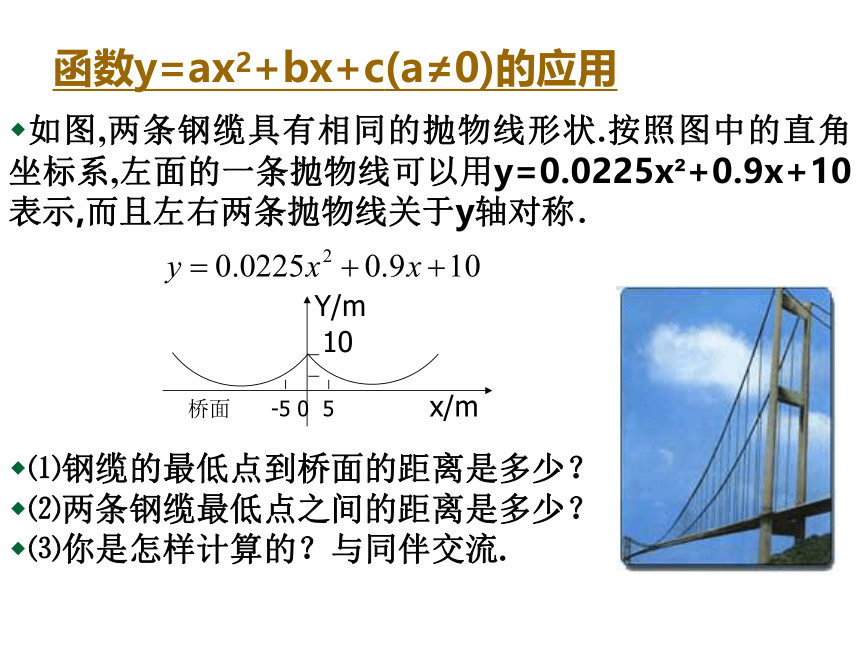
如图,两条钢缆具有相同的抛物线形状.按照图中的直角坐标系,左面的一条抛物线可以用y=0.0225x +0.9x+10表示,而且左右两条抛物线关于y轴对称.
⑴钢缆的最低点到桥面的距离是多少?
⑵两条钢缆最低点之间的距离是多少?
⑶你是怎样计算的?与同伴交流.
函数y=ax2+bx+c(a≠0)的应用
Y/m
x/m
桥面 -5 0 5
10
⑴.钢缆的最低点到桥面的距离是少?你是怎样计算的?与同伴交流.
可以将函数y=0.0225x2+0.9x+10配方,求得顶点坐标,从而获得钢缆的最低点到桥面的距离;
Y/m
x/m
桥面 -5 0 5
10
由此可知钢缆的最低点到桥面的距离是1m。
⑵两条钢缆最低点之间的距离是多少?你是怎样计算的?与同伴交流.
想一想,你知道图中右面钢缆的表达式是什么吗
Y/m
x/m
桥面 -5 0 5
10
⑶你还有其它方法吗?与同伴交流.
直接利用顶点坐标公式再计算一下上面问题中钢缆的最低点到桥面的距离以及两条钢缆最低点之间的距离.
Y/m
x/m
桥面 -5 0 5
10
由此可知钢缆的最低点
到桥面的距离是1m。
请你总结函数
函数y=ax2+bx+c(a≠0)
的图象和性质
想一想,函数y=ax2+bx+c和y=ax2的图象之间的关系是什么?
二次函数y=ax2+bx+c(a≠0)的图象和性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
由a,b和c的符号确定
由a,b和c的符号确定
向上
向下
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
根据图形填表:
1.相同点: (1)形状相同(图像都是抛物线,开口方向相同).
(2)都是轴对称图形.
(3)都有最(大或小)值.
(4)a>0时, 开口向上,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随 x的增大而增大. a<0时,开口向下,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随 x的增大而减小 .
2.不同点: (1)位置不同(2)顶点不同:分别是 和(0,0).
(3)对称轴不同:分别是 和y轴.
(4)最值不同:分别是 和0.
3.联系: y=a(x-h) +k(a≠0) 的图象可以看成y=ax 的图象先沿x轴整体左(右)平移| |个单位,再沿对称轴整体上(下)平移| |个单位 (当 >0时向上平移;当 <0时,向下平移)得到的.
小结 拓展
回味无穷
二次函数y=ax2+bx+c(a≠0)与=ax 的关系
练习
确定下列二次函数的开口方向、对称轴和顶点坐标.
2.2二次函数的图象与性质(第三课时)
知识回顾应用
1.指出下列二次函数的开口方向、对称轴和顶点坐标。
(1) y=2(x-3)2 -5
(2)y= -0.5(x+1)2
(3) y = 3(x+4)2+2
2.它们分别可以看成是由哪个函数图象通过怎样的平移得到。
函数y=ax +bx+c的图象
我们知道,作出二次函数y=3x2的图象,通过平移抛物线y=3x2可以得到二次函数y=3x2-6x+5的图象.
那是怎样的平移呢?
y=3x2-6x+5
y=3(x-1)2+2
只要将表达式右边进行配方就可以知道了。
配方后的表达式通常称为配方式或顶点式
函数y=ax +bx+c的顶点式
这个结果通常称为求顶点坐标公式.
顶点坐标公式
因此,二次函数y=ax +bx+c的图象是一条抛物线.
根据公式确定下列二次函数图象的对称轴和顶点坐标:
如图,两条钢缆具有相同的抛物线形状.按照图中的直角坐标系,左面的一条抛物线可以用y=0.0225x +0.9x+10表示,而且左右两条抛物线关于y轴对称.
⑴钢缆的最低点到桥面的距离是多少?
⑵两条钢缆最低点之间的距离是多少?
⑶你是怎样计算的?与同伴交流.
函数y=ax2+bx+c(a≠0)的应用
Y/m
x/m
桥面 -5 0 5
10
⑴.钢缆的最低点到桥面的距离是少?你是怎样计算的?与同伴交流.
可以将函数y=0.0225x2+0.9x+10配方,求得顶点坐标,从而获得钢缆的最低点到桥面的距离;
Y/m
x/m
桥面 -5 0 5
10
由此可知钢缆的最低点到桥面的距离是1m。
⑵两条钢缆最低点之间的距离是多少?你是怎样计算的?与同伴交流.
想一想,你知道图中右面钢缆的表达式是什么吗
Y/m
x/m
桥面 -5 0 5
10
⑶你还有其它方法吗?与同伴交流.
直接利用顶点坐标公式再计算一下上面问题中钢缆的最低点到桥面的距离以及两条钢缆最低点之间的距离.
Y/m
x/m
桥面 -5 0 5
10
由此可知钢缆的最低点
到桥面的距离是1m。
请你总结函数
函数y=ax2+bx+c(a≠0)
的图象和性质
想一想,函数y=ax2+bx+c和y=ax2的图象之间的关系是什么?
二次函数y=ax2+bx+c(a≠0)的图象和性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
由a,b和c的符号确定
由a,b和c的符号确定
向上
向下
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
根据图形填表:
1.相同点: (1)形状相同(图像都是抛物线,开口方向相同).
(2)都是轴对称图形.
(3)都有最(大或小)值.
(4)a>0时, 开口向上,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随 x的增大而增大. a<0时,开口向下,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随 x的增大而减小 .
2.不同点: (1)位置不同(2)顶点不同:分别是 和(0,0).
(3)对称轴不同:分别是 和y轴.
(4)最值不同:分别是 和0.
3.联系: y=a(x-h) +k(a≠0) 的图象可以看成y=ax 的图象先沿x轴整体左(右)平移| |个单位,再沿对称轴整体上(下)平移| |个单位 (当 >0时向上平移;当 <0时,向下平移)得到的.
小结 拓展
回味无穷
二次函数y=ax2+bx+c(a≠0)与=ax 的关系
练习
确定下列二次函数的开口方向、对称轴和顶点坐标.
