初中数学北师大九年级下学期第三章 圆:与圆有关的三角形相似几种模型(含答案)
文档属性
| 名称 | 初中数学北师大九年级下学期第三章 圆:与圆有关的三角形相似几种模型(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 14:46:13 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
初中数学北师大九年级下学期第三章圆:不得不说的与圆有关的三角形相似几种模型
圆几乎是中考数学必考的压轴题型之一,因为与圆结合的图形形状有很多,比如三角形、四边形等基本图形。可见其综合性、灵活性非常高,值得我们深入细致的去学习和研究。今天我们再以三角形与圆相结合的题型,来进一步学习和探讨圆中有关三角形相似的问题。
我们知道在圆中随便相连就可以形成很多三角形,而圆是轴对称图形,有无数条对称轴,这就造成了圆的一些特殊性质,比如:
直径所对的圆周角为直角;
平分一般弦(不是直径)的直径垂直于弦;
圆的切线与过该点的半径垂直等。
因此,圆中有非常多的直角三角形,且圆中三角形的相似一般是直角三角形的相似。
这些相似包括:A字相似(平行、不平行);8字相似(平行、不平行)、摄影相似、母子相似等。
只有熟悉并熟练掌握了圆中有关三角形的相似模型,才能在考试中快速制胜!
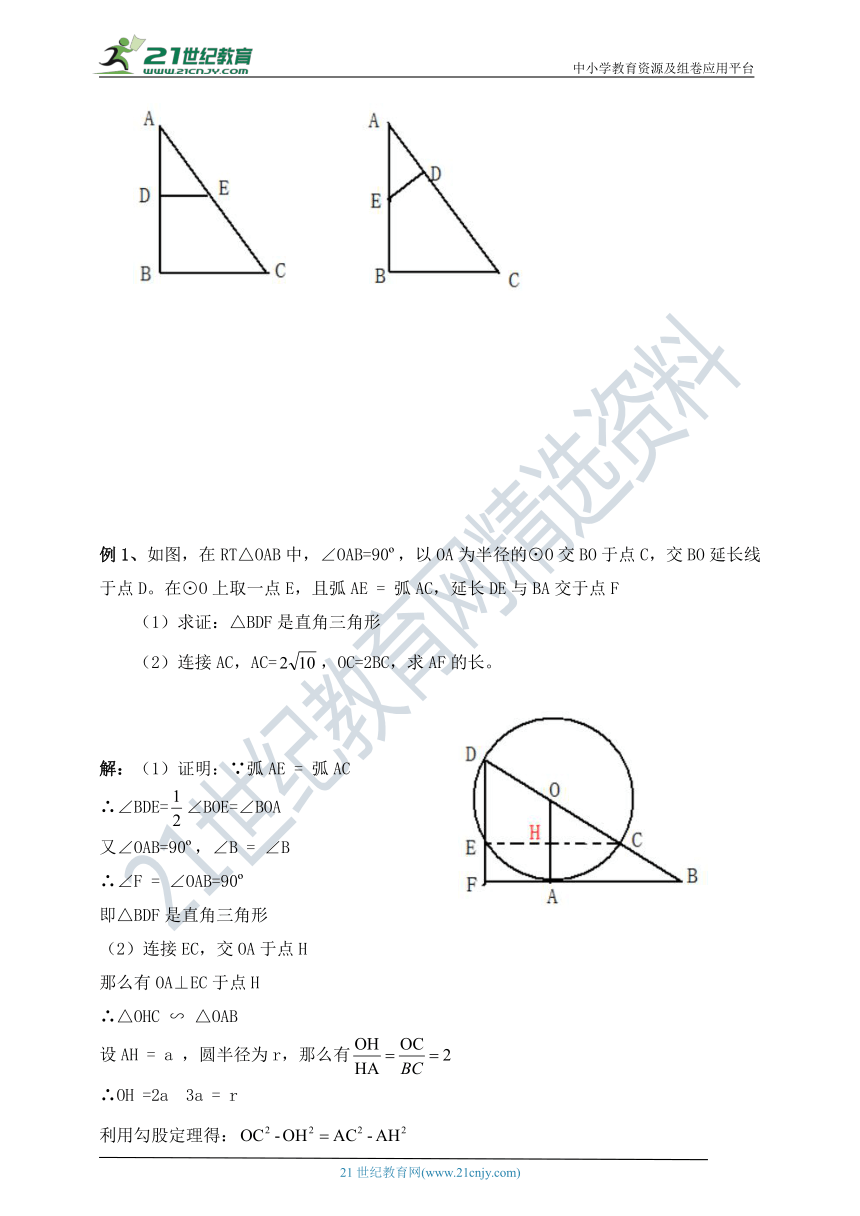
一、A字相似:包含平行与不平行两种
A字相似在圆中通常表现为直角三角形相似的形式:
例1、如图,在RT△OAB中,∠OAB=90 ,以OA为半径的⊙O交BO于点C,交BO延长线于点D。在⊙O上取一点E,且弧AE = 弧AC,延长DE与BA交于点F
求证:△BDF是直角三角形
连接AC,AC=,OC=2BC,求AF的长。
解:(1)证明:∵弧AE = 弧AC
∴∠BDE=∠BOE=∠BOA
又∠OAB=90 ,∠B = ∠B
∴∠F = ∠OAB=90
即△BDF是直角三角形
(2)连接EC,交OA于点H
那么有OA⊥EC于点H
∴△OHC ∽ △OAB
设AH = a ,圆半径为r,那么有
∴OH =2a 3a = r
利用勾股定理得:
即; 解得a=
∴AF = EH = CH =
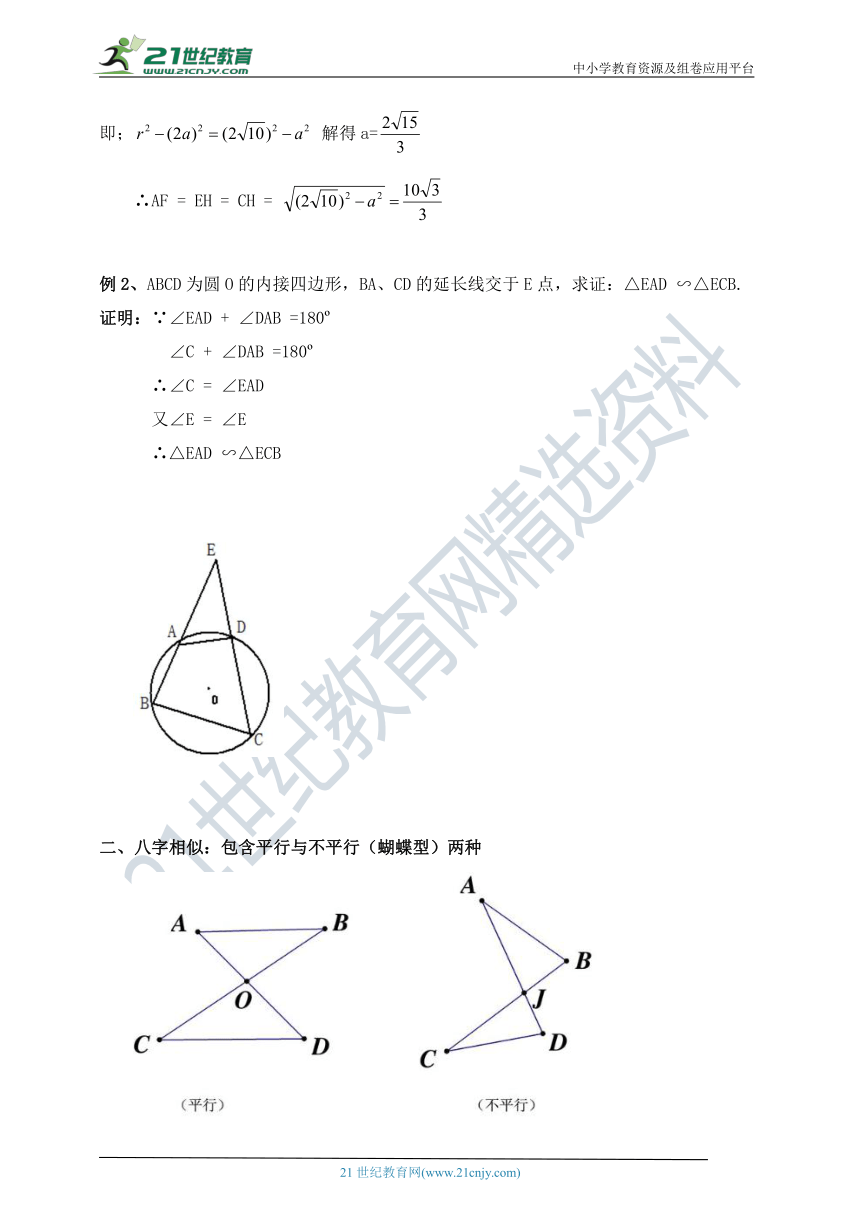
例2、ABCD为圆O的内接四边形,BA、CD的延长线交于E点,求证:△EAD ∽△ECB.
证明:∵∠EAD + ∠DAB =180
∠C + ∠DAB =180
∴∠C = ∠EAD
又∠E = ∠E
∴△EAD ∽△ECB
二、八字相似:包含平行与不平行(蝴蝶型)两种
例3、如图,AB是⊙O的直径,弦CD⊥AB与点E,点P在⊙O上,∠1=∠C,
(1)求证:△BCF∽△DPF; (2)若BC=3,sin∠P=,求⊙O的直径.
解:(1)证明:∵∠1=∠D又∵∠C=∠P ∴△BCF∽△DPF;
(2)解:连接AC∵AB为⊙O的直径,∴∠ACB=90°
又∵CD⊥AB,∴=,∴∠P=∠CAB,又∵sin∠P=,
∴sin∠CAB=,即=,又知,BC=3,∴AB=5,∴直径为5.
例4、如图,在中,是高,的外接圆直径交边于点,有下列四个结论:①;②;③;④.其中正确结论的是____________.(只填写序号)
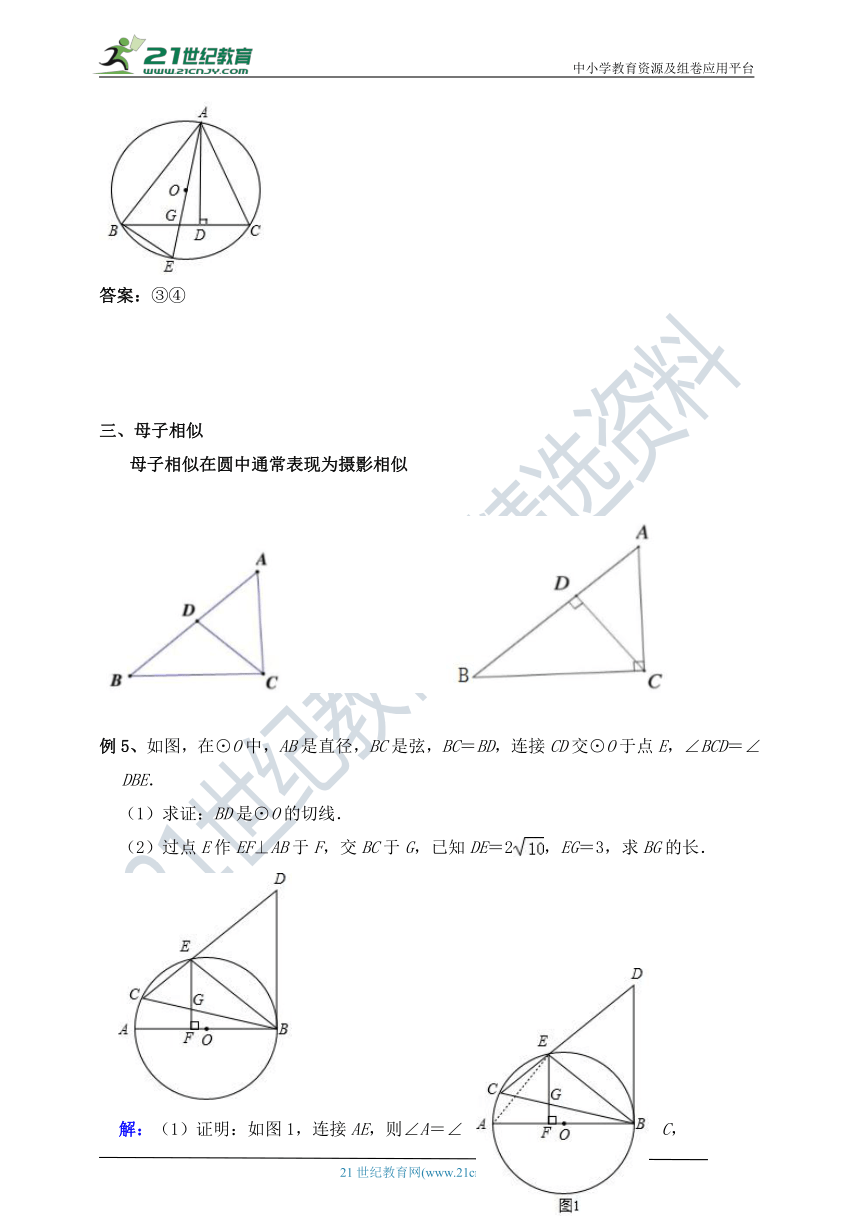
答案:③④
母子相似
母子相似在圆中通常表现为摄影相似
例5、如图,在⊙O中,AB是直径,BC是弦,BC=BD,连接CD交⊙O于点E,∠BCD=∠DBE.
(1)求证:BD是⊙O的切线.
(2)过点E作EF⊥AB于F,交BC于G,已知DE=2,EG=3,求BG的长.
解:(1)证明:如图1,连接AE,则∠A=∠C,
∵AB是直径,∴∠AEB=90°,
∴∠A+∠ABE=90°,
∵∠C=∠DBE,
∴∠ABE+∠DBE=90°,即∠ABD=90°,
∴BD是⊙O的切线
(2)解:如图2,延长EF交⊙O于H,
∵EF⊥AB,AB是直径,
∴,∴∠ECB=∠BEH,
∵∠EBC=∠GBE,∴△EBC∽△GBE,
∴,
∵BC=BD,∴∠D=∠C,
∵∠C=∠DBE,∴∠D=∠DBE,
∴BE=DE=2,
又∠AFE=∠ABD=90°,
∴BD∥EF,∴∠D=∠CEF,
∴∠C=∠CEF,∴CG=GE=3,
∴BC=BG+CG=BG+3,
∴,
∴BG=﹣8(舍)或BG=5,
即BG的长为5.
例6、如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE=∠A.
(1)求证:BC是⊙O的切线;
(2)若sinB=,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
解:(1)证明:连接OE,∵在△ABC中,∠C=90°,FG⊥BC,
∴∠BGF=∠C=90°,∴FG∥AC,∴∠OFG=∠A,
∴∠OFE=∠OFG,
∴∠OFE=∠EFG,∵OE=OF,∴∠OFE=∠OEF,∴∠OEF=∠EFG,
∴OE∥FG,∴OE⊥BC,∴BC是⊙O的切线;
(2)解:∵在Rt△OBE中,sinB=,⊙O的半径为r,∴OB=r,BE=r,
∴BF=OB+OF=r,∴FG=BF sinB=r,
∴BG==r,∴EG=BG﹣BE=r,
∴S△FGE=EG FG=r2,EG:FG=1:2,
∵BC是切线,∴∠GEH=∠EFG,∵∠EGH=∠FGE,∴△EGH∽△FGE,
∴=()2=,∴S△EHG=S△FGE=r2.
其他相似:主要是与切点有关的相似
例7、已知:如图24 19,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
(1)求证:∠BAC=∠CAD;
(2)若∠B=30°,AB=12,求的长.
解:(1)证明:如图D93,连接OC,
图D93
∵EF是过点C的⊙O的切线,
∴∠ACD = ∠ABC
又∵AD⊥EF,AB是⊙O的直径
∴∠ACB=∠ADC = 90°.
∴△ACD = △ABC ∴∠BAC=∠CAD;
(2)解:∵OB=OC,∴∠B=∠OCB=30°.
又∵∠AOC是△BOC的外角,
∴∠AOC=∠B+∠OCB=60°.
∵AB=12,∴半径OA=AB=6.
∴的长为l==2π.
例8、如图所示,在梯形ABCD中,AD∥BC,AB⊥BC,以AB为直径
的⊙O与DC相切于E.已知AB=8,边BC比AD大6.
(1)求边AD、BC的长;
(2)在直径AB上是否存在一动点P,使以A、D、P为顶点的三角形
与△BCP相似?若存在,求出AP的长;若不存在,请说明理由.
解:(1)方法1:过D作DF⊥BC于F,
在Rt△DFC中,DF=AB=8,FC=BC﹣AD=6,∴DC2=62+82=100,即DC=10.(1分)
设AD=x,则DE=AD=x,EC=BC=x+6,∴x+(x+6)=10.∴x=2.
∴AD=2,BC=2+6=8.(4分)方法2:连OD、OE、OC,
由切线长定理可知∠DOC=90°,AD=DE,CB=CE,设AD=x,则BC=x+6,
由射影定理可得:OE2=DE EC.(2分)即:x(x+6)=16,
解得x1=2,x2=﹣8,(舍去)∴AD=2,BC=2+6=8.(4分)
(2)存在符合条件的P点.
设AP=y,则BP=8﹣y,△ADP与△BCP相似,有两种情况:
①△ADP∽△BCP时,∴y=;(6分)
②△ADP∽△BPC时,∴y=4.(7分)
故存在符合条件的点P,此时AP=或4.(8分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
初中数学北师大九年级下学期第三章圆:不得不说的与圆有关的三角形相似几种模型
圆几乎是中考数学必考的压轴题型之一,因为与圆结合的图形形状有很多,比如三角形、四边形等基本图形。可见其综合性、灵活性非常高,值得我们深入细致的去学习和研究。今天我们再以三角形与圆相结合的题型,来进一步学习和探讨圆中有关三角形相似的问题。
我们知道在圆中随便相连就可以形成很多三角形,而圆是轴对称图形,有无数条对称轴,这就造成了圆的一些特殊性质,比如:
直径所对的圆周角为直角;
平分一般弦(不是直径)的直径垂直于弦;
圆的切线与过该点的半径垂直等。
因此,圆中有非常多的直角三角形,且圆中三角形的相似一般是直角三角形的相似。
这些相似包括:A字相似(平行、不平行);8字相似(平行、不平行)、摄影相似、母子相似等。
只有熟悉并熟练掌握了圆中有关三角形的相似模型,才能在考试中快速制胜!
一、A字相似:包含平行与不平行两种
A字相似在圆中通常表现为直角三角形相似的形式:
例1、如图,在RT△OAB中,∠OAB=90 ,以OA为半径的⊙O交BO于点C,交BO延长线于点D。在⊙O上取一点E,且弧AE = 弧AC,延长DE与BA交于点F
求证:△BDF是直角三角形
连接AC,AC=,OC=2BC,求AF的长。
解:(1)证明:∵弧AE = 弧AC
∴∠BDE=∠BOE=∠BOA
又∠OAB=90 ,∠B = ∠B
∴∠F = ∠OAB=90
即△BDF是直角三角形
(2)连接EC,交OA于点H
那么有OA⊥EC于点H
∴△OHC ∽ △OAB
设AH = a ,圆半径为r,那么有
∴OH =2a 3a = r
利用勾股定理得:
即; 解得a=
∴AF = EH = CH =
例2、ABCD为圆O的内接四边形,BA、CD的延长线交于E点,求证:△EAD ∽△ECB.
证明:∵∠EAD + ∠DAB =180
∠C + ∠DAB =180
∴∠C = ∠EAD
又∠E = ∠E
∴△EAD ∽△ECB
二、八字相似:包含平行与不平行(蝴蝶型)两种
例3、如图,AB是⊙O的直径,弦CD⊥AB与点E,点P在⊙O上,∠1=∠C,
(1)求证:△BCF∽△DPF; (2)若BC=3,sin∠P=,求⊙O的直径.
解:(1)证明:∵∠1=∠D又∵∠C=∠P ∴△BCF∽△DPF;
(2)解:连接AC∵AB为⊙O的直径,∴∠ACB=90°
又∵CD⊥AB,∴=,∴∠P=∠CAB,又∵sin∠P=,
∴sin∠CAB=,即=,又知,BC=3,∴AB=5,∴直径为5.
例4、如图,在中,是高,的外接圆直径交边于点,有下列四个结论:①;②;③;④.其中正确结论的是____________.(只填写序号)
答案:③④
母子相似
母子相似在圆中通常表现为摄影相似
例5、如图,在⊙O中,AB是直径,BC是弦,BC=BD,连接CD交⊙O于点E,∠BCD=∠DBE.
(1)求证:BD是⊙O的切线.
(2)过点E作EF⊥AB于F,交BC于G,已知DE=2,EG=3,求BG的长.
解:(1)证明:如图1,连接AE,则∠A=∠C,
∵AB是直径,∴∠AEB=90°,
∴∠A+∠ABE=90°,
∵∠C=∠DBE,
∴∠ABE+∠DBE=90°,即∠ABD=90°,
∴BD是⊙O的切线
(2)解:如图2,延长EF交⊙O于H,
∵EF⊥AB,AB是直径,
∴,∴∠ECB=∠BEH,
∵∠EBC=∠GBE,∴△EBC∽△GBE,
∴,
∵BC=BD,∴∠D=∠C,
∵∠C=∠DBE,∴∠D=∠DBE,
∴BE=DE=2,
又∠AFE=∠ABD=90°,
∴BD∥EF,∴∠D=∠CEF,
∴∠C=∠CEF,∴CG=GE=3,
∴BC=BG+CG=BG+3,
∴,
∴BG=﹣8(舍)或BG=5,
即BG的长为5.
例6、如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE=∠A.
(1)求证:BC是⊙O的切线;
(2)若sinB=,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
解:(1)证明:连接OE,∵在△ABC中,∠C=90°,FG⊥BC,
∴∠BGF=∠C=90°,∴FG∥AC,∴∠OFG=∠A,
∴∠OFE=∠OFG,
∴∠OFE=∠EFG,∵OE=OF,∴∠OFE=∠OEF,∴∠OEF=∠EFG,
∴OE∥FG,∴OE⊥BC,∴BC是⊙O的切线;
(2)解:∵在Rt△OBE中,sinB=,⊙O的半径为r,∴OB=r,BE=r,
∴BF=OB+OF=r,∴FG=BF sinB=r,
∴BG==r,∴EG=BG﹣BE=r,
∴S△FGE=EG FG=r2,EG:FG=1:2,
∵BC是切线,∴∠GEH=∠EFG,∵∠EGH=∠FGE,∴△EGH∽△FGE,
∴=()2=,∴S△EHG=S△FGE=r2.
其他相似:主要是与切点有关的相似
例7、已知:如图24 19,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
(1)求证:∠BAC=∠CAD;
(2)若∠B=30°,AB=12,求的长.
解:(1)证明:如图D93,连接OC,
图D93
∵EF是过点C的⊙O的切线,
∴∠ACD = ∠ABC
又∵AD⊥EF,AB是⊙O的直径
∴∠ACB=∠ADC = 90°.
∴△ACD = △ABC ∴∠BAC=∠CAD;
(2)解:∵OB=OC,∴∠B=∠OCB=30°.
又∵∠AOC是△BOC的外角,
∴∠AOC=∠B+∠OCB=60°.
∵AB=12,∴半径OA=AB=6.
∴的长为l==2π.
例8、如图所示,在梯形ABCD中,AD∥BC,AB⊥BC,以AB为直径
的⊙O与DC相切于E.已知AB=8,边BC比AD大6.
(1)求边AD、BC的长;
(2)在直径AB上是否存在一动点P,使以A、D、P为顶点的三角形
与△BCP相似?若存在,求出AP的长;若不存在,请说明理由.
解:(1)方法1:过D作DF⊥BC于F,
在Rt△DFC中,DF=AB=8,FC=BC﹣AD=6,∴DC2=62+82=100,即DC=10.(1分)
设AD=x,则DE=AD=x,EC=BC=x+6,∴x+(x+6)=10.∴x=2.
∴AD=2,BC=2+6=8.(4分)方法2:连OD、OE、OC,
由切线长定理可知∠DOC=90°,AD=DE,CB=CE,设AD=x,则BC=x+6,
由射影定理可得:OE2=DE EC.(2分)即:x(x+6)=16,
解得x1=2,x2=﹣8,(舍去)∴AD=2,BC=2+6=8.(4分)
(2)存在符合条件的P点.
设AP=y,则BP=8﹣y,△ADP与△BCP相似,有两种情况:
①△ADP∽△BCP时,∴y=;(6分)
②△ADP∽△BPC时,∴y=4.(7分)
故存在符合条件的点P,此时AP=或4.(8分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
