2021-2022学年北师大版数学九年级下册第二章二次函数复习课件(共25张PPT)
文档属性
| 名称 | 2021-2022学年北师大版数学九年级下册第二章二次函数复习课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 426.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 15:32:03 | ||
图片预览





文档简介
(共25张PPT)
2.6. 回顾与思考
第二章 二次函数
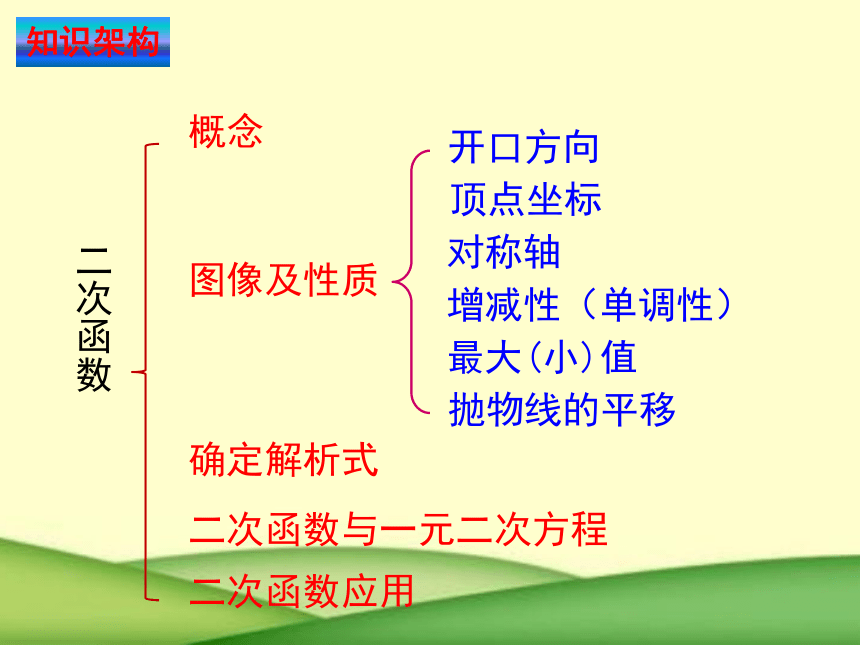
知识架构
开口方向
抛物线的平移
确定解析式
二次函数
概念
图像及性质
二次函数与一元二次方程
二次函数应用
顶点坐标
对称轴
增减性(单调性)
最大(小)值
知识回顾
一般地,若两个变量x、y之间的对应关系可以表示成
则称y是x的二次函数。
的形式,
一.二次函数的概念
y=ax2+bx+c
(a、b 、c是常数,a≠0)
y=ax2
(a≠0 、b=0 、c=0)
y=ax2 +c
(a≠0 、b=0 、c≠0)
y=ax2 +bx
(a≠0 、b≠0 、c=0)
练一练
1.二次函数y=3x-x 中a =___, b=___, c=___
-1
3
0
≠0
=0
≠0
3.已知函数y= a x + bx+c(其中a,b,c是常数)
(1)当a____时是二次函数
(2)当a____, b____时是一次函数
2.函数y=(m-1)x +3x+1,当m=___时,它是二次函数
m +1
-1
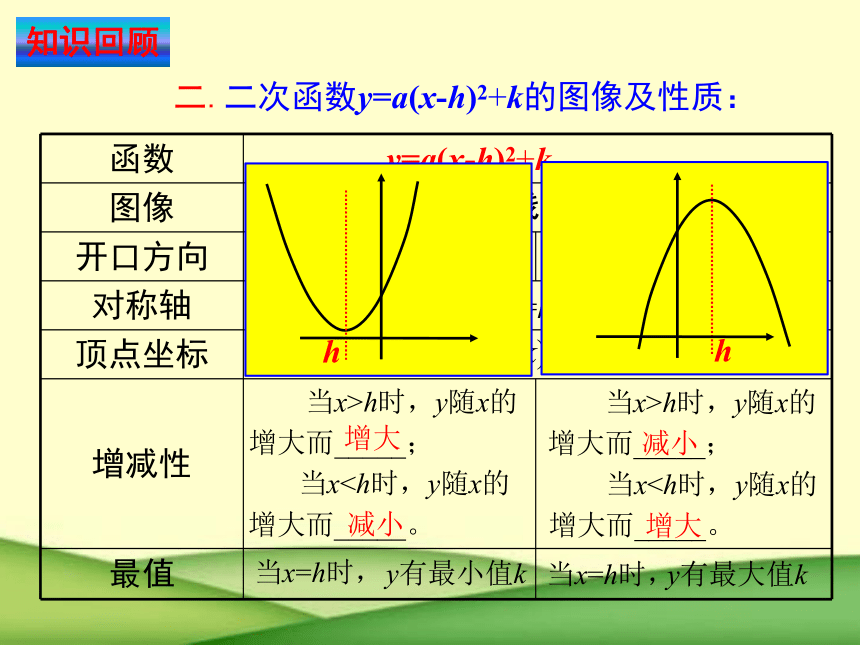
二.二次函数y=a(x-h)2+k的图像及性质:
函数
图像
开口方向
对称轴
顶点坐标
增减性
最值
直线x=h
a>0,
a<0,
(h,k)
当x>h时,y随x的
增大而_____;
当x=h时,
当x=h时,
当x>h时,y随x的
增大而_____;
抛物线
向下
向上
当x增大而_____。
增大
减小
当x增大而_____。
增大
减小
y有最小值k
y有最大值k
y=a(x-h)2+k
h
h
知识回顾
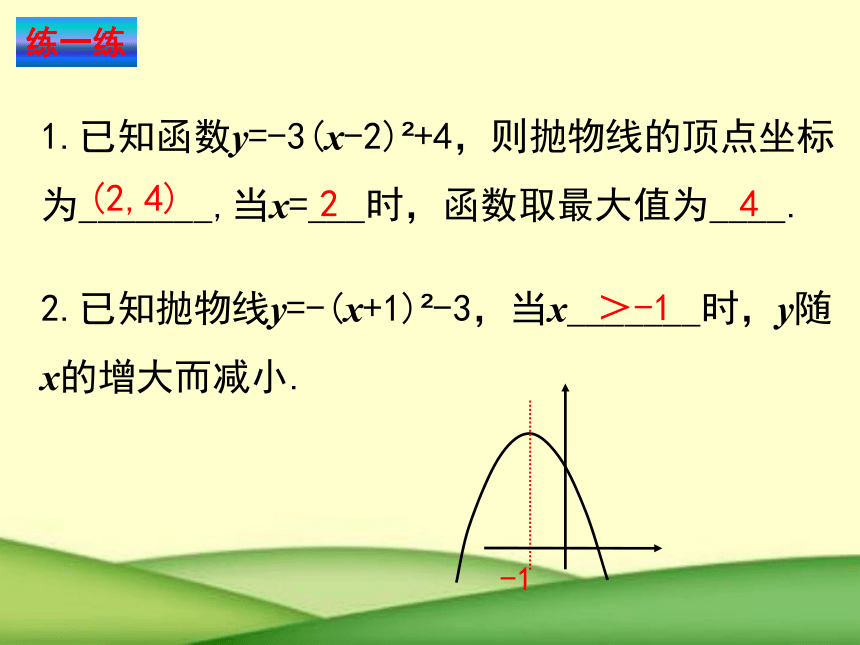
练一练
1.已知函数y=-3(x-2) +4,则抛物线的顶点坐标为_______,当x=___时,函数取最大值为____.
2
4
(2,4)
2.已知抛物线y=-(x+1) -3,当x_______时,y随x的增大而减小.
>-1
-1
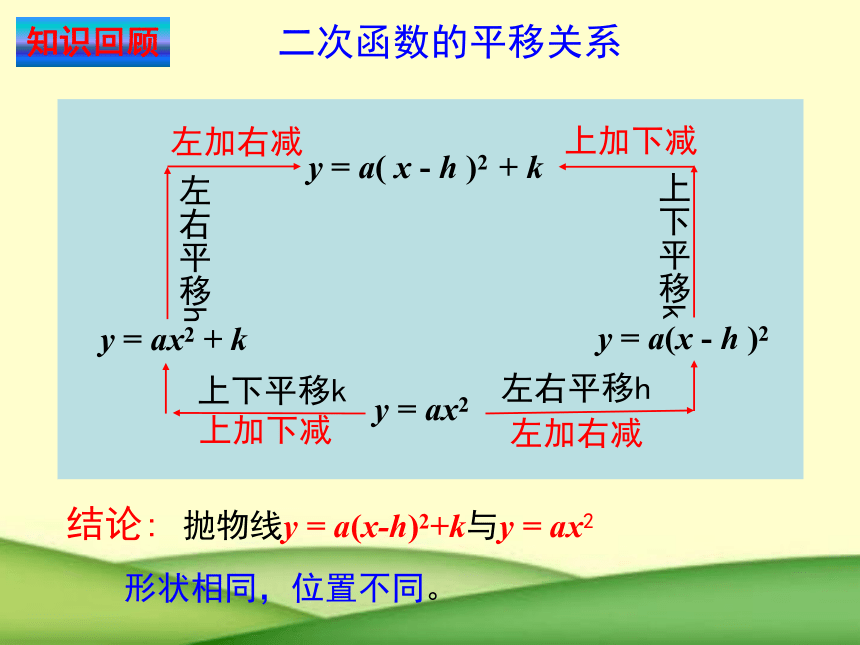
y = ax2
y = ax2 + k
y = a(x - h )2
y = a( x - h )2 + k
上下平移k
左右平移h
上下平移k
左右平移h
结论:
二次函数的平移关系
左加右减
上加下减
形状相同,位置不同。
抛物线y = a(x-h)2+k与y = ax2
左加右减
上加下减
知识回顾
1.把二次函数y=(x-2)2的图像,沿y轴向上
3.把二次函数___________的图像,先向右平移1个
平移3个单位,得到_____________的图像;
单位,再向下平移2个单位,得到y= x2+1的图像.
y=(x-2)2+3
y=(x+1)2+3
练一练
2.把二次函数y=(x-1)2的图像,沿x轴向左平移
3个单位,得到_____________的图像;
y=(x+2)2
y = a( x - h )2 + k
a(x+ )
b
2a
+
4ac-b
4a
y=ax +bx+c
二次函数顶点公式
因此,抛物线y=ax +bx+c的
对称轴是:直线
顶点坐标是:
x=-
b
2a
y=
b
2a
-
(
,
4ac-b
4a
)
知识回顾
当a>0时,开口向___,
在对称轴右侧,y的值随x值的增大而_____.
在对称轴左侧,y的值随x值的增大而_____;
时,
x=-
b
2a
函数y有最___值
4ac-b
4a
上
减小
增大
小
知识回顾
当a < 0时,开口向___,
在对称轴右侧,y的值随x值的增大而_____.
在对称轴左侧,y的值随x值的增大而_____;
时,
x=-
b
2a
函数y有最___值
4ac-b
4a
下
减小
增大
大
知识回顾
练一练
如图所示的抛物线:
当x=_______时,y=0;
当x<-2或x>0时, y_____0;
当x在____________ 范围内时,y>0;
当x=_____时,y有最大值_____.
0或-2
<
-2<x<0
-1
3
-1
-2
y
x
O
3
三.确定二次函数表达式的方法:
(1)对于一般式y=ax2+bx+c,
再加_____条件就可以确定表达式;
已知一项的系数,
两个
(2)对于顶点坐标式y=a(x-h)2+k 。
再加_____条件就可以确定表达式。
已知顶点坐标,
一个
(3)对于一般式y=ax2+bx+c,
需要_____条件就可以确定表达式
三个
知识回顾
练一练
1.设抛物线y=x +8x-k的顶点在x轴上,则k的值为( )
A.-16 B.16 C.-8 D.8
A
3.已知二次函数y=ax +x+a(a-2)的图象经过原点,
则a的值为( )
A.0或2 B.0 C.2 D.无法确定
2.将抛物线y=3x +1绕原点O旋转180°则旋转后的
抛物线的解析式为( )
A. y=- x +1 B. y=- x -1
C. y=-3x -1 D. y=-3x +1
1
3
1
3
C
C
四.二次函数y=ax2+bx+c与一元二次方程的关系:
判别式 Δ=b2-4ac
Δ>0
有两个交点
有两个不相等的实根
Δ=0
有一个交点
有两个相等的实根
Δ<0
没有交点
没有实根
与x轴的交点
根的情况
二次函数
y=ax2+bx+c(a≠0)
一元二次方程
ax2+bx+c=0(a≠0)
二次函数y=ax +bx+c的图象与x轴交点的横坐标就是一元二次方程ax +bx+c=0的根
知识回顾
练一练
1抛物线y=3x -x+4与坐标轴的交点个数是( )
A.3 B.2 C.1 D.0
D
2.已知抛物线y=x -x-1与x轴的一个交点坐标为(m,0)则代数式m -m+5=
将(m,0)代入
y=x -x-1
m -m-1=0
m -m+5=
m -m-1+6
6
练一练
3.若关于x的一元二次方程x -x-n=0没有实数根则
抛物线y=x -x-n的顶点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
∵方程x -x-n=0没有实数根
∴Δ=1+4n
<0
y=x -x-n
=(x - )
1
2
-n
1
4
-
=(x - )
1
2
1+4n
4
-
∴顶点为( , )
1
2
1+4n
4
-
A
知识延展
二次函数
y=ax2+bx+c的图象
与a,b,c的关系
新知探究
y=ax +bx+c
a>0
a<0
a
a的符号,决定图象的
开口方向
a
大小,决定图象的
开口大小
新知探究
y=ax +bx+c
b=0
a,b同号
a,b异号
对称轴是y轴
对称轴在y轴左侧
对称轴在y轴右侧
a,b决定对称轴位置
对称轴是直线x=-
b
2a
(ab>0)
(ab<0)
新知探究
y=ax +bx+c
c=0
c>0
c<0
坐标原点
y轴于正半轴
交y轴于负半轴
图象过
图象交
图象交
c是图象与y轴交点的纵坐标
(0,0)
(0,c)
(0,c)
新知探究
b -4ac=0
y=ax +bx+c
b -4ac>0
b -4ac<0
b -4ac
决定了图象与x轴的交点
与x轴有
与x轴有
与x轴
唯一交点
两个交点
没有交点
新知探究
y=ax +bx+c
求:a+b+c 的值
将x =1代入函数关系式
y=a+b+c
求:a-b+c 的值
将x =-1代入函数关系式
y=a-b+c
归纳
字母
字母的符号
图像的特征
a>0
b=0
开口向上
开口向下
二次函数y=ax2+bx+c的图象与a,b,c的关系
a<0
对称轴为y轴
b-4ac
a
b
c
ab>0
ab<0
对称轴在y轴左侧
对称轴在y轴右侧
c>0
c=0
c<0
b-4ac>0
b-4ac=0
b-4ac<0
经过原点
与y轴正半轴相交
与y轴负半轴相交
与x轴有唯一交点(顶点)
与x轴有两个交点
与x轴没有交点
(a,b同号)
(a,b异号)
练一练
.二次函数y=ax +bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
下列结论:
(1)ac<0;
(2)当x>1时,y的值随x值的增大而减小;
(3)3是方程ax +(b-1)x+c=0的一个根;
(4)当-1<x<3时、 ax +(b-1)x+c>0其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
x -1 0 1 3
y -1 3 5 3
x
O
-3 -2 -1 1 2 3 4
y
6
5
4
3
2
1
-1
x
O
-3 -2 -1 1 2 3 4
y
6
5
4
3
2
1
-1
2.6. 回顾与思考
第二章 二次函数
知识架构
开口方向
抛物线的平移
确定解析式
二次函数
概念
图像及性质
二次函数与一元二次方程
二次函数应用
顶点坐标
对称轴
增减性(单调性)
最大(小)值
知识回顾
一般地,若两个变量x、y之间的对应关系可以表示成
则称y是x的二次函数。
的形式,
一.二次函数的概念
y=ax2+bx+c
(a、b 、c是常数,a≠0)
y=ax2
(a≠0 、b=0 、c=0)
y=ax2 +c
(a≠0 、b=0 、c≠0)
y=ax2 +bx
(a≠0 、b≠0 、c=0)
练一练
1.二次函数y=3x-x 中a =___, b=___, c=___
-1
3
0
≠0
=0
≠0
3.已知函数y= a x + bx+c(其中a,b,c是常数)
(1)当a____时是二次函数
(2)当a____, b____时是一次函数
2.函数y=(m-1)x +3x+1,当m=___时,它是二次函数
m +1
-1
二.二次函数y=a(x-h)2+k的图像及性质:
函数
图像
开口方向
对称轴
顶点坐标
增减性
最值
直线x=h
a>0,
a<0,
(h,k)
当x>h时,y随x的
增大而_____;
当x=h时,
当x=h时,
当x>h时,y随x的
增大而_____;
抛物线
向下
向上
当x
增大
减小
当x
增大
减小
y有最小值k
y有最大值k
y=a(x-h)2+k
h
h
知识回顾
练一练
1.已知函数y=-3(x-2) +4,则抛物线的顶点坐标为_______,当x=___时,函数取最大值为____.
2
4
(2,4)
2.已知抛物线y=-(x+1) -3,当x_______时,y随x的增大而减小.
>-1
-1
y = ax2
y = ax2 + k
y = a(x - h )2
y = a( x - h )2 + k
上下平移k
左右平移h
上下平移k
左右平移h
结论:
二次函数的平移关系
左加右减
上加下减
形状相同,位置不同。
抛物线y = a(x-h)2+k与y = ax2
左加右减
上加下减
知识回顾
1.把二次函数y=(x-2)2的图像,沿y轴向上
3.把二次函数___________的图像,先向右平移1个
平移3个单位,得到_____________的图像;
单位,再向下平移2个单位,得到y= x2+1的图像.
y=(x-2)2+3
y=(x+1)2+3
练一练
2.把二次函数y=(x-1)2的图像,沿x轴向左平移
3个单位,得到_____________的图像;
y=(x+2)2
y = a( x - h )2 + k
a(x+ )
b
2a
+
4ac-b
4a
y=ax +bx+c
二次函数顶点公式
因此,抛物线y=ax +bx+c的
对称轴是:直线
顶点坐标是:
x=-
b
2a
y=
b
2a
-
(
,
4ac-b
4a
)
知识回顾
当a>0时,开口向___,
在对称轴右侧,y的值随x值的增大而_____.
在对称轴左侧,y的值随x值的增大而_____;
时,
x=-
b
2a
函数y有最___值
4ac-b
4a
上
减小
增大
小
知识回顾
当a < 0时,开口向___,
在对称轴右侧,y的值随x值的增大而_____.
在对称轴左侧,y的值随x值的增大而_____;
时,
x=-
b
2a
函数y有最___值
4ac-b
4a
下
减小
增大
大
知识回顾
练一练
如图所示的抛物线:
当x=_______时,y=0;
当x<-2或x>0时, y_____0;
当x在____________ 范围内时,y>0;
当x=_____时,y有最大值_____.
0或-2
<
-2<x<0
-1
3
-1
-2
y
x
O
3
三.确定二次函数表达式的方法:
(1)对于一般式y=ax2+bx+c,
再加_____条件就可以确定表达式;
已知一项的系数,
两个
(2)对于顶点坐标式y=a(x-h)2+k 。
再加_____条件就可以确定表达式。
已知顶点坐标,
一个
(3)对于一般式y=ax2+bx+c,
需要_____条件就可以确定表达式
三个
知识回顾
练一练
1.设抛物线y=x +8x-k的顶点在x轴上,则k的值为( )
A.-16 B.16 C.-8 D.8
A
3.已知二次函数y=ax +x+a(a-2)的图象经过原点,
则a的值为( )
A.0或2 B.0 C.2 D.无法确定
2.将抛物线y=3x +1绕原点O旋转180°则旋转后的
抛物线的解析式为( )
A. y=- x +1 B. y=- x -1
C. y=-3x -1 D. y=-3x +1
1
3
1
3
C
C
四.二次函数y=ax2+bx+c与一元二次方程的关系:
判别式 Δ=b2-4ac
Δ>0
有两个交点
有两个不相等的实根
Δ=0
有一个交点
有两个相等的实根
Δ<0
没有交点
没有实根
与x轴的交点
根的情况
二次函数
y=ax2+bx+c(a≠0)
一元二次方程
ax2+bx+c=0(a≠0)
二次函数y=ax +bx+c的图象与x轴交点的横坐标就是一元二次方程ax +bx+c=0的根
知识回顾
练一练
1抛物线y=3x -x+4与坐标轴的交点个数是( )
A.3 B.2 C.1 D.0
D
2.已知抛物线y=x -x-1与x轴的一个交点坐标为(m,0)则代数式m -m+5=
将(m,0)代入
y=x -x-1
m -m-1=0
m -m+5=
m -m-1+6
6
练一练
3.若关于x的一元二次方程x -x-n=0没有实数根则
抛物线y=x -x-n的顶点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
∵方程x -x-n=0没有实数根
∴Δ=1+4n
<0
y=x -x-n
=(x - )
1
2
-n
1
4
-
=(x - )
1
2
1+4n
4
-
∴顶点为( , )
1
2
1+4n
4
-
A
知识延展
二次函数
y=ax2+bx+c的图象
与a,b,c的关系
新知探究
y=ax +bx+c
a>0
a<0
a
a的符号,决定图象的
开口方向
a
大小,决定图象的
开口大小
新知探究
y=ax +bx+c
b=0
a,b同号
a,b异号
对称轴是y轴
对称轴在y轴左侧
对称轴在y轴右侧
a,b决定对称轴位置
对称轴是直线x=-
b
2a
(ab>0)
(ab<0)
新知探究
y=ax +bx+c
c=0
c>0
c<0
坐标原点
y轴于正半轴
交y轴于负半轴
图象过
图象交
图象交
c是图象与y轴交点的纵坐标
(0,0)
(0,c)
(0,c)
新知探究
b -4ac=0
y=ax +bx+c
b -4ac>0
b -4ac<0
b -4ac
决定了图象与x轴的交点
与x轴有
与x轴有
与x轴
唯一交点
两个交点
没有交点
新知探究
y=ax +bx+c
求:a+b+c 的值
将x =1代入函数关系式
y=a+b+c
求:a-b+c 的值
将x =-1代入函数关系式
y=a-b+c
归纳
字母
字母的符号
图像的特征
a>0
b=0
开口向上
开口向下
二次函数y=ax2+bx+c的图象与a,b,c的关系
a<0
对称轴为y轴
b-4ac
a
b
c
ab>0
ab<0
对称轴在y轴左侧
对称轴在y轴右侧
c>0
c=0
c<0
b-4ac>0
b-4ac=0
b-4ac<0
经过原点
与y轴正半轴相交
与y轴负半轴相交
与x轴有唯一交点(顶点)
与x轴有两个交点
与x轴没有交点
(a,b同号)
(a,b异号)
练一练
.二次函数y=ax +bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
下列结论:
(1)ac<0;
(2)当x>1时,y的值随x值的增大而减小;
(3)3是方程ax +(b-1)x+c=0的一个根;
(4)当-1<x<3时、 ax +(b-1)x+c>0其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
x -1 0 1 3
y -1 3 5 3
x
O
-3 -2 -1 1 2 3 4
y
6
5
4
3
2
1
-1
x
O
-3 -2 -1 1 2 3 4
y
6
5
4
3
2
1
-1
