北师大版 九年级数学下册 二次函数与圆 课件(共22张ppt)
文档属性
| 名称 | 北师大版 九年级数学下册 二次函数与圆 课件(共22张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-23 19:22:50 | ||
图片预览







文档简介
(共22张PPT)
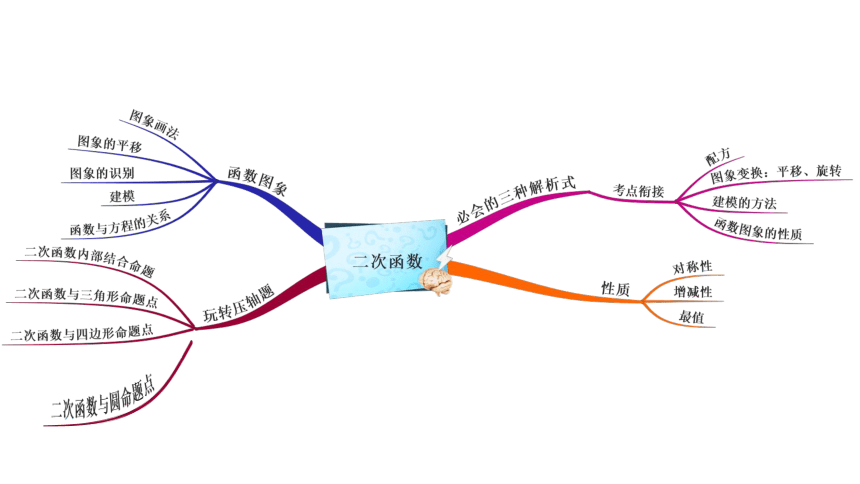
二次函数与圆
学习内容
历年中考考点分析
1
知识梳理
2
典例精讲
3
总结
4
2016年 22题 考察圆的有关知识(利用圆翻折、求线段的长、证明切线、动点相似求线段积)
23题 二次函数综合(求表达式、利用角平分线求坐标、求面积最值问题)
2017年 22题 考察圆的有关知识(勾股定理求半径、角的转化、三角函数值、利用三角形相似求线段积)
23题 二次函数综合(求表达式、利用面积求坐标、利用旋转求线段长度)
2018年 22题 考察圆的有关知识(利用角动点构造等腰三角形、求线段长、根据全等求线段的和)
23题 二次函数综合(求表达式、利用相似三角形求面积、翻折、根据相似求点的坐标)
2019年 22题 二次函数综合(求表达式、对称轴、利用四边形周长求最值、根据面积比求坐标)
23题 考察圆的有关知识(证明切线、相似三角形、对称性、根据角求点坐标,求线段比值最值)
一、深圳历年中考二次函数与圆的考点分析
二、二次函数与圆
知识梳理
三、典例精讲
x
y
(1)点B,C的坐标分别为B(________),C(___________);
(2)是否存在点P,使得△PBC为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)连结PB,若E为PB的中点,连结OE,则OE的最大值为?
P
【分析】 (1)令y=0,可求得点B的坐标,令x=0,求出点C的坐标
3,0
(1)点B,C的坐标分别为B(________),C(___________);
0,-4
3、
【分析】 :(2)分类讨论,若∠BPC=90°,若∠BCP=90°时,若∠PBC=90°时分别求出点P的坐标
3、
(2)是否存在点P,使得△PBC为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
综上所述,符合条件的P点共有4个,分别是:
P
(3)如图,连接BC,取BC中点T,连结OT,TE,CP,
∵E为BP的中点,
3、
(3)连结PB,若E为PB的中点,连结OE,则OE的最大值为?
P
E
P
E
(3)法2:连接AP,∵O是AB的中点,E是BP中点,则OE是△ABP的中位线,当AP最大时则OE也最大
【点评】此题主要考查了二次函数与圆的相关知识,涉及到的考点有二次函数的性质、勾股定理及其二次方程、中位线等知识,注意第二问不要漏解.
y
x
C
B
A
O
y
x
C
B
A
O
y
x
C
B
A
O
E
F
图2
M
y
x
C
B
A
O
E
F
图2
M
∴
y
x
C
B
A
O
E
F
图2
y
x
C
B
A
O
【点评】本题考查了函数图象的性质、相似三角形性质、一元二次方程及圆的基本知识.题目特殊,貌似思路不难,但若思路不对,计算异常复杂,题目所折射出来的思想,考生应好好理解掌握.
y
x
C
B
A
O
E
F
图2
(3)利用直角三角形两直角边斜率相乘等于-1来求
分类讨论思想
总结
谢谢同学们!
二次函数与圆
学习内容
历年中考考点分析
1
知识梳理
2
典例精讲
3
总结
4
2016年 22题 考察圆的有关知识(利用圆翻折、求线段的长、证明切线、动点相似求线段积)
23题 二次函数综合(求表达式、利用角平分线求坐标、求面积最值问题)
2017年 22题 考察圆的有关知识(勾股定理求半径、角的转化、三角函数值、利用三角形相似求线段积)
23题 二次函数综合(求表达式、利用面积求坐标、利用旋转求线段长度)
2018年 22题 考察圆的有关知识(利用角动点构造等腰三角形、求线段长、根据全等求线段的和)
23题 二次函数综合(求表达式、利用相似三角形求面积、翻折、根据相似求点的坐标)
2019年 22题 二次函数综合(求表达式、对称轴、利用四边形周长求最值、根据面积比求坐标)
23题 考察圆的有关知识(证明切线、相似三角形、对称性、根据角求点坐标,求线段比值最值)
一、深圳历年中考二次函数与圆的考点分析
二、二次函数与圆
知识梳理
三、典例精讲
x
y
(1)点B,C的坐标分别为B(________),C(___________);
(2)是否存在点P,使得△PBC为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)连结PB,若E为PB的中点,连结OE,则OE的最大值为?
P
【分析】 (1)令y=0,可求得点B的坐标,令x=0,求出点C的坐标
3,0
(1)点B,C的坐标分别为B(________),C(___________);
0,-4
3、
【分析】 :(2)分类讨论,若∠BPC=90°,若∠BCP=90°时,若∠PBC=90°时分别求出点P的坐标
3、
(2)是否存在点P,使得△PBC为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
综上所述,符合条件的P点共有4个,分别是:
P
(3)如图,连接BC,取BC中点T,连结OT,TE,CP,
∵E为BP的中点,
3、
(3)连结PB,若E为PB的中点,连结OE,则OE的最大值为?
P
E
P
E
(3)法2:连接AP,∵O是AB的中点,E是BP中点,则OE是△ABP的中位线,当AP最大时则OE也最大
【点评】此题主要考查了二次函数与圆的相关知识,涉及到的考点有二次函数的性质、勾股定理及其二次方程、中位线等知识,注意第二问不要漏解.
y
x
C
B
A
O
y
x
C
B
A
O
y
x
C
B
A
O
E
F
图2
M
y
x
C
B
A
O
E
F
图2
M
∴
y
x
C
B
A
O
E
F
图2
y
x
C
B
A
O
【点评】本题考查了函数图象的性质、相似三角形性质、一元二次方程及圆的基本知识.题目特殊,貌似思路不难,但若思路不对,计算异常复杂,题目所折射出来的思想,考生应好好理解掌握.
y
x
C
B
A
O
E
F
图2
(3)利用直角三角形两直角边斜率相乘等于-1来求
分类讨论思想
总结
谢谢同学们!
