初中数学北师大版九年级下册2022中考专题 动态几何 (共15张ppt)
文档属性
| 名称 | 初中数学北师大版九年级下册2022中考专题 动态几何 (共15张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 9.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-25 07:34:05 | ||
图片预览

文档简介
(共15张PPT)
中考专题复习
-----动态几何中隐形圆问题
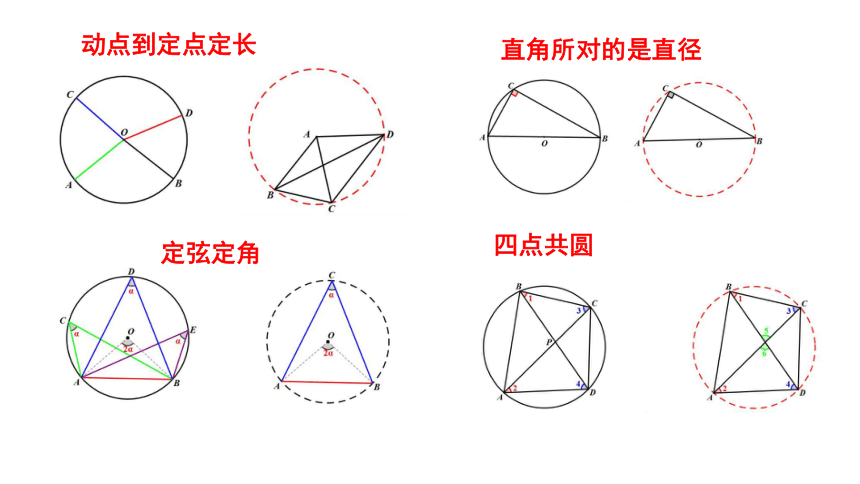
动点到定点定长
定弦定角
直角所对的是直径
四点共圆
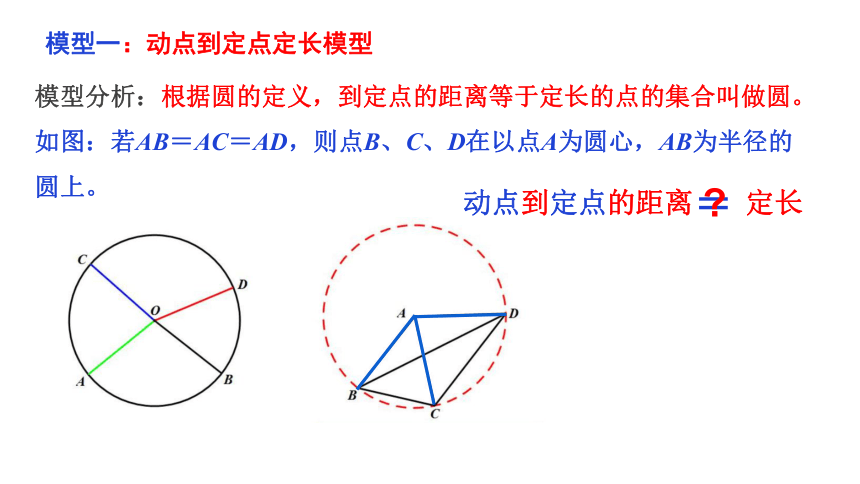
模型分析:根据圆的定义,到定点的距离等于定长的点的集合叫做圆。
如图:若AB=AC=AD,则点B、C、D在以点A为圆心,AB为半径的圆上。
模型一:动点到定点定长模型
=
动点到定点的距离
定长
O
P
G
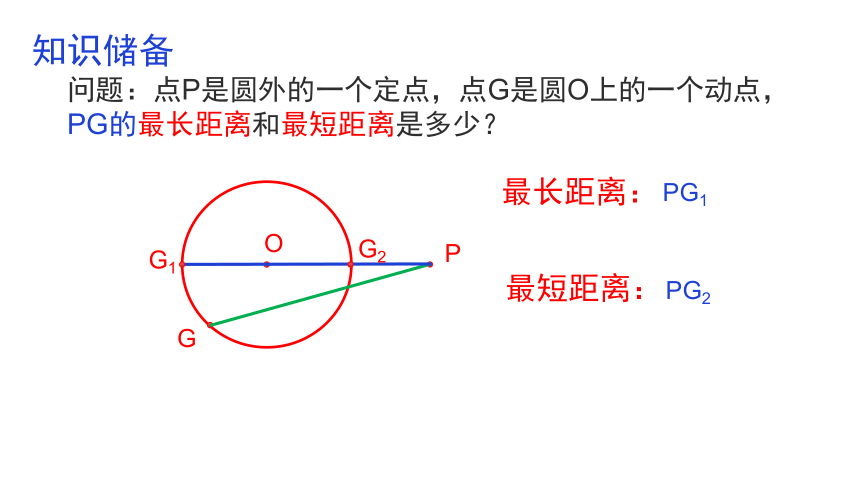
问题:点P是圆外的一个定点,点G是圆O上的一个动点, PG的最长距离和最短距离是多少?
知识储备
G1
G2
最长距离:
最短距离:
PG1
PG2
米
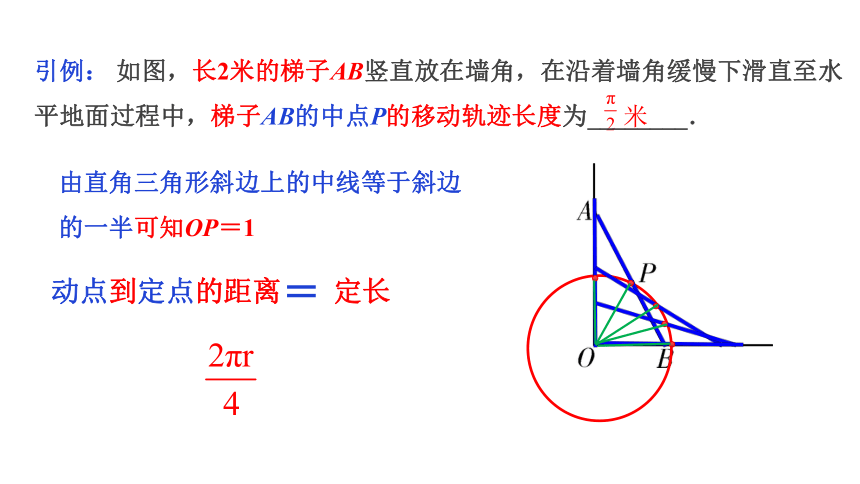
引例: 如图,长2米的梯子AB竖直放在墙角,在沿着墙角缓慢下滑直至水平地面过程中,梯子AB的中点P的移动轨迹长度为________.
由直角三角形斜边上的中线等于斜边的一半可知OP=1
=
动点到定点的距离
定长
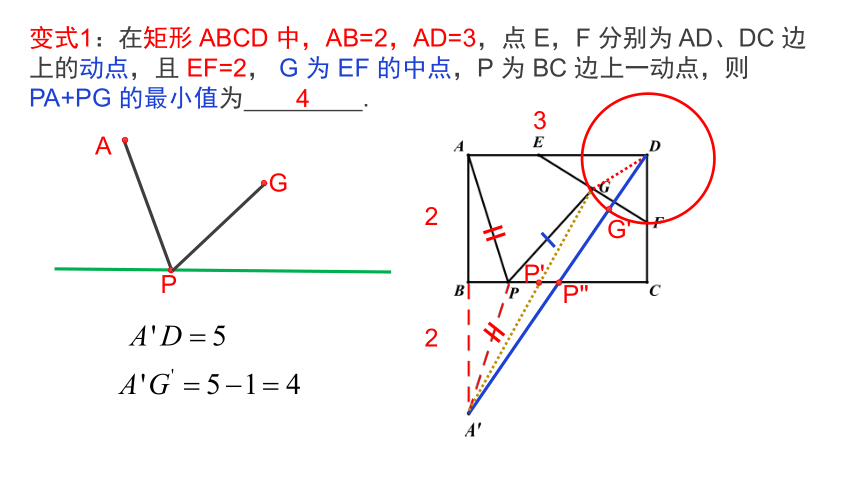
变式1:在矩形 ABCD 中,AB=2,AD=3,点 E,F 分别为 AD、DC 边上的动点,且 EF=2, G 为 EF 的中点,P 为 BC 边上一动点,则 PA+PG 的最小值为 .
P''
G'
P'
2
2
3
P
A
G
4
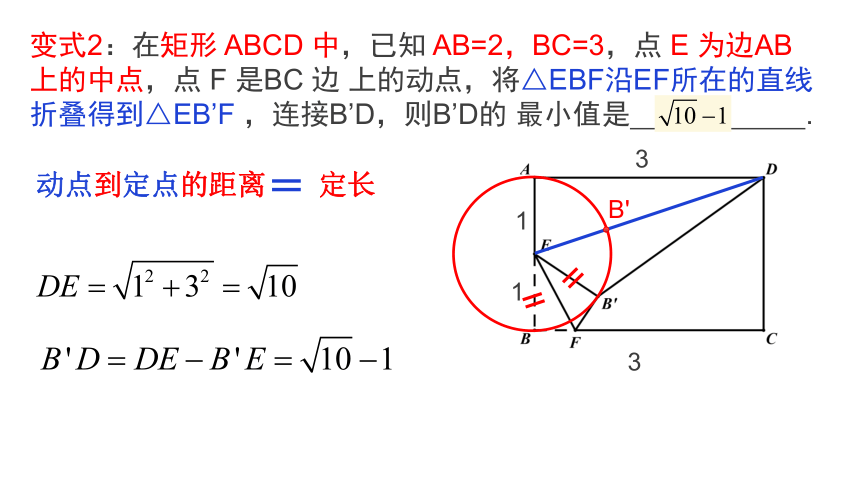
变式2:在矩形 ABCD 中,已知 AB=2,BC=3,点 E 为边AB上的中点,点 F 是BC 边 上的动点,将△EBF沿EF所在的直线折叠得到△EB’F ,连接B’D,则B’D的 最小值是 .
B'
1
1
3
3
=
动点到定点的距离
定长
变式3:在平行四边形ABCD 中,∠BCD=30°,BC=4,CD= ,M 是 AD 边的中点,N 是 AB 边上一动点,将△AMN 沿 MN 所在直线翻折得到△A'MN,连接 MC,
则 A'C 长度的最小值是 。
2
2
A''
H
30°
1
=
动点到定点的距离
定长
5
变式4:在 Rt△ABC 中,∠C=90°,AC=6,BC=8,点 F 在边 AC 上,并且 CF=2,点 E 为边 BC 上的动点,将△CEF 沿直线 EF 翻折,点 C 落在点 P 处。
(1)点 P 到边 AB 距离的最小值是 。
变式: △ABP的面积的最小值是 。
H
P'
2
4
10
=
动点到定点的距离
定长
8
6
变式5:如图,等边△ABC中,AB=6,点D在BC上,BD=4,点E为边AC上一动点(不与点C重合),△CDE关于DE的轴对称图形为△FDE.(1)求△ABF的面积的最小值为 。
F'
H
6
例1:如图,等边△ABC中,AB=6,点D在BC上,BD=4,点E为边AC上一动点
(不与点C重合),△CDE关于DE的轴对称图形为△FDE.
设△ACD的面积为S1,△ABF的面积为S2,记S=S1-S2,
S是否存在最大值?若存在,求出S的最大值;
若不存在,请说明理由;
F'
H
4
2
2
6
2
G
6
例1:如图,等边△ABC中,AB=6,点D在BC上,BD=4,点E为边AC上一动点
(不与点C重合),△CDE关于DE的轴对称图形为△FDE.
设△ACD的面积为S1,△ABF的面积为S2,记S=S1-S2,
S是否存在最大值?若存在,求出S的最大值;
若不存在,请说明理由;
小结
模型三
模型二
模型一:动点到定点定长模型
课后思考题
同学们再见!
中考专题复习
-----动态几何中隐形圆问题
动点到定点定长
定弦定角
直角所对的是直径
四点共圆
模型分析:根据圆的定义,到定点的距离等于定长的点的集合叫做圆。
如图:若AB=AC=AD,则点B、C、D在以点A为圆心,AB为半径的圆上。
模型一:动点到定点定长模型
=
动点到定点的距离
定长
O
P
G
问题:点P是圆外的一个定点,点G是圆O上的一个动点, PG的最长距离和最短距离是多少?
知识储备
G1
G2
最长距离:
最短距离:
PG1
PG2
米
引例: 如图,长2米的梯子AB竖直放在墙角,在沿着墙角缓慢下滑直至水平地面过程中,梯子AB的中点P的移动轨迹长度为________.
由直角三角形斜边上的中线等于斜边的一半可知OP=1
=
动点到定点的距离
定长
变式1:在矩形 ABCD 中,AB=2,AD=3,点 E,F 分别为 AD、DC 边上的动点,且 EF=2, G 为 EF 的中点,P 为 BC 边上一动点,则 PA+PG 的最小值为 .
P''
G'
P'
2
2
3
P
A
G
4
变式2:在矩形 ABCD 中,已知 AB=2,BC=3,点 E 为边AB上的中点,点 F 是BC 边 上的动点,将△EBF沿EF所在的直线折叠得到△EB’F ,连接B’D,则B’D的 最小值是 .
B'
1
1
3
3
=
动点到定点的距离
定长
变式3:在平行四边形ABCD 中,∠BCD=30°,BC=4,CD= ,M 是 AD 边的中点,N 是 AB 边上一动点,将△AMN 沿 MN 所在直线翻折得到△A'MN,连接 MC,
则 A'C 长度的最小值是 。
2
2
A''
H
30°
1
=
动点到定点的距离
定长
5
变式4:在 Rt△ABC 中,∠C=90°,AC=6,BC=8,点 F 在边 AC 上,并且 CF=2,点 E 为边 BC 上的动点,将△CEF 沿直线 EF 翻折,点 C 落在点 P 处。
(1)点 P 到边 AB 距离的最小值是 。
变式: △ABP的面积的最小值是 。
H
P'
2
4
10
=
动点到定点的距离
定长
8
6
变式5:如图,等边△ABC中,AB=6,点D在BC上,BD=4,点E为边AC上一动点(不与点C重合),△CDE关于DE的轴对称图形为△FDE.(1)求△ABF的面积的最小值为 。
F'
H
6
例1:如图,等边△ABC中,AB=6,点D在BC上,BD=4,点E为边AC上一动点
(不与点C重合),△CDE关于DE的轴对称图形为△FDE.
设△ACD的面积为S1,△ABF的面积为S2,记S=S1-S2,
S是否存在最大值?若存在,求出S的最大值;
若不存在,请说明理由;
F'
H
4
2
2
6
2
G
6
例1:如图,等边△ABC中,AB=6,点D在BC上,BD=4,点E为边AC上一动点
(不与点C重合),△CDE关于DE的轴对称图形为△FDE.
设△ACD的面积为S1,△ABF的面积为S2,记S=S1-S2,
S是否存在最大值?若存在,求出S的最大值;
若不存在,请说明理由;
小结
模型三
模型二
模型一:动点到定点定长模型
课后思考题
同学们再见!
