2022中考专题 九年级下册第三章 圆 圆的有关概念与性质 课件(共18张PPT)
文档属性
| 名称 | 2022中考专题 九年级下册第三章 圆 圆的有关概念与性质 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-25 08:51:34 | ||
图片预览






文档简介
(共18张PPT)
圆的有关概念与性质
1、回顾并掌握圆的有关概念与性质
2、会根据圆的有关概念与性质解决圆中的问题
【学习目标】
(一)知识点1:点与圆的位置关系
【考点梳理】
若点P到圆心O的距离为d,r为半径,当P在圆外,则d_____r ; 当P在圆上,则d______r ; 当P在圆内,则d________r
>
=
<
(二)知识点2:圆的对称性
【考点梳理】
(1)圆的对称性:圆是_______对称图形,其对称轴__________________________ ;圆又是 _______ 对称图形,对称中心为 ______________ ;并且圆具有旋转不变性.
(2)在同圆或等圆中,如果两个圆心角、两条弧、两条_________中有一组量相等,那么它们所对应的其余各组量都分别相等.
轴
任意一条过圆心的直线
中心
圆心
弦
(三)知识点3:圆周角和圆心角的关系
【考点梳理】
(1)圆周角的度数等于它所对弧的__________度数的_______.
(2)同弧或等弧所对的圆周角__________.
(3)直径所对的圆周角是______度,90度的圆周角所对的弦是________
圆心角
一半
90
直径
相等
(四)知识点4:垂径定理
【考点梳理】
(1)垂直于弦的直径 _________,并且平分这条弦所对的两条___________
(2)平分弦(不是直径)的直径___________ 弦,并且平分弦所对的两条弧.
弧
平分弦
垂直于
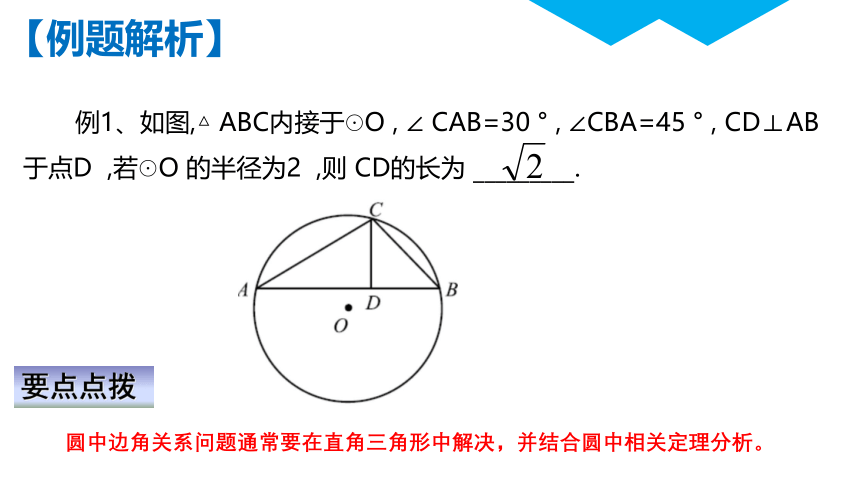
例1、如图,△ ABC内接于☉O , ∠ CAB=30 ° , ∠CBA=45 ° , CD⊥AB于点D ,若☉O 的半径为2 ,则 CD的长为 _________.
【例题解析】
要点点拨
圆中边角关系问题通常要在直角三角形中解决,并结合圆中相关定理分析。
例2、如图,已知⊙O的半径长为1,AB、AC是⊙O的两条弦,且AB=AC,BO的延长线交AC于点D,联结OA、OC.
(1)求证:△OAD∽△ABD;
(2)当△OCD是直角三角形时,求B、C两点的距离.
【例题解析】
例2、如图,已知⊙O的半径长为1,AB、AC是⊙O的两条弦,且AB=AC,BO的延长线交AC于点D,联结OA、OC.
(1)求证:△OAD∽△ABD;
(2)当△OCD是直角三角形时,求B、C两点的距离.
【例题解析】
例2、如图,已知⊙O的半径长为1,AB、AC是⊙O的两条弦,且AB=AC,BO的延长线交AC于点D,联结OA、OC.
(1)求证:△OAD∽△ABD;
(2)当△OCD是直角三角形时,求B、C两点的距离.
【例题解析】
【例题解析】
1、要熟练掌握圆中弦、弧、圆心角、圆周角的关系.
3、利用垂径定理进行计算或证明时,常需找到或者作出弦心距,则垂足为弦的中点,再连接半径,那就可以利用圆的半径、弦心距和弦的一半组成的直角三角形来求解.
2、半径相等是一个非常重要的隐含条件.
4、分类讨论的思想
要点点拨
例3、如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,且∠1=∠C (1)求证:CB//PD (2)若BC=3,sin∠P= ,求⊙O直径
【例题解析】
解题关键是理清垂径定理所涉及的弦、弧、圆心角以及出现的垂直之间的关系
要点点拨
通过本节课的学习,你掌握了哪些内容?
1、圆中有关概念与性质.
2、在解决圆中边和角的问题时,常常寻找或者建立直角三角形是解题的关键.
总结:
3、进一步的理解了数学的分类思想.
谢谢观看
圆的有关概念与性质
1、回顾并掌握圆的有关概念与性质
2、会根据圆的有关概念与性质解决圆中的问题
【学习目标】
(一)知识点1:点与圆的位置关系
【考点梳理】
若点P到圆心O的距离为d,r为半径,当P在圆外,则d_____r ; 当P在圆上,则d______r ; 当P在圆内,则d________r
>
=
<
(二)知识点2:圆的对称性
【考点梳理】
(1)圆的对称性:圆是_______对称图形,其对称轴__________________________ ;圆又是 _______ 对称图形,对称中心为 ______________ ;并且圆具有旋转不变性.
(2)在同圆或等圆中,如果两个圆心角、两条弧、两条_________中有一组量相等,那么它们所对应的其余各组量都分别相等.
轴
任意一条过圆心的直线
中心
圆心
弦
(三)知识点3:圆周角和圆心角的关系
【考点梳理】
(1)圆周角的度数等于它所对弧的__________度数的_______.
(2)同弧或等弧所对的圆周角__________.
(3)直径所对的圆周角是______度,90度的圆周角所对的弦是________
圆心角
一半
90
直径
相等
(四)知识点4:垂径定理
【考点梳理】
(1)垂直于弦的直径 _________,并且平分这条弦所对的两条___________
(2)平分弦(不是直径)的直径___________ 弦,并且平分弦所对的两条弧.
弧
平分弦
垂直于
例1、如图,△ ABC内接于☉O , ∠ CAB=30 ° , ∠CBA=45 ° , CD⊥AB于点D ,若☉O 的半径为2 ,则 CD的长为 _________.
【例题解析】
要点点拨
圆中边角关系问题通常要在直角三角形中解决,并结合圆中相关定理分析。
例2、如图,已知⊙O的半径长为1,AB、AC是⊙O的两条弦,且AB=AC,BO的延长线交AC于点D,联结OA、OC.
(1)求证:△OAD∽△ABD;
(2)当△OCD是直角三角形时,求B、C两点的距离.
【例题解析】
例2、如图,已知⊙O的半径长为1,AB、AC是⊙O的两条弦,且AB=AC,BO的延长线交AC于点D,联结OA、OC.
(1)求证:△OAD∽△ABD;
(2)当△OCD是直角三角形时,求B、C两点的距离.
【例题解析】
例2、如图,已知⊙O的半径长为1,AB、AC是⊙O的两条弦,且AB=AC,BO的延长线交AC于点D,联结OA、OC.
(1)求证:△OAD∽△ABD;
(2)当△OCD是直角三角形时,求B、C两点的距离.
【例题解析】
【例题解析】
1、要熟练掌握圆中弦、弧、圆心角、圆周角的关系.
3、利用垂径定理进行计算或证明时,常需找到或者作出弦心距,则垂足为弦的中点,再连接半径,那就可以利用圆的半径、弦心距和弦的一半组成的直角三角形来求解.
2、半径相等是一个非常重要的隐含条件.
4、分类讨论的思想
要点点拨
例3、如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,且∠1=∠C (1)求证:CB//PD (2)若BC=3,sin∠P= ,求⊙O直径
【例题解析】
解题关键是理清垂径定理所涉及的弦、弧、圆心角以及出现的垂直之间的关系
要点点拨
通过本节课的学习,你掌握了哪些内容?
1、圆中有关概念与性质.
2、在解决圆中边和角的问题时,常常寻找或者建立直角三角形是解题的关键.
总结:
3、进一步的理解了数学的分类思想.
谢谢观看
