北师大版九年级数学下册综合法证明(1)——特殊平行四边形综合题课件(共18张PPT)
文档属性
| 名称 | 北师大版九年级数学下册综合法证明(1)——特殊平行四边形综合题课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-25 09:51:38 | ||
图片预览

文档简介
(共18张PPT)
综合法证明(1)
----特殊平行四边形的综合题
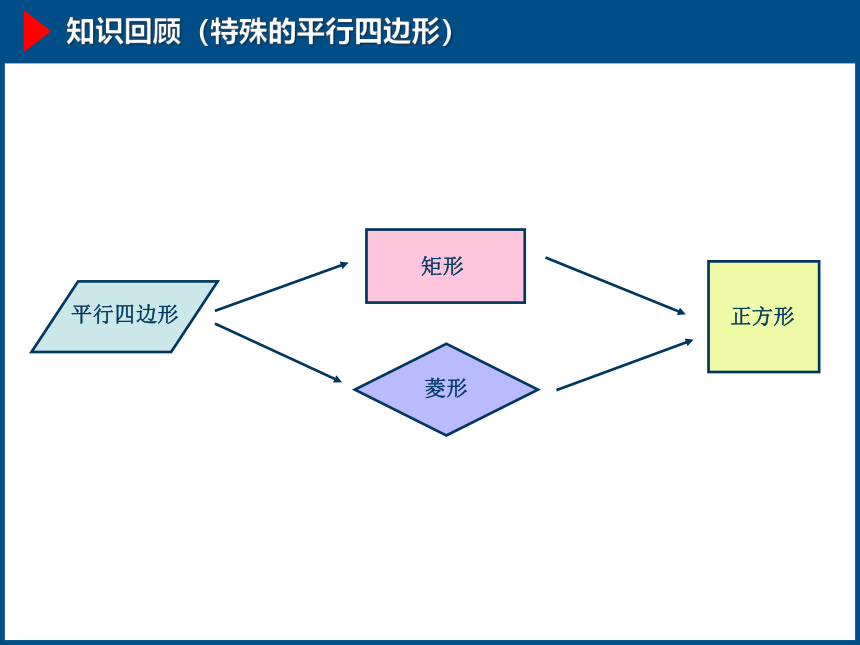
知识回顾(特殊的平行四边形)
平行四边形
矩形
菱形
正方形
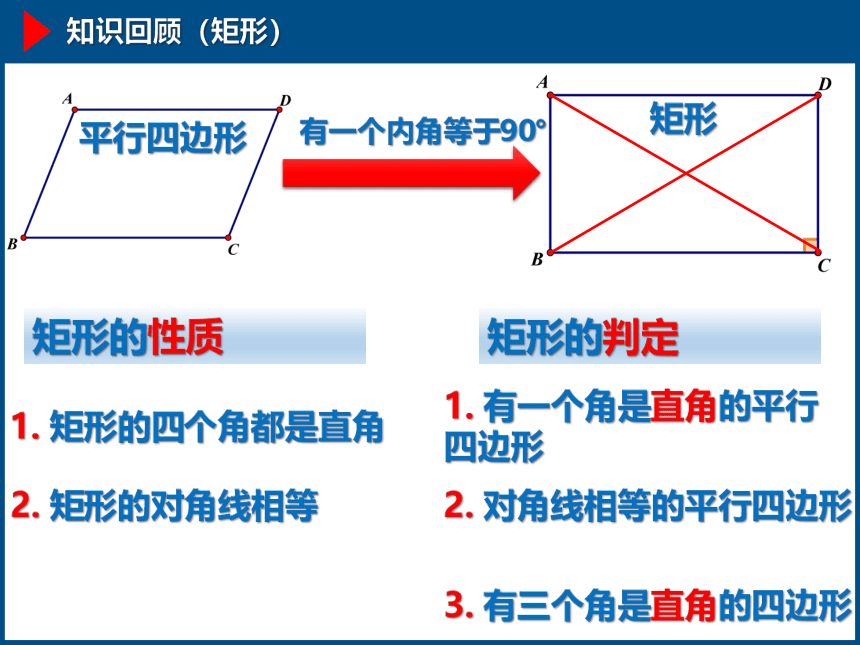
知识回顾(矩形)
平行四边形
有一个内角等于90°
矩形
矩形的性质
矩形的判定
1. 矩形的四个角都是直角
2. 矩形的对角线相等
1. 有一个角是直角的平行四边形
2. 对角线相等的平行四边形
3. 有三个角是直角的四边形
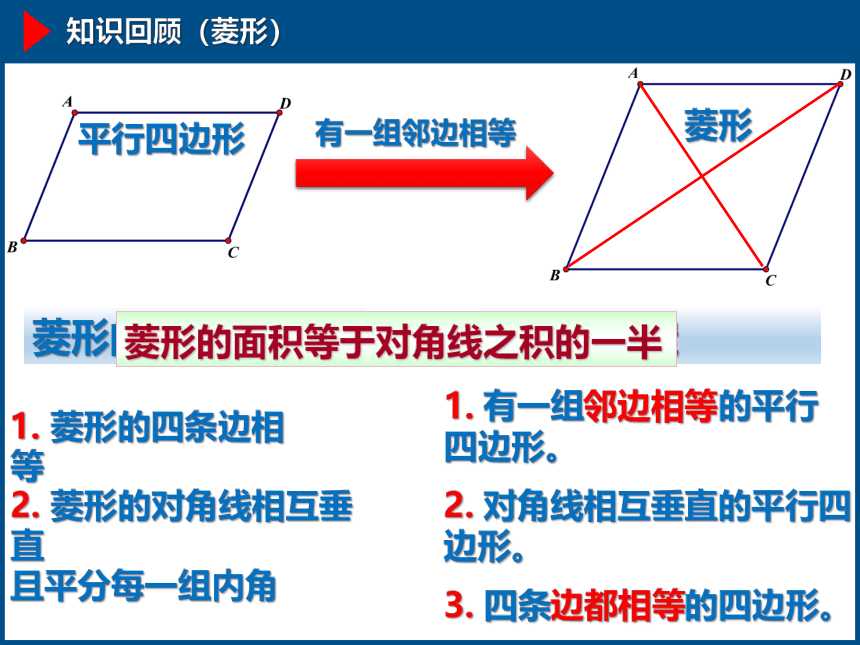
知识回顾(菱形)
平行四边形
有一组邻边相等
菱形
菱形的性质
菱形的判定
1. 菱形的四条边相等
2. 菱形的对角线相互垂直
且平分每一组内角
1. 有一组邻边相等的平行四边形。
2. 对角线相互垂直的平行四边形。
3. 四条边都相等的四边形。
菱形的面积等于对角线之积的一半
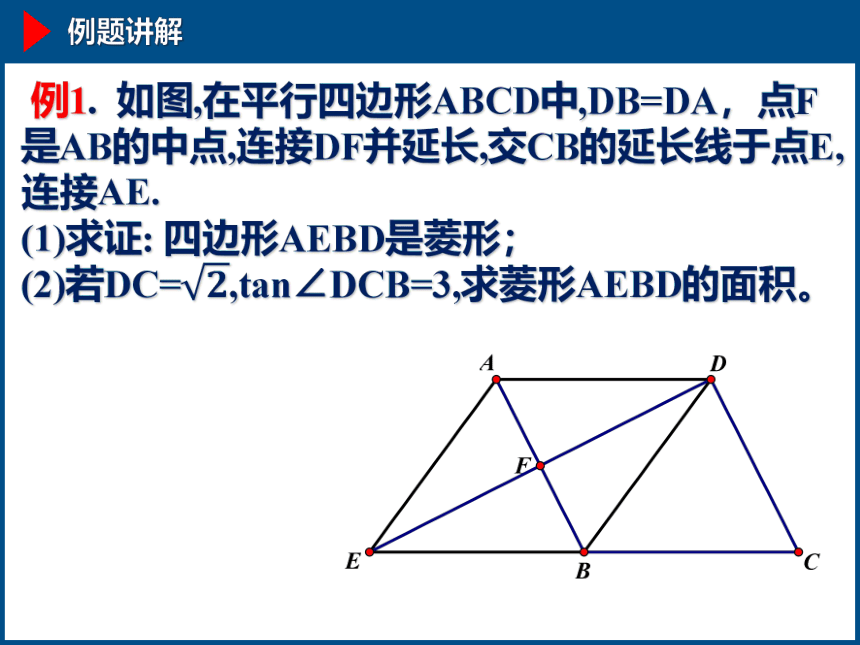
例题讲解
例1. 如图,在平行四边形ABCD中,DB=DA,点F是AB的中点,连接DF并延长,交CB的延长线于点E,连接AE.
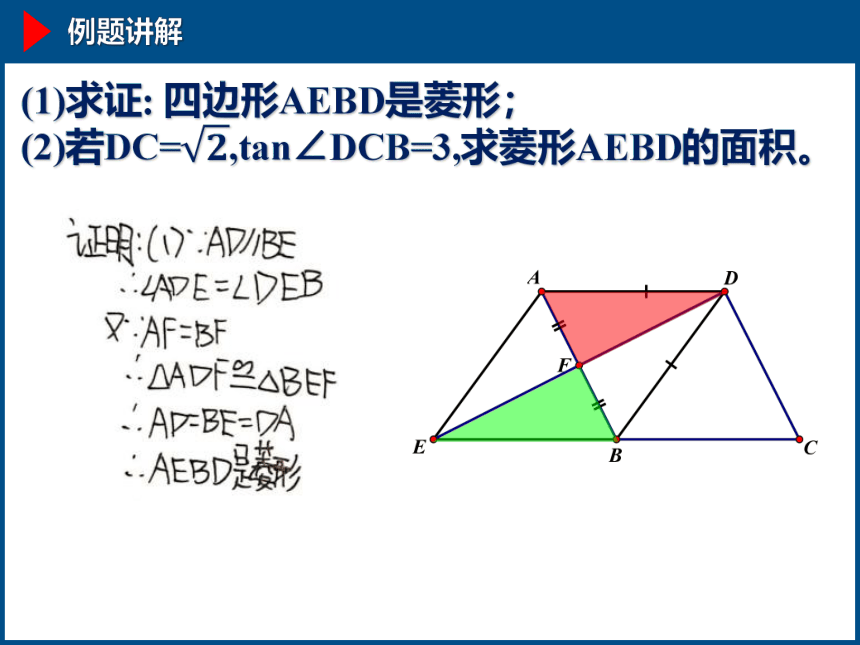
(1)求证: 四边形AEBD是菱形;
(2)若DC=,tan∠DCB=3,求菱形AEBD的面积。
例题讲解
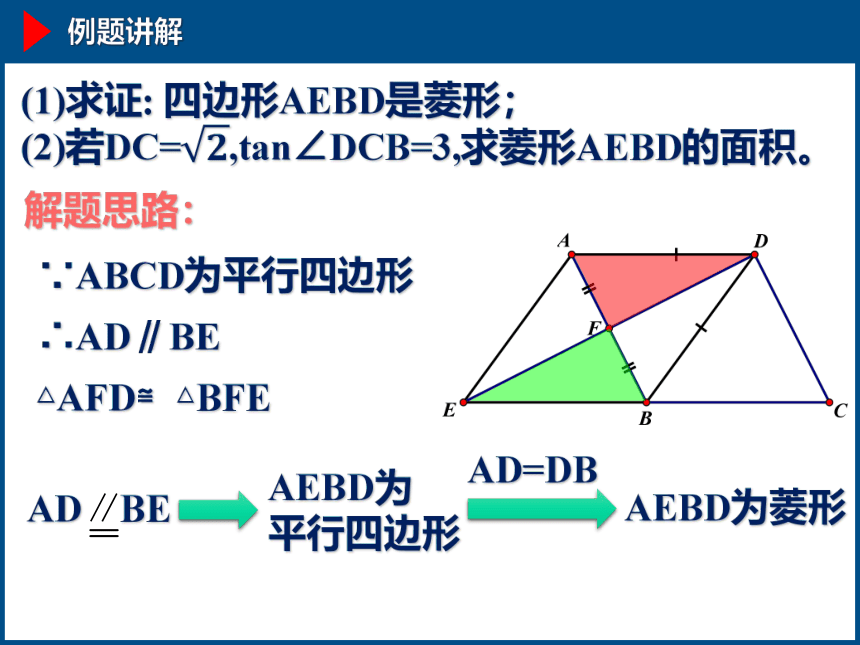
(1)求证: 四边形AEBD是菱形;
(2)若DC=,tan∠DCB=3,求菱形AEBD的面积。
△AFD≌△BFE
解题思路:
AEBD为
平行四边形
AEBD为菱形
AD=DB
∵ABCD为平行四边形
∴AD∥BE
AD BE
例题讲解
(1)求证: 四边形AEBD是菱形;
(2)若DC=,tan∠DCB=3,求菱形AEBD的面积。
例题讲解
(1)求证: 四边形AEBD是菱形;
(2)若DC=,tan∠DCB=3,求菱形AEBD的面积。
解题思路:
∴在RT△EDC中, ED=CDtan∠DCB=
∴∠EFB=∠EDC=90°
∵ABCD是平行四边形
∵AB∥CD
AB= DE=
∴AB=CD=
∵AEBD是菱形
∴∠EFB=90°
∴
深圳中考
2018年深圳中考 第20题
(1)求证:四边形ACDB为△FEC的亲密菱形;
(2)求四边形ACDB的面积。
已知菱形的一个角与三角形的一个角重合,然后它的对角顶点在这个重合角的对边上,这个菱形称为这个三角形的亲密菱形, 如图, 在△CFE中, CF=6, CE=12, ∠FCE=45°, 以点C为圆心, 以任意长为半径作AD, 再分别以点A和点D为圆心, 大于AD长为半径作弧, 交EF于点B, AB∥CD.
深圳中考
2018年深圳中考 第20题
(1)求证:四边形ACDB为△FEC的亲密菱形;
(2)求四边形ACDB的面积。
证明:
由题意得:AC=DC, AB=BD
由尺规作图得:CB平分∠FCE
∴∠ACB=∠DCB
∵AB∥CD
∴∠ABC=∠ACB
∴∠ACB=∠ABC
∴AB=AC
∴AB=BD=DC=CA
∴四边形ACDB为菱形
∵∠ACD与△FEC中的∠FCE重合,它的对角∠ABD顶点在EF上
∴四边形ACDB为△FEC的亲密菱形
深圳中考
2018年深圳中考 第20题
(2)求四边形ACDB的面积。
设AB = AC = x
x
x
6
12
∵AB∥CE
∴
,则AF = 6-x
∴
∴解得 x = 4
∵ACDB为菱形
∴AC=CD=4
∵∠ACH=45°, AC=4
∴ 在RT△ACH中,
AH=ACsin∠ACH= 4
作AH⊥CD于点H
∴
∴△AFB∽CFE
深圳中考
2012年深圳中考
2014年深圳中考
2018年深圳中考
一证一算
(1)求证:四边形
AFCE为菱形
(2)设AE=a,ED=b,
DC=c,请写出一个
a,b,c三者之间的
数量关系式。
(1)求证:四边形ABDF为平行四边形。
(2)若AE=DF=5, AD=6, 求AC的长。
(1)求证:四边形ACDB为△FEC的亲密菱形;
(2)求四边形ACDB的面积。
1. 注意书写,不要跳步
2. 熟练应用三角形相似,全等或解直角三角形的知识解决问题。
能力提升
例2. 如图,在△ABC中,D是AB上一点,DE⊥AC于点E,F是AD的中点,FG⊥BC于点G,与DE交于点H,若FG=AF,AG平分∠CAB,连接GE,GD.
(1)求证:△ECG≌△GHD;
(2)若∠B=30°,求证:四边形AEGF为菱形。
(3)求证:AD=AC+EC.
能力提升
(1)求证:△ECG≌△GHD;
AC∥FG
解题思路:
∠1=∠2
AF=FG
1
2
AF=FD,
FG∥AE,
FG⊥ED
FG为中垂线
∠HEC=∠ECG =∠EHG=90°
EHGC为矩形
∠ECG =∠GHD=90°
EC=HG
EG=GD
△ECG≌△GHD
能力提升
(2)若∠B=30°,求证:四边形AEGF为菱形。
∵ED∥BC, ∠B=30°
∴∠ADE=30°
∵∠AED=90°
∴
∵AE=FG, AE∥FG
∴AEGF为平行四边形
∵AF=FG
∴AEGF为菱形
能力提升
(3)求证:AD=AC+EC.
AC=AK
解题思路:
∠1=∠2
GC⊥AC
1
2
∠ECG =∠GKD=90°
GK=GC
EG=GD
△ECG≌△DKG
GK⊥AB
AD=AK+KD=AC+EC
能力提升
(3)求证:AD=AC+EC.
AK=AD
解题思路:
∠1=∠2
AG⊥DK
1
2
GK=GD
EG=GD
GE=GK
AD=AK=AC+CK=AC+EC
GE=GK
GC⊥EK
CK=CE
AD=AC+EC
特殊平行四边形综合题
谢谢聆听!
综合法证明(1)
----特殊平行四边形的综合题
知识回顾(特殊的平行四边形)
平行四边形
矩形
菱形
正方形
知识回顾(矩形)
平行四边形
有一个内角等于90°
矩形
矩形的性质
矩形的判定
1. 矩形的四个角都是直角
2. 矩形的对角线相等
1. 有一个角是直角的平行四边形
2. 对角线相等的平行四边形
3. 有三个角是直角的四边形
知识回顾(菱形)
平行四边形
有一组邻边相等
菱形
菱形的性质
菱形的判定
1. 菱形的四条边相等
2. 菱形的对角线相互垂直
且平分每一组内角
1. 有一组邻边相等的平行四边形。
2. 对角线相互垂直的平行四边形。
3. 四条边都相等的四边形。
菱形的面积等于对角线之积的一半
例题讲解
例1. 如图,在平行四边形ABCD中,DB=DA,点F是AB的中点,连接DF并延长,交CB的延长线于点E,连接AE.
(1)求证: 四边形AEBD是菱形;
(2)若DC=,tan∠DCB=3,求菱形AEBD的面积。
例题讲解
(1)求证: 四边形AEBD是菱形;
(2)若DC=,tan∠DCB=3,求菱形AEBD的面积。
△AFD≌△BFE
解题思路:
AEBD为
平行四边形
AEBD为菱形
AD=DB
∵ABCD为平行四边形
∴AD∥BE
AD BE
例题讲解
(1)求证: 四边形AEBD是菱形;
(2)若DC=,tan∠DCB=3,求菱形AEBD的面积。
例题讲解
(1)求证: 四边形AEBD是菱形;
(2)若DC=,tan∠DCB=3,求菱形AEBD的面积。
解题思路:
∴在RT△EDC中, ED=CDtan∠DCB=
∴∠EFB=∠EDC=90°
∵ABCD是平行四边形
∵AB∥CD
AB= DE=
∴AB=CD=
∵AEBD是菱形
∴∠EFB=90°
∴
深圳中考
2018年深圳中考 第20题
(1)求证:四边形ACDB为△FEC的亲密菱形;
(2)求四边形ACDB的面积。
已知菱形的一个角与三角形的一个角重合,然后它的对角顶点在这个重合角的对边上,这个菱形称为这个三角形的亲密菱形, 如图, 在△CFE中, CF=6, CE=12, ∠FCE=45°, 以点C为圆心, 以任意长为半径作AD, 再分别以点A和点D为圆心, 大于AD长为半径作弧, 交EF于点B, AB∥CD.
深圳中考
2018年深圳中考 第20题
(1)求证:四边形ACDB为△FEC的亲密菱形;
(2)求四边形ACDB的面积。
证明:
由题意得:AC=DC, AB=BD
由尺规作图得:CB平分∠FCE
∴∠ACB=∠DCB
∵AB∥CD
∴∠ABC=∠ACB
∴∠ACB=∠ABC
∴AB=AC
∴AB=BD=DC=CA
∴四边形ACDB为菱形
∵∠ACD与△FEC中的∠FCE重合,它的对角∠ABD顶点在EF上
∴四边形ACDB为△FEC的亲密菱形
深圳中考
2018年深圳中考 第20题
(2)求四边形ACDB的面积。
设AB = AC = x
x
x
6
12
∵AB∥CE
∴
,则AF = 6-x
∴
∴解得 x = 4
∵ACDB为菱形
∴AC=CD=4
∵∠ACH=45°, AC=4
∴ 在RT△ACH中,
AH=ACsin∠ACH= 4
作AH⊥CD于点H
∴
∴△AFB∽CFE
深圳中考
2012年深圳中考
2014年深圳中考
2018年深圳中考
一证一算
(1)求证:四边形
AFCE为菱形
(2)设AE=a,ED=b,
DC=c,请写出一个
a,b,c三者之间的
数量关系式。
(1)求证:四边形ABDF为平行四边形。
(2)若AE=DF=5, AD=6, 求AC的长。
(1)求证:四边形ACDB为△FEC的亲密菱形;
(2)求四边形ACDB的面积。
1. 注意书写,不要跳步
2. 熟练应用三角形相似,全等或解直角三角形的知识解决问题。
能力提升
例2. 如图,在△ABC中,D是AB上一点,DE⊥AC于点E,F是AD的中点,FG⊥BC于点G,与DE交于点H,若FG=AF,AG平分∠CAB,连接GE,GD.
(1)求证:△ECG≌△GHD;
(2)若∠B=30°,求证:四边形AEGF为菱形。
(3)求证:AD=AC+EC.
能力提升
(1)求证:△ECG≌△GHD;
AC∥FG
解题思路:
∠1=∠2
AF=FG
1
2
AF=FD,
FG∥AE,
FG⊥ED
FG为中垂线
∠HEC=∠ECG =∠EHG=90°
EHGC为矩形
∠ECG =∠GHD=90°
EC=HG
EG=GD
△ECG≌△GHD
能力提升
(2)若∠B=30°,求证:四边形AEGF为菱形。
∵ED∥BC, ∠B=30°
∴∠ADE=30°
∵∠AED=90°
∴
∵AE=FG, AE∥FG
∴AEGF为平行四边形
∵AF=FG
∴AEGF为菱形
能力提升
(3)求证:AD=AC+EC.
AC=AK
解题思路:
∠1=∠2
GC⊥AC
1
2
∠ECG =∠GKD=90°
GK=GC
EG=GD
△ECG≌△DKG
GK⊥AB
AD=AK+KD=AC+EC
能力提升
(3)求证:AD=AC+EC.
AK=AD
解题思路:
∠1=∠2
AG⊥DK
1
2
GK=GD
EG=GD
GE=GK
AD=AK=AC+CK=AC+EC
GE=GK
GC⊥EK
CK=CE
AD=AC+EC
特殊平行四边形综合题
谢谢聆听!
