2021-2022学年北师大版数学九年级下册3.4圆周角与圆心角的关系(第1课时)课件(共22张PPT)
文档属性
| 名称 | 2021-2022学年北师大版数学九年级下册3.4圆周角与圆心角的关系(第1课时)课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 843.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 17:57:33 | ||
图片预览





文档简介
(共22张PPT)
北师大版数学九年级(下)
4.圆周角与圆心角的关系
第三章 圆
1
第1课时 圆周角定理及其推论1
教学目标
重点难点
2.综合利用理解圆周角定理及其推论解决问题。(难点)
2
1.认识圆周角,理解并掌握圆周角定理及其推论1。(重点)
3
答一答
教学过程
温故知新
1.上什么叫圆心角?
顶点在圆心,两边和圆相交的角叫做圆心角。
2.同圆或等圆中圆心角、弧、弦、弦心距之间有什么关系?
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦心距相等。
议一议
教学过程
新课引入
4
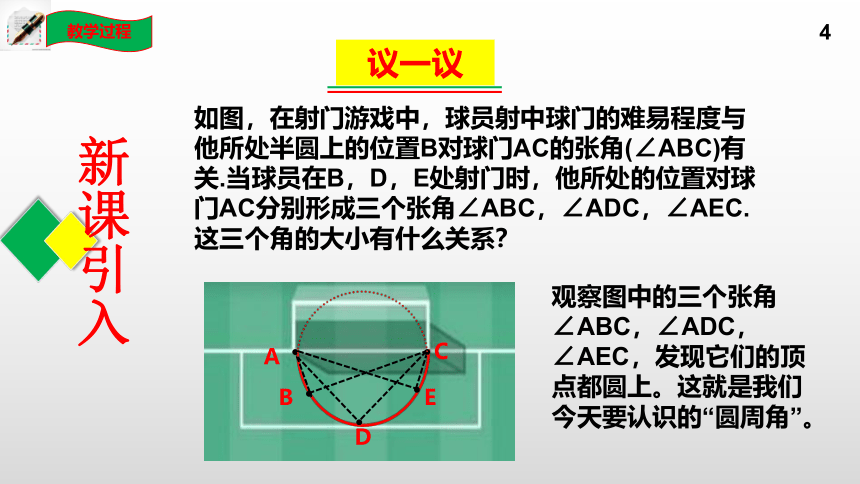
如图,在射门游戏中,球员射中球门的难易程度与他所处半圆上的位置B对球门AC的张角(∠ABC)有关.当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠AEC.这三个角的大小有什么关系?
A
B
C
E
D
观察图中的三个张角∠ABC,∠ADC,∠AEC,发现它们的顶点都圆上。这就是我们今天要认识的“圆周角”。
记一记
教学过程
新知新授
5
圆周角的概念
如右图,∠ABC,∠ADC,∠AEC,它们的顶点都圆上,角的两边和圆相交。
定义:顶点在圆上,两边和圆相交的角叫做圆周角。
理解:1.圆周角可以锐角、直角和钝角。
2.圆周角与圆心角的区别在于顶点位置不同。
议一议
教学过程
新知新授
7
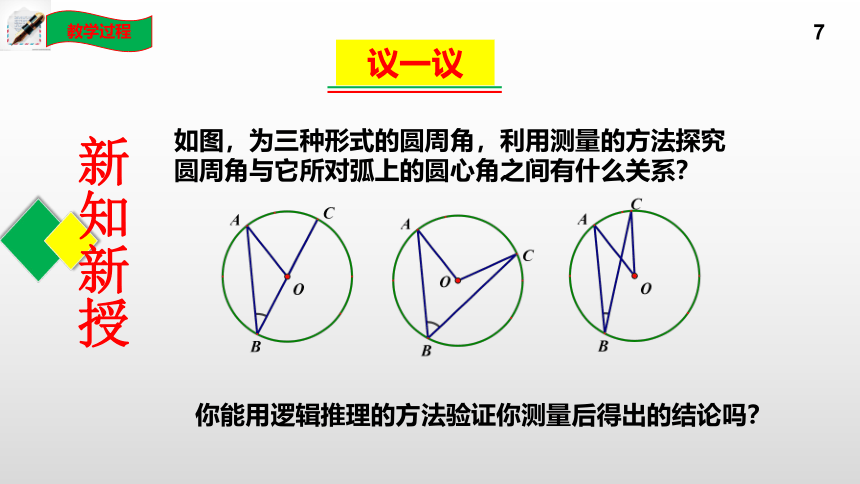
如图,为三种形式的圆周角,利用测量的方法探究圆周角与它所对弧上的圆心角之间有什么关系?
你能用逻辑推理的方法验证你测量后得出的结论吗?
议一议
教学过程
新知新授
6
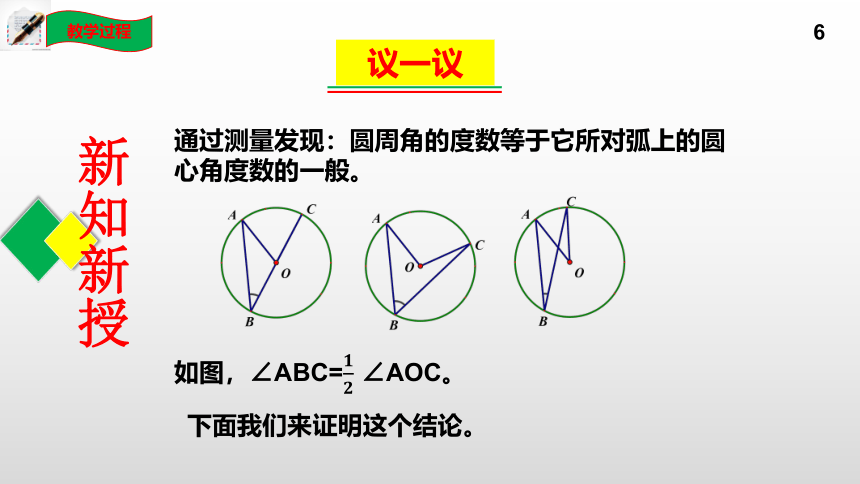
通过测量发现:圆周角的度数等于它所对弧上的圆心角度数的一般。
如图,∠ABC= ∠AOC。
下面我们来证明这个结论。
做一做
教学过程
新知新授
8
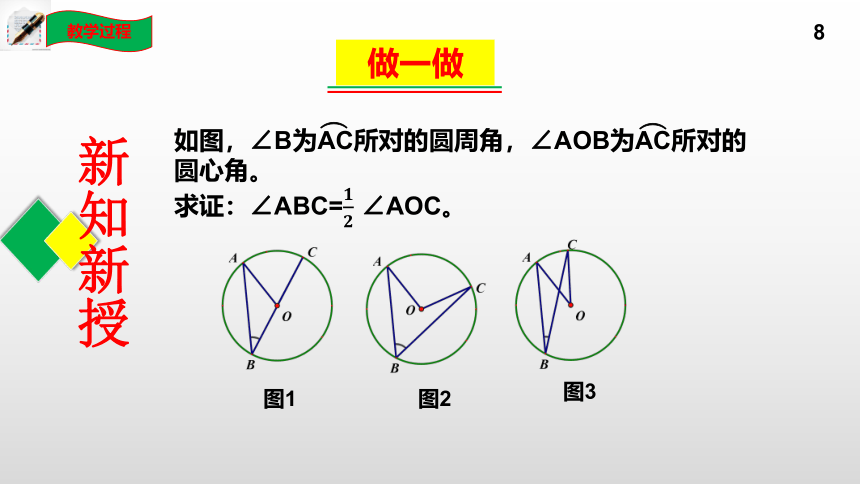
图1
图2
图3
如图,∠B为AC所对的圆周角,∠AOB为AC所对的圆心角。
求证:∠ABC= ∠AOC。
⌒
⌒
做一做
教学过程
回归课本
9
认真阅读课本第79页关于圆周角与圆心角关系的第一种情况的证明过程。
做一做
教学过程
新知新授
10
图2
利用图2来证明。
证明:连接BO并延长与⊙O相交于点D;
D
∵AOD是△AOB的外角,∴∠AOD=∠A+∠ABO
∵OA=OB, ∴∠A=∠ABO.
∴∠AOD=2∠ABO,
同理∠COD=2∠CBO,
∴∠AOD=2∠ABO,
∵∠AOC=∠AOD+∠COD,∠ABC=∠ABO+∠CBO.
∴∠AOC=2∠ABO+2∠CBO=2∠ABC.
∴∠ABC=∠AOC
做一做
教学过程
新知新授
10
图3
利用图3来证明。
证明:连接BO并延长与⊙O相交于点D;
D
由前面的证明可知
∠ABD=∠AOD
∠CBD=∠COD
∵∠ABC=∠ABD-∠COD,∠AOC=∠AOD-∠COD.
∴∠ABC=∠AOD-∠COD=∠AOC.
记一记
教学过程
新知新授
12
圆周角定理
通过前面的探究可知,圆周角具有如下性质:
圆周角定理 :圆周角的度数等于它所对弧上的圆心角度数的一半.
符号语言 :在⊙O中,∵∠ABC是圆周角,
∠AOC是圆心角,∴∠ABC=∠AOC.
理解:不能把定理中的“它所对孤上的”去掉,而简单说成圆周角的度数等于圆心角度数的一半”,也不能把“它所对孤上的”改为“它所对弦上的”,这是因为一条弦所对的圆周角有两种情况,它们分别位于这条弦的两侧.
做一做
教学过程
现学现用
13
如图,A、B、C是⊙O上的三点,∠ACB=25°,则∠BAO的度数是( )
A.55° B.60° C.65° D.70°
C
议一议
教学过程
新知新授
14
A
B
如图,在⊙O中,AB所对的圆心角你能画几个?AB所对的圆周角能画几个?
⌒
⌒
只能画一个圆心角∠AOB;
C
D
E
可以画出∠ACB、∠ADB、∠AEB等多个圆周角。
圆周角∠ACB、∠ADB、∠AEB的大小有什么关系?
记一记
教学过程
新知新授
15
圆周角定理的推论1
A
B
C
D
E
利用圆周角定理很容易知道:
∠ACB=∠ADB=∠AEB=∠AOB
⌒
圆周角定理推论1:同弧或等弧所对的圆周角相等.
⌒
符号语言 :在⊙O中,∵∠ACB、∠ADB、∠AEB是AB所对的圆周角,∴∠ACB=∠ADB=∠AEB.
做一做
教学过程
现学现用
16
如图所示,A、B、C都是⊙O上的点,D是⊙O外一点。连结AC、AD、BC、BD,比较∠C与∠D的大小,下列结论正确的是( )
A.∠C>∠D
B.∠C=∠D
C.∠C<∠D
D.∠C与∠D大小关系不能确定
A
做一做
教学过程
例题解析
17
如图,OA、OB是⊙O的半径且OA⊥OB,作OA的垂直平分线交⊙O于点C、D,连结CB、AB.
求证:∠ABC=2∠CBO.
做一做
教学过程
例题解析
18
证明连结OC、AC.
∵CD垂直平分OA ,∴OC=AC,∴OC=AC=OA,
∴△OAC是等边三角形,∴∠AOC=60°
∴∠ABC=∠AOC=30°.
∵CO⊥OB, ∴∠AOB=90°,
∴∠BOC=∠AOC+∠AOB=150°.
又∵OB=OC,
∴∠CBO=(180°-∠BOC)=15°,
∴∠ABC=2∠CBO.
做一做
教学过程
随堂练习
19
完成课本第80页“随堂练习”
记一记
教学过程
课堂小结
20
圆周角定理 :圆周角的度数等于它所对弧上的圆心角度数的一半.
圆周角定理推论1:同弧或等弧所对的圆周角相等.
做一做
教学过程
课后巩固
21
第一层:课本第80页习题3.4第1、2题
第一层:课本第80页习题3.4第1、2、4题
教学过程
结束新课
感谢聆听
22
北师大版数学九年级(下)
4.圆周角与圆心角的关系
第三章 圆
1
第1课时 圆周角定理及其推论1
教学目标
重点难点
2.综合利用理解圆周角定理及其推论解决问题。(难点)
2
1.认识圆周角,理解并掌握圆周角定理及其推论1。(重点)
3
答一答
教学过程
温故知新
1.上什么叫圆心角?
顶点在圆心,两边和圆相交的角叫做圆心角。
2.同圆或等圆中圆心角、弧、弦、弦心距之间有什么关系?
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦心距相等。
议一议
教学过程
新课引入
4
如图,在射门游戏中,球员射中球门的难易程度与他所处半圆上的位置B对球门AC的张角(∠ABC)有关.当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠AEC.这三个角的大小有什么关系?
A
B
C
E
D
观察图中的三个张角∠ABC,∠ADC,∠AEC,发现它们的顶点都圆上。这就是我们今天要认识的“圆周角”。
记一记
教学过程
新知新授
5
圆周角的概念
如右图,∠ABC,∠ADC,∠AEC,它们的顶点都圆上,角的两边和圆相交。
定义:顶点在圆上,两边和圆相交的角叫做圆周角。
理解:1.圆周角可以锐角、直角和钝角。
2.圆周角与圆心角的区别在于顶点位置不同。
议一议
教学过程
新知新授
7
如图,为三种形式的圆周角,利用测量的方法探究圆周角与它所对弧上的圆心角之间有什么关系?
你能用逻辑推理的方法验证你测量后得出的结论吗?
议一议
教学过程
新知新授
6
通过测量发现:圆周角的度数等于它所对弧上的圆心角度数的一般。
如图,∠ABC= ∠AOC。
下面我们来证明这个结论。
做一做
教学过程
新知新授
8
图1
图2
图3
如图,∠B为AC所对的圆周角,∠AOB为AC所对的圆心角。
求证:∠ABC= ∠AOC。
⌒
⌒
做一做
教学过程
回归课本
9
认真阅读课本第79页关于圆周角与圆心角关系的第一种情况的证明过程。
做一做
教学过程
新知新授
10
图2
利用图2来证明。
证明:连接BO并延长与⊙O相交于点D;
D
∵AOD是△AOB的外角,∴∠AOD=∠A+∠ABO
∵OA=OB, ∴∠A=∠ABO.
∴∠AOD=2∠ABO,
同理∠COD=2∠CBO,
∴∠AOD=2∠ABO,
∵∠AOC=∠AOD+∠COD,∠ABC=∠ABO+∠CBO.
∴∠AOC=2∠ABO+2∠CBO=2∠ABC.
∴∠ABC=∠AOC
做一做
教学过程
新知新授
10
图3
利用图3来证明。
证明:连接BO并延长与⊙O相交于点D;
D
由前面的证明可知
∠ABD=∠AOD
∠CBD=∠COD
∵∠ABC=∠ABD-∠COD,∠AOC=∠AOD-∠COD.
∴∠ABC=∠AOD-∠COD=∠AOC.
记一记
教学过程
新知新授
12
圆周角定理
通过前面的探究可知,圆周角具有如下性质:
圆周角定理 :圆周角的度数等于它所对弧上的圆心角度数的一半.
符号语言 :在⊙O中,∵∠ABC是圆周角,
∠AOC是圆心角,∴∠ABC=∠AOC.
理解:不能把定理中的“它所对孤上的”去掉,而简单说成圆周角的度数等于圆心角度数的一半”,也不能把“它所对孤上的”改为“它所对弦上的”,这是因为一条弦所对的圆周角有两种情况,它们分别位于这条弦的两侧.
做一做
教学过程
现学现用
13
如图,A、B、C是⊙O上的三点,∠ACB=25°,则∠BAO的度数是( )
A.55° B.60° C.65° D.70°
C
议一议
教学过程
新知新授
14
A
B
如图,在⊙O中,AB所对的圆心角你能画几个?AB所对的圆周角能画几个?
⌒
⌒
只能画一个圆心角∠AOB;
C
D
E
可以画出∠ACB、∠ADB、∠AEB等多个圆周角。
圆周角∠ACB、∠ADB、∠AEB的大小有什么关系?
记一记
教学过程
新知新授
15
圆周角定理的推论1
A
B
C
D
E
利用圆周角定理很容易知道:
∠ACB=∠ADB=∠AEB=∠AOB
⌒
圆周角定理推论1:同弧或等弧所对的圆周角相等.
⌒
符号语言 :在⊙O中,∵∠ACB、∠ADB、∠AEB是AB所对的圆周角,∴∠ACB=∠ADB=∠AEB.
做一做
教学过程
现学现用
16
如图所示,A、B、C都是⊙O上的点,D是⊙O外一点。连结AC、AD、BC、BD,比较∠C与∠D的大小,下列结论正确的是( )
A.∠C>∠D
B.∠C=∠D
C.∠C<∠D
D.∠C与∠D大小关系不能确定
A
做一做
教学过程
例题解析
17
如图,OA、OB是⊙O的半径且OA⊥OB,作OA的垂直平分线交⊙O于点C、D,连结CB、AB.
求证:∠ABC=2∠CBO.
做一做
教学过程
例题解析
18
证明连结OC、AC.
∵CD垂直平分OA ,∴OC=AC,∴OC=AC=OA,
∴△OAC是等边三角形,∴∠AOC=60°
∴∠ABC=∠AOC=30°.
∵CO⊥OB, ∴∠AOB=90°,
∴∠BOC=∠AOC+∠AOB=150°.
又∵OB=OC,
∴∠CBO=(180°-∠BOC)=15°,
∴∠ABC=2∠CBO.
做一做
教学过程
随堂练习
19
完成课本第80页“随堂练习”
记一记
教学过程
课堂小结
20
圆周角定理 :圆周角的度数等于它所对弧上的圆心角度数的一半.
圆周角定理推论1:同弧或等弧所对的圆周角相等.
做一做
教学过程
课后巩固
21
第一层:课本第80页习题3.4第1、2题
第一层:课本第80页习题3.4第1、2、4题
教学过程
结束新课
感谢聆听
22
