2022年高三数学二轮专题复习-优化解析几何运算策略(21张)
文档属性
| 名称 | 2022年高三数学二轮专题复习-优化解析几何运算策略(21张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 08:56:46 | ||
图片预览





文档简介
(共21张PPT)
优化解析几何
运算的策略
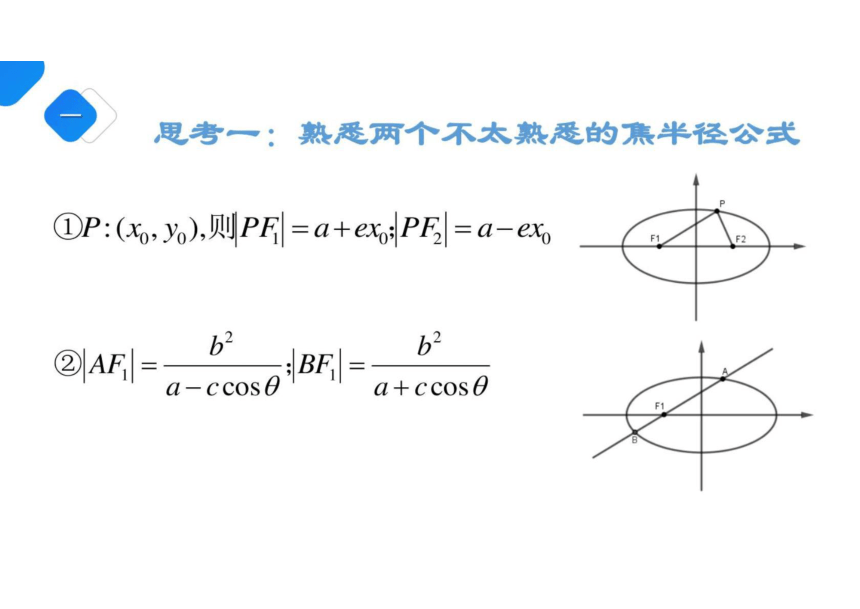
思考一:熟是两个不太熟是的集半径公式
①P:(x,y),则PF=a+ePF=a-e
b
2AF
a-CCosB78E - b2
a+ccos e
例
5.(2021年全国新高考1卷)已知F,F2是椭圆C:x+2=1的两个焦点,点M在C上,则MME
4
的最大值为()
A.13
B.12
C.9
D.6
(3+ex0(3-ex)=9-ex≤9
5.(2021年全国高考甲卷数学(理)已知F1,F2是双曲线C的两
∠FPE2=609PF=3PF,则C的离心率为()
C
a+exo=3(a-exo)
15.(2021年全国高考甲卷数学(理))已知F1,F2为椭圆C:
+y2
1的两个焦点,P,Q为C上关于坐
164
标原点对称的两点,且PQ=FF,则四边形PFQF的面积为
32
∠F1PF2=90,(4+ex)2+(4-ex)2=4c,
,S=(4-ex0)(4+ex)=8
3
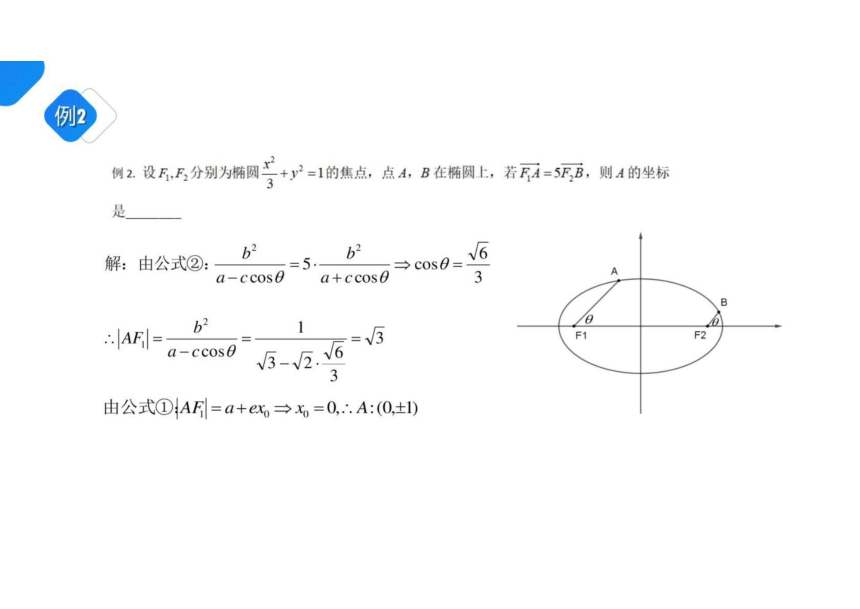
例
例2.设F1,F2分别为椭圆+y2=1的焦点,点A,B在椭圆上,若FA=5F2B,则A的坐标
是
解:由公式②:
b
b
=5
→cos
a-ccos8 a+ccos e
B
∴AF
F1
a-ccos日
0
由公式①AF=a+cx→石=0.A:(O士1)
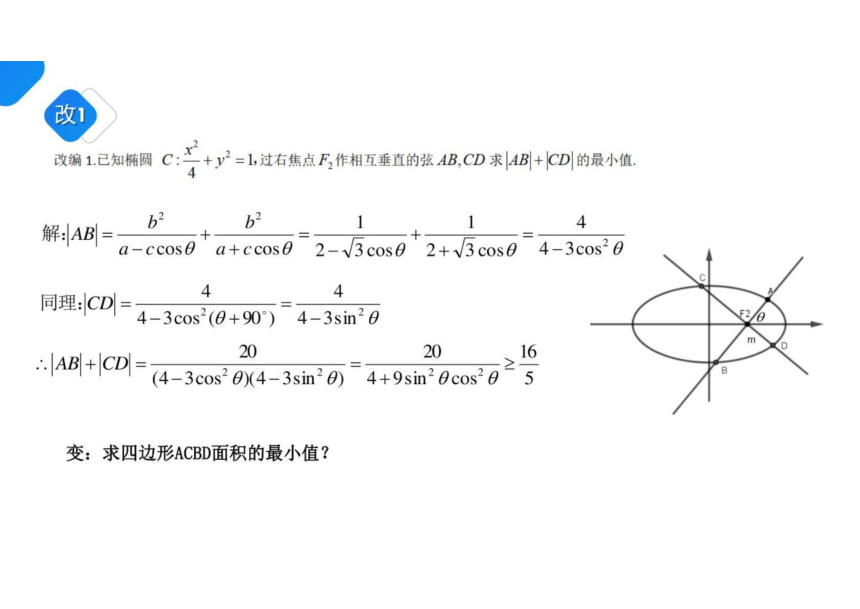
改1
改编1.已知椭圆C:
4y2=,过右焦点F2作相互垂直的弦AB,CD求B+CD的最小值
解AB=
b
b
4
a- coso a+ ccos 02-√3cos02+√3cos04-3cos20
同理CD
4
4-3cos(0+90)4-3sin 6
m
20
20
16
∴AB+CD=
(4-3cos 0 (4-3sin 0)4+sin*0 6 5
变:求四边形ACBD面积的最小值
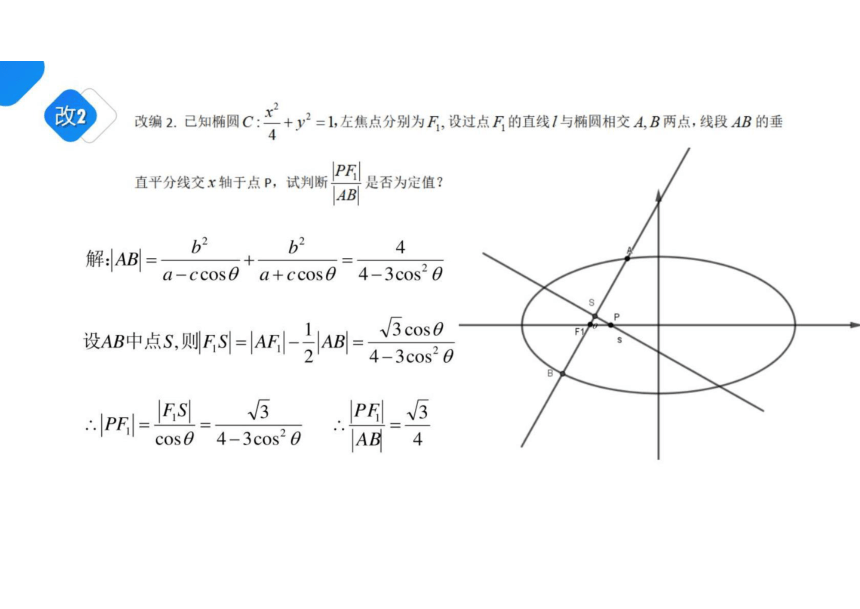
改
2)改编2.已知椭园C:+y2=1,左焦点分别为F,设过点F的直线与椭圆相交AB两点,线段AB的垂
PF
直平分线交x轴于点P,试判断上是否为定值
AB
b
4
解:AB
a-ccose a+ccos6 4-3cos6
设AB中点S则FS=AF|-AB
cos 0
4-3c0s20
PF=13
√PF√3
cos 8 4-3c0s 8 AB 4
例1
思考二:头注运算本质化繁为简
椭圆x+x=1(>b>0离心率为,长轴端点与短轴端点的距离为√5
(1)求椭圆的方程;
4
(2)经过D(,4)的直线与椭圆C交于两点E,F,O为坐标原点,若△OEF为直
角三角形,求直线l的斜率
直线与曲线交点一直线与直线的交点
解:设E(x1,y),F(x2,y2);
①∠EOF=90,x2+yy2=0→k=√19
4k4
②∠OEF=9
OE·y
k→E:
EF: y=kx+4
k2+1k2+
-4k
将E代入椭圆:k2+1+(4)2=1→k=±√5
k2+1
优化解析几何
运算的策略
思考一:熟是两个不太熟是的集半径公式
①P:(x,y),则PF=a+ePF=a-e
b
2AF
a-CCosB78E - b2
a+ccos e
例
5.(2021年全国新高考1卷)已知F,F2是椭圆C:x+2=1的两个焦点,点M在C上,则MME
4
的最大值为()
A.13
B.12
C.9
D.6
(3+ex0(3-ex)=9-ex≤9
5.(2021年全国高考甲卷数学(理)已知F1,F2是双曲线C的两
∠FPE2=609PF=3PF,则C的离心率为()
C
a+exo=3(a-exo)
15.(2021年全国高考甲卷数学(理))已知F1,F2为椭圆C:
+y2
1的两个焦点,P,Q为C上关于坐
164
标原点对称的两点,且PQ=FF,则四边形PFQF的面积为
32
∠F1PF2=90,(4+ex)2+(4-ex)2=4c,
,S=(4-ex0)(4+ex)=8
3
例
例2.设F1,F2分别为椭圆+y2=1的焦点,点A,B在椭圆上,若FA=5F2B,则A的坐标
是
解:由公式②:
b
b
=5
→cos
a-ccos8 a+ccos e
B
∴AF
F1
a-ccos日
0
由公式①AF=a+cx→石=0.A:(O士1)
改1
改编1.已知椭圆C:
4y2=,过右焦点F2作相互垂直的弦AB,CD求B+CD的最小值
解AB=
b
b
4
a- coso a+ ccos 02-√3cos02+√3cos04-3cos20
同理CD
4
4-3cos(0+90)4-3sin 6
m
20
20
16
∴AB+CD=
(4-3cos 0 (4-3sin 0)4+sin*0 6 5
变:求四边形ACBD面积的最小值
改
2)改编2.已知椭园C:+y2=1,左焦点分别为F,设过点F的直线与椭圆相交AB两点,线段AB的垂
PF
直平分线交x轴于点P,试判断上是否为定值
AB
b
4
解:AB
a-ccose a+ccos6 4-3cos6
设AB中点S则FS=AF|-AB
cos 0
4-3c0s20
PF=13
√PF√3
cos 8 4-3c0s 8 AB 4
例1
思考二:头注运算本质化繁为简
椭圆x+x=1(>b>0离心率为,长轴端点与短轴端点的距离为√5
(1)求椭圆的方程;
4
(2)经过D(,4)的直线与椭圆C交于两点E,F,O为坐标原点,若△OEF为直
角三角形,求直线l的斜率
直线与曲线交点一直线与直线的交点
解:设E(x1,y),F(x2,y2);
①∠EOF=90,x2+yy2=0→k=√19
4k4
②∠OEF=9
OE·y
k→E:
EF: y=kx+4
k2+1k2+
-4k
将E代入椭圆:k2+1+(4)2=1→k=±√5
k2+1
同课章节目录
