北京市海淀区进修学校2012-2013学年高一上学期期中 数学试题
文档属性
| 名称 | 北京市海淀区进修学校2012-2013学年高一上学期期中 数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 147.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-14 16:27:52 | ||
图片预览



文档简介
2012—2013学年度第一学期期中练习
高一数学
考生须 知
1、本试卷共6 页,包 三个大题,20小题,满分为100 分。考试时间120分钟。
2、答题前,考生应认真在密封线外填写班级、姓名和学号
3、请不要用铅笔答题
选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项
是符合要求的,把答案填在答题卡.
1.已知集合,那么 ( )
A. B. C. D.
2.已知函数,那么的值为 ( )
A、 B、
C、 D、
3.已知集合到的映射,那么集合中元素2在中所对应的元素是( )
A.2 B.5 C.6 D.8
4.下列各式错误的是 ( )
A. B.
C. D.
5.在同一坐标系中,函数与的图象之间的关系是( )
A.关于轴对称 B.关于轴对称 C.关于原点对称 D.关于直线对称
6. 下列函数中,满足“对任意,,当时,都有”的是( )
A. B. C. D.
7. 设为常数,函数,若为偶函数,则等于( )
A. B.1 C.2 D.
8.已知函数在内存在一个零点,则实数的取值范围是( )
A. B.
C.或 D
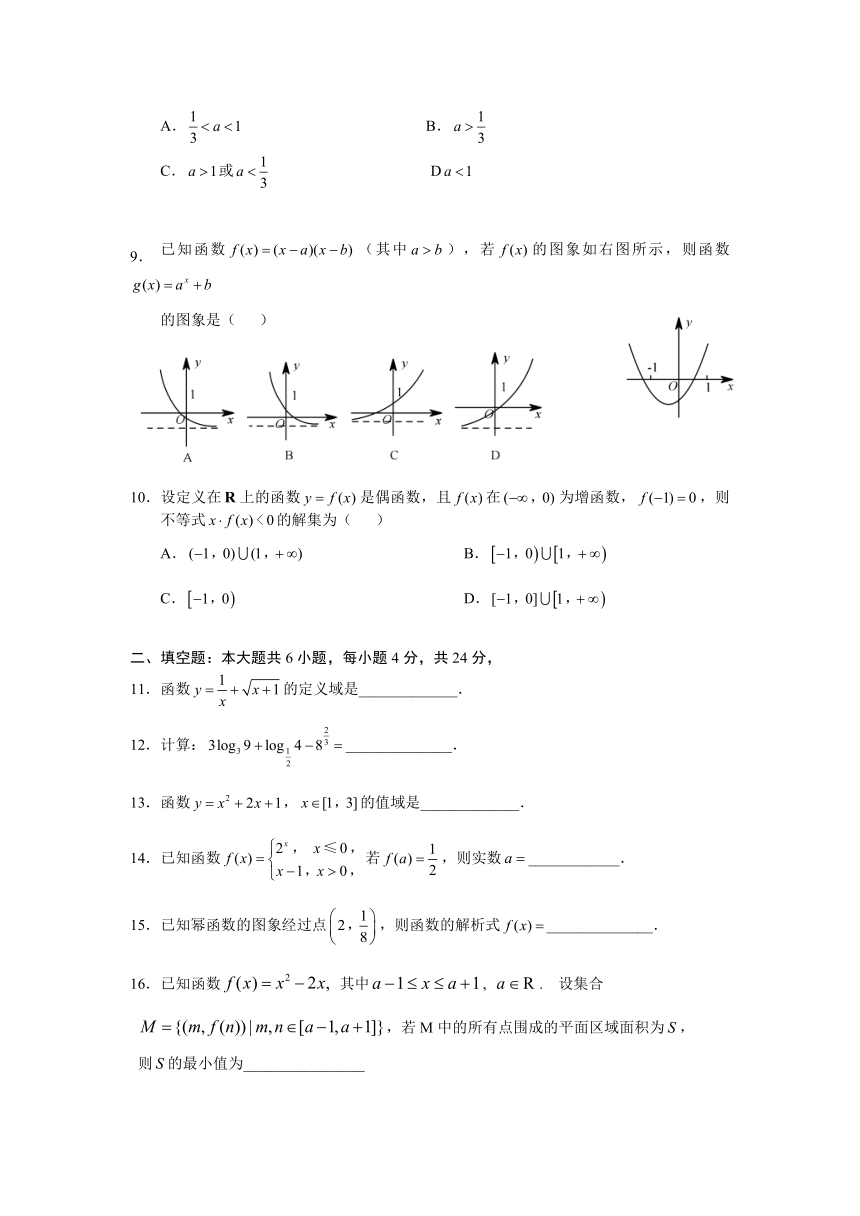
已知函数(其中),若的图象如右图所示,则函数
的图象是( )
10.设定义在上的函数是偶函数,且在为增函数,,则不等式的解集为( )
A. B.
C. D.
二、填空题:本大题共6小题,每小题4分,共24分,
11.函数的定义域是_____________.
12.计算:______________.
13.函数,的值域是_____________.
14.已知函数若,则实数____________.
15.已知幂函数的图象经过点,则函数的解析式______________.
16.已知函数 其中, . 设集合
,若M中的所有点围成的平面区域面积为,
则的最小值为________________
三、解答题:本大题共4小题,共36分,解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分6分)
设集合,,若
(1),求的取值范围.
(2),求的取值范围.
18.(本小题满分10分)
已知.
(I) 求函数的定义域;
(II) 判断函数的奇偶性;
(III)求的值.
19.(本题满分10分)
已知函数.
⑴ 求的值;
⑵ 判断函数在上单调性,并用定义加以证明.
(3)当x取什么值时,的图像在x轴上方?
20.(本小题满分10分)
已知函数且在区间上的最大值是7,求的值
草稿纸
答题纸
一、 选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项
是符合要求的,把答案填在答题卡
题号
1
2
3
4
5
6
7
8
9
10
答案
填空题:本大题共6小题,每小题4分,共24分
; 12. ;
13. ; 14. ;
15. ; 16. ;
三、解答题:本大题共4小题,共36分,解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分6分)
18.(本小题满分10分)
(本题满分10分)
21世纪教育网
20.(本小题满分10分)
2012—2013学年度第一学期期中练习
高一数学 答案
一、选择题 ADBCBBDCAA
二、填空题
11. 12.0 13.[0.15] 14. 15. 16.2
解:(1) ,....................2分
.....................................................................4分21世纪教育网
,......................................6分
18.解: ( I ) 因为 ……………………………….1分
所以, 得到 …………………….2分
所以函数的定义域为 …………………….3分
( II ) 函数的定义域为,
当时, ………… …….4分
因为 …………….5分
…………….6分
所以函数是偶函数 …….7分
( III ) 因为
…………….9分
=
19.解:(1) ................................................2分
(2)函数在上单调递减...........................................3分
证明:设是上的任意两个实数,且,则................4分
....................6分
由,得,且
于是
所以,在上是减函数 .......................... 21世纪教育网........8分
(3) 得........................................................10分
21世纪教育网
20.
解:设,则...............2分
(1)当时,,
此时,在上是增函数................................4分
,(舍)
............................................................................6分
当时,,
此时,在上是增函数
.............8分
,(舍)...................9分
综上所述:.或...........................................................................10分
21世纪教育网
高一数学
考生须 知
1、本试卷共6 页,包 三个大题,20小题,满分为100 分。考试时间120分钟。
2、答题前,考生应认真在密封线外填写班级、姓名和学号
3、请不要用铅笔答题
选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项
是符合要求的,把答案填在答题卡.
1.已知集合,那么 ( )
A. B. C. D.
2.已知函数,那么的值为 ( )
A、 B、
C、 D、
3.已知集合到的映射,那么集合中元素2在中所对应的元素是( )
A.2 B.5 C.6 D.8
4.下列各式错误的是 ( )
A. B.
C. D.
5.在同一坐标系中,函数与的图象之间的关系是( )
A.关于轴对称 B.关于轴对称 C.关于原点对称 D.关于直线对称
6. 下列函数中,满足“对任意,,当时,都有”的是( )
A. B. C. D.
7. 设为常数,函数,若为偶函数,则等于( )
A. B.1 C.2 D.
8.已知函数在内存在一个零点,则实数的取值范围是( )
A. B.
C.或 D
已知函数(其中),若的图象如右图所示,则函数
的图象是( )
10.设定义在上的函数是偶函数,且在为增函数,,则不等式的解集为( )
A. B.
C. D.
二、填空题:本大题共6小题,每小题4分,共24分,
11.函数的定义域是_____________.
12.计算:______________.
13.函数,的值域是_____________.
14.已知函数若,则实数____________.
15.已知幂函数的图象经过点,则函数的解析式______________.
16.已知函数 其中, . 设集合
,若M中的所有点围成的平面区域面积为,
则的最小值为________________
三、解答题:本大题共4小题,共36分,解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分6分)
设集合,,若
(1),求的取值范围.
(2),求的取值范围.
18.(本小题满分10分)
已知.
(I) 求函数的定义域;
(II) 判断函数的奇偶性;
(III)求的值.
19.(本题满分10分)
已知函数.
⑴ 求的值;
⑵ 判断函数在上单调性,并用定义加以证明.
(3)当x取什么值时,的图像在x轴上方?
20.(本小题满分10分)
已知函数且在区间上的最大值是7,求的值
草稿纸
答题纸
一、 选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项
是符合要求的,把答案填在答题卡
题号
1
2
3
4
5
6
7
8
9
10
答案
填空题:本大题共6小题,每小题4分,共24分
; 12. ;
13. ; 14. ;
15. ; 16. ;
三、解答题:本大题共4小题,共36分,解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分6分)
18.(本小题满分10分)
(本题满分10分)
21世纪教育网
20.(本小题满分10分)
2012—2013学年度第一学期期中练习
高一数学 答案
一、选择题 ADBCBBDCAA
二、填空题
11. 12.0 13.[0.15] 14. 15. 16.2
解:(1) ,....................2分
.....................................................................4分21世纪教育网
,......................................6分
18.解: ( I ) 因为 ……………………………….1分
所以, 得到 …………………….2分
所以函数的定义域为 …………………….3分
( II ) 函数的定义域为,
当时, ………… …….4分
因为 …………….5分
…………….6分
所以函数是偶函数 …….7分
( III ) 因为
…………….9分
=
19.解:(1) ................................................2分
(2)函数在上单调递减...........................................3分
证明:设是上的任意两个实数,且,则................4分
....................6分
由,得,且
于是
所以,在上是减函数 .......................... 21世纪教育网........8分
(3) 得........................................................10分
21世纪教育网
20.
解:设,则...............2分
(1)当时,,
此时,在上是增函数................................4分
,(舍)
............................................................................6分
当时,,
此时,在上是增函数
.............8分
,(舍)...................9分
综上所述:.或...........................................................................10分
21世纪教育网
同课章节目录
