2021-2022学年北师大版九年级数学下册第二章二次函数单元测试训练卷(Word版,附答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册第二章二次函数单元测试训练卷(Word版,附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 138.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-27 23:24:41 | ||
图片预览


文档简介
北师大版九年级数学下册
第二章 二次函数
单元测试训练卷
一、选择题(共8小题,4*8=32)
1. 已知抛物线y=(m-1)x2-mx-m2+1的图象过原点,则m的值为( )
A.±1 B.0 C.1 D.-1
2. 在同一平面直角坐标系中,函数y=ax+b与y=ax2-bx的图象可能是( )
A B C D
3. 抛物线y=x2-1可由下列哪一个函数的图象向右平移1个单位,再向下平移2个单位得到?( )
A.y=(x-1)2+1 B.y=(x+1)2+1
C.y=(x-1)2-3 D.y=(x+1)2+3
4. 关于函数y=3x2的性质的叙述,错误的是( )
A.顶点是原点
B.y有最大值
C.当x>0时,y随x的增大而增大
D.当x<0时,y随x的增大而减小
5. 若A,B,C为二次函数y=x2+4x-5的图象上的三点,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y2>y1>y3
C.y3>y1>y2 D.y1>y3>y2
6. 抛物线y=x2+bx+c(其中b,c是常数)过点A(2,6),且抛物线的对称轴与线段y=0(1≤x≤3)有交点,则c的值不可能是( )
A.4 B.6 C.8 D.10
7. 从地面竖直向上抛出一个小球,小球的高度h(m)与小球运动的时间t(s)之间的关系式为h=30t-5t2,那么小球从抛出至回落到地面所需要的时间是( )
A.6 s B.4 s C.3 s D.2 s
8. 抛物线y=ax2+bx+3(a≠0)过A(4,4)、B(2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是( )
A.m≤2或m≥3 B.m≤3或m≥4
C.2<m<3 D.3<m<4
二.填空题(共6小题,4*6=24)
9.若抛物线 y = ax2 + bx + c 的开口向下,则 a 的值可能是________.(写一个即可)
10. 抛物线y=2x2-4x的开口向________,顶点坐标是________.
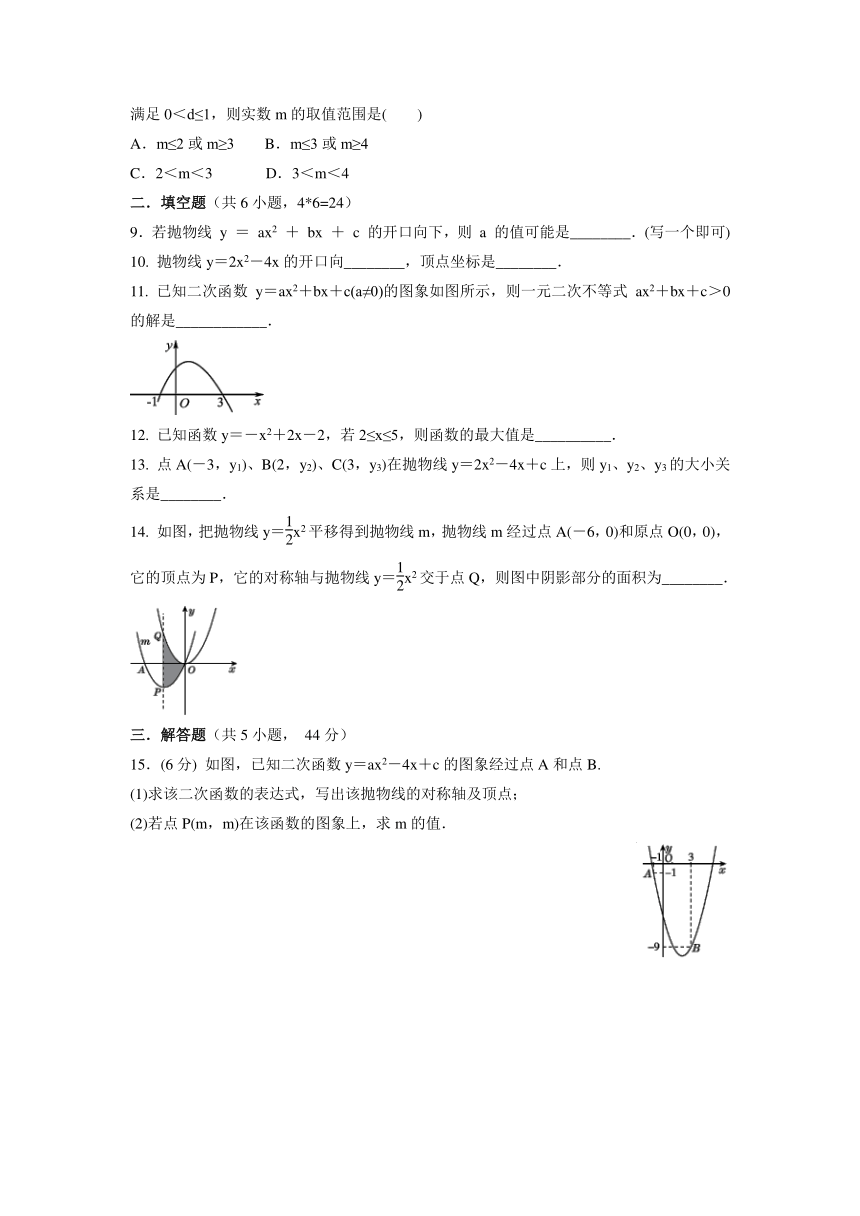
11. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则一元二次不等式ax2+bx+c>0的解是____________.
12. 已知函数y=-x2+2x-2,若2≤x≤5,则函数的最大值是__________.
13. 点A(-3,y1)、B(2,y2)、C(3,y3)在抛物线y=2x2-4x+c上,则y1、y2、y3的大小关系是________.
14. 如图,把抛物线y=x2平移得到抛物线m,抛物线m经过点A(-6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=x2交于点Q,则图中阴影部分的面积为________.
三.解答题(共5小题, 44分)
15.(6分) 如图,已知二次函数y=ax2-4x+c的图象经过点A和点B.
(1)求该二次函数的表达式,写出该抛物线的对称轴及顶点;
(2)若点P(m,m)在该函数的图象上,求m的值.
16.(8分) 如图,二次函数的图象过A,B,C三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.
(1)求二次函数的表达式,并求出函数的最大值;
(2)在抛物线的对称轴上是否存在一点P,使PA+PC最小?若存在,求出点P的坐标;若不存在,请说明理由.
17.(8分) 一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
18.(10分) 如图,有一条双向公路隧道,其截面由抛物线和矩形ABCO组成,隧道最大高度为4.9 m,AB=10 m,BC=2.4 m.现把隧道的截面放在直角坐标系中,若有一辆高为4 m、宽为2 m的装有集装箱的汽车要通过隧道,如果不考虑其他因素,汽车的右侧离隧道的右壁超过多少米才不至于碰到隧道顶部?(抛物线部分为隧道顶部,AO,BC为壁)
19.(12分) 如图①,在平面直角坐标系xOy中,抛物线y=ax2+bx+3经过点A(-1,0),B(3,0)两点,且与y轴交于点C.
(1)求抛物线的表达式;
(2)如图②,用宽为4个单位长度的直尺垂直于x轴,并沿x轴左右平移,直尺的左右两边所在的直线与抛物线相交于P,Q两点(点P在点Q的左侧),连接PQ,在线段PQ上方抛物线上有一动点D,连接DP,DQ.
(1)若点P的横坐标为-,求△DPQ面积的最大值,并求此时点D的坐标;
(2)直尺在平移过程中,△DPQ面积是否有最大值?若有,求出面积的最大值;若没有,请说明理由.
参考答案
1-4DCBB 5-8DAAB
9.-1(答案不唯一,小于零即可)
10.上 (1,-2)
11.-112.-2
13.y2<y3<y1
14.
15.解:(1)将A(-1,-1),B(3,-9)的坐标分别代入y=ax2-4x+c,得解得解得该二次函数的表达式为y=x2-4x-6.∵y=x2-4x-6=(x-2)2-10,∴该抛物线的对称轴为直线x=2,顶点为(2,-10).
(2)∵点P(m,m)在该函数的图象上,∴m2-4m-6=m.∴m1=6,m2=-1.∴m的值为6或-1.
16.解:(1)y=-x2+x+5=-(x-)2+,∴当x=时,y最大值=
(2)存在,∵BC:y=-x+5,当x=时,y=,∴存在P(,)
17.解:(1)y与x的函数关系式为y=-x+40(10≤x≤16)
(2)根据题意知,W=(x-10)y=(x-10)(-x+40)=-x2+50x-400=-(x-25)2+225,∵a=-1<0,∴当x<25时,W随x的增大而增大,∵10≤x≤16,∴当x=16时,W取得最大值,最大值为144
18.解:如图所示.
由题意得抛物线的顶点坐标为(5,2.5),且过点O(0,0)和点C(10,0),可求出抛物线的函数表达式为y=-x2+x.用矩形DEFG表示汽车的截面,设BD=m,延长DG交抛物线于H,且DG交x轴于M,则AD=10-m,HM=-(10-m)2+10-m.∴HD=-(10-m)2+10-m+2.4.由题意得-(10-m)2+12.4-m>4,化简得(m-2)(m-8)<0,∴2<m<8.答:汽车的右侧离隧道右壁超过2 m才不至于碰到隧道顶部.
19.解:(1)y=-x2+2x+3 (2)(Ⅰ)当点P的横坐标为-时,点Q的横坐标为,∴此时点P的坐标为(-,),点Q的坐标为(,-).易求直线PQ的表达式为y=-x+.
如图,过点D作DE∥y轴交直线PQ于点E,设点D的坐标为(x,-x2+2x+3),则点E的坐标为(x,-x+),∴DE=-x2+2x+3-(-x+)=-x2+3x+,∴S△DPQ=DE·(xQ-xP)=-2x2+6x+=-2(x-)2+8.∵-2<0,∴当x=时,△DPQ的面积取最大值,最大值为8,此时点D的坐标为(,)
(2)假设存在,设点P的横坐标为t,则点Q的横坐标为4+t,∴点P的坐标为(t,-t2+2t+3),点Q的坐标为[4+t,-(4+t)2+2(4+t)+3],利用待定系数法易知,直线PQ的表达式为y=-2(t+1)x+t2+4t+3.设点D的坐标为(x,-x2+2x+3),则点E的坐标为(x,-2(t+1)x+t2+4t+3),∴DE=-x2+2x+3-[-2(t+1)x+t2+4t+3]=-x2+2(t+2)x-t2-4t,∴S△DPQ=DE·(xQ-xP)=-2x2+4(t+2)x-2t2-8t=-2[x-(t+2)]2+8.∵-2<0,∴当x=t+2时,△DPQ的面积有最大值,最大值为8
第二章 二次函数
单元测试训练卷
一、选择题(共8小题,4*8=32)
1. 已知抛物线y=(m-1)x2-mx-m2+1的图象过原点,则m的值为( )
A.±1 B.0 C.1 D.-1
2. 在同一平面直角坐标系中,函数y=ax+b与y=ax2-bx的图象可能是( )
A B C D
3. 抛物线y=x2-1可由下列哪一个函数的图象向右平移1个单位,再向下平移2个单位得到?( )
A.y=(x-1)2+1 B.y=(x+1)2+1
C.y=(x-1)2-3 D.y=(x+1)2+3
4. 关于函数y=3x2的性质的叙述,错误的是( )
A.顶点是原点
B.y有最大值
C.当x>0时,y随x的增大而增大
D.当x<0时,y随x的增大而减小
5. 若A,B,C为二次函数y=x2+4x-5的图象上的三点,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y2>y1>y3
C.y3>y1>y2 D.y1>y3>y2
6. 抛物线y=x2+bx+c(其中b,c是常数)过点A(2,6),且抛物线的对称轴与线段y=0(1≤x≤3)有交点,则c的值不可能是( )
A.4 B.6 C.8 D.10
7. 从地面竖直向上抛出一个小球,小球的高度h(m)与小球运动的时间t(s)之间的关系式为h=30t-5t2,那么小球从抛出至回落到地面所需要的时间是( )
A.6 s B.4 s C.3 s D.2 s
8. 抛物线y=ax2+bx+3(a≠0)过A(4,4)、B(2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是( )
A.m≤2或m≥3 B.m≤3或m≥4
C.2<m<3 D.3<m<4
二.填空题(共6小题,4*6=24)
9.若抛物线 y = ax2 + bx + c 的开口向下,则 a 的值可能是________.(写一个即可)
10. 抛物线y=2x2-4x的开口向________,顶点坐标是________.
11. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则一元二次不等式ax2+bx+c>0的解是____________.
12. 已知函数y=-x2+2x-2,若2≤x≤5,则函数的最大值是__________.
13. 点A(-3,y1)、B(2,y2)、C(3,y3)在抛物线y=2x2-4x+c上,则y1、y2、y3的大小关系是________.
14. 如图,把抛物线y=x2平移得到抛物线m,抛物线m经过点A(-6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=x2交于点Q,则图中阴影部分的面积为________.
三.解答题(共5小题, 44分)
15.(6分) 如图,已知二次函数y=ax2-4x+c的图象经过点A和点B.
(1)求该二次函数的表达式,写出该抛物线的对称轴及顶点;
(2)若点P(m,m)在该函数的图象上,求m的值.
16.(8分) 如图,二次函数的图象过A,B,C三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.
(1)求二次函数的表达式,并求出函数的最大值;
(2)在抛物线的对称轴上是否存在一点P,使PA+PC最小?若存在,求出点P的坐标;若不存在,请说明理由.
17.(8分) 一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
18.(10分) 如图,有一条双向公路隧道,其截面由抛物线和矩形ABCO组成,隧道最大高度为4.9 m,AB=10 m,BC=2.4 m.现把隧道的截面放在直角坐标系中,若有一辆高为4 m、宽为2 m的装有集装箱的汽车要通过隧道,如果不考虑其他因素,汽车的右侧离隧道的右壁超过多少米才不至于碰到隧道顶部?(抛物线部分为隧道顶部,AO,BC为壁)
19.(12分) 如图①,在平面直角坐标系xOy中,抛物线y=ax2+bx+3经过点A(-1,0),B(3,0)两点,且与y轴交于点C.
(1)求抛物线的表达式;
(2)如图②,用宽为4个单位长度的直尺垂直于x轴,并沿x轴左右平移,直尺的左右两边所在的直线与抛物线相交于P,Q两点(点P在点Q的左侧),连接PQ,在线段PQ上方抛物线上有一动点D,连接DP,DQ.
(1)若点P的横坐标为-,求△DPQ面积的最大值,并求此时点D的坐标;
(2)直尺在平移过程中,△DPQ面积是否有最大值?若有,求出面积的最大值;若没有,请说明理由.
参考答案
1-4DCBB 5-8DAAB
9.-1(答案不唯一,小于零即可)
10.上 (1,-2)
11.-1
13.y2<y3<y1
14.
15.解:(1)将A(-1,-1),B(3,-9)的坐标分别代入y=ax2-4x+c,得解得解得该二次函数的表达式为y=x2-4x-6.∵y=x2-4x-6=(x-2)2-10,∴该抛物线的对称轴为直线x=2,顶点为(2,-10).
(2)∵点P(m,m)在该函数的图象上,∴m2-4m-6=m.∴m1=6,m2=-1.∴m的值为6或-1.
16.解:(1)y=-x2+x+5=-(x-)2+,∴当x=时,y最大值=
(2)存在,∵BC:y=-x+5,当x=时,y=,∴存在P(,)
17.解:(1)y与x的函数关系式为y=-x+40(10≤x≤16)
(2)根据题意知,W=(x-10)y=(x-10)(-x+40)=-x2+50x-400=-(x-25)2+225,∵a=-1<0,∴当x<25时,W随x的增大而增大,∵10≤x≤16,∴当x=16时,W取得最大值,最大值为144
18.解:如图所示.
由题意得抛物线的顶点坐标为(5,2.5),且过点O(0,0)和点C(10,0),可求出抛物线的函数表达式为y=-x2+x.用矩形DEFG表示汽车的截面,设BD=m,延长DG交抛物线于H,且DG交x轴于M,则AD=10-m,HM=-(10-m)2+10-m.∴HD=-(10-m)2+10-m+2.4.由题意得-(10-m)2+12.4-m>4,化简得(m-2)(m-8)<0,∴2<m<8.答:汽车的右侧离隧道右壁超过2 m才不至于碰到隧道顶部.
19.解:(1)y=-x2+2x+3 (2)(Ⅰ)当点P的横坐标为-时,点Q的横坐标为,∴此时点P的坐标为(-,),点Q的坐标为(,-).易求直线PQ的表达式为y=-x+.
如图,过点D作DE∥y轴交直线PQ于点E,设点D的坐标为(x,-x2+2x+3),则点E的坐标为(x,-x+),∴DE=-x2+2x+3-(-x+)=-x2+3x+,∴S△DPQ=DE·(xQ-xP)=-2x2+6x+=-2(x-)2+8.∵-2<0,∴当x=时,△DPQ的面积取最大值,最大值为8,此时点D的坐标为(,)
(2)假设存在,设点P的横坐标为t,则点Q的横坐标为4+t,∴点P的坐标为(t,-t2+2t+3),点Q的坐标为[4+t,-(4+t)2+2(4+t)+3],利用待定系数法易知,直线PQ的表达式为y=-2(t+1)x+t2+4t+3.设点D的坐标为(x,-x2+2x+3),则点E的坐标为(x,-2(t+1)x+t2+4t+3),∴DE=-x2+2x+3-[-2(t+1)x+t2+4t+3]=-x2+2(t+2)x-t2-4t,∴S△DPQ=DE·(xQ-xP)=-2x2+4(t+2)x-2t2-8t=-2[x-(t+2)]2+8.∵-2<0,∴当x=t+2时,△DPQ的面积有最大值,最大值为8
