2022届高三数学二轮复习圆锥曲线热点问题 课件(32张ppt)
文档属性
| 名称 | 2022届高三数学二轮复习圆锥曲线热点问题 课件(32张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-29 12:03:32 | ||
图片预览









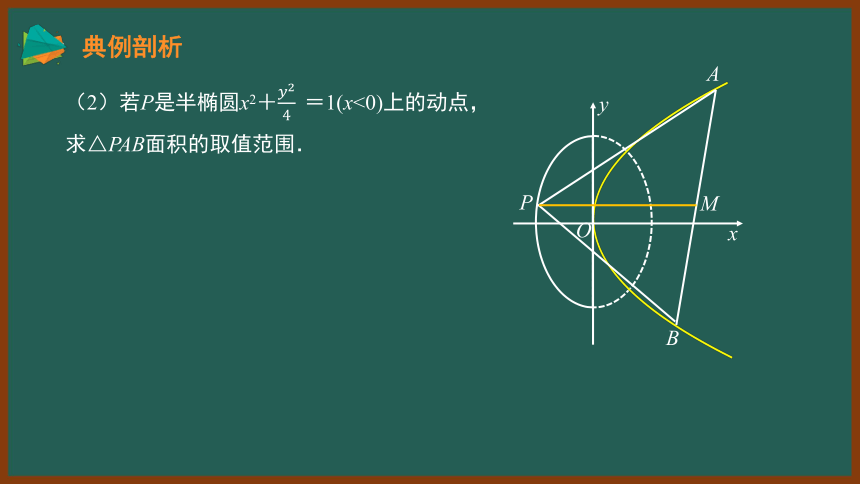


文档简介
(共32张PPT)
高三二轮复习
《圆锥曲线热点问题》
热点1:最值问题
【例1】已知椭圆E:(a>b>0)的左右焦点为F1,F2,离心率为,过点F2且垂直于 x轴的直线被椭圆E截得的弦长为1.
(1)求椭圆E的方程;
(2)若直线 y=kx+m(k>0)交椭圆E于点C,D两点,与线段F1F2和椭圆短轴分别交于两个不同点M,N,且|CM|=|DN|,求|CD|的最小值.
【例1】已知椭圆E:(a>b>0)的左右焦点为F1,F2,离心率为,过点F2且垂直于 x轴的直线被椭圆E截得的弦长为1.
(1)求椭圆E的方程;
O
x
y
F1
F2
(2)若直线 y=kx+m(k>0)交椭圆E于点C,D两点,与线段F1F2和椭圆短轴分别交于两个不同点M,N,且|CM|=|DN|,求|CD|的最小值.
O
x
y
F1
F2
C
D
M
N
最值问题的求解思路
根据目标函数的特征选择相应的方法进行求解.
建立目标函数
利用已知或隐含的不等关系,构建以待求量为元的不等式求解,且大多会用到基本不等式.
构建不等式
热点2:范围问题
【例2】如图,已知点P是 y轴左侧(不含y轴)一点,抛物线C:y2=4x上存在不同的两点A,B满足PA,PB的中点均在C上.
(1)设AB中点为M,证明:PM垂直于y轴;
(2)若P是半椭圆x2+=1(x<0)上的动点,求△PAB面积的取值范围.
O
x
y
B
P
A
M
【例2】如图,已知点P是 y轴左侧(不含y轴)一点,抛物线C:y2=4x上存在不同的两点A,B满足PA,PB的中点均在C上.
(1)设AB中点为M,证明:PM垂直于y轴;
O
x
y
B
P
A
M
(2)若P是半椭圆x2+=1(x<0)上的动点,求△PAB面积的取值范围.
O
x
y
B
P
A
M
圆锥曲线中的取值范围问题的5种常用解法
利用圆锥曲线的几何性质或判别式构造不等关系,从而确定参数的取值范围.
利用已知参数的范围,求新参数的范围,解这类问题的核心是建立两个参数之间的等量关系.
利用隐含的不等关系建立不等式,从而求出参数的取值范围.
利用已知的不等关系构造不等式,从而求出参数的取值范围.
利用求函数的值域的方法将待求量表示为其他变量的函数,求其值域,从而确定参数的取值范围.
热点3:证明问题
【例3】在平面直角坐标系xOy中,已知向量=(x+,y), =(x ,y),且||+||=4.
(1)求动点P(x,y)的轨迹C的方程;
(2)已知直线 l过坐标原点,且与(1)中的轨迹C交于M,N两点,M在第三象限,且MH⊥x轴,垂足为H,连接NH并延长交C于点Q,证明:QM⊥MN.
【例3】在平面直角坐标系xOy中,已知向量=(x+,y), =(x ,y),且||+||=4.
(1)求动点P(x,y)的轨迹C的方程;
(2)已知直线 l过坐标原点,且与(1)中的轨迹C交于M,N两点,M在第三象限,且MH⊥x轴,垂足为H,连接NH并延长交C于点Q,证明:QM⊥MN.
O
x
y
M
N
H
Q
圆锥曲线中的证明问题
圆锥曲线中的证明问题主要有两类:一是证明点、直线、曲线等几何元素中的位置关系,如某点在某直线上,某直线经过某个点,某两条直线平行或垂直;二是证明直线与圆锥曲线中的一些数量关系(相等或者不等).
在证明问题时,主要依据直线和圆锥曲线的性质、直线与圆锥曲线的位置关系等,把几何条件恰当地转化为代数式子,通过相关性质的应用、代数式的恒等变形以及必要的数值计算进行证明.
热点4:定点问题
【例4】已知椭圆E: (a>b>0)的离心率e=,且点P()为椭圆E上一点.点A,B为椭圆E的上下顶点,动点M在第一象限内且坐标为(m,2),过M作直线MA,MB分别交椭圆E于C,D两点.
(1)求椭圆E的标准方程;
(2)问直线CD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
【例4】已知椭圆E: (a>b>0)的离心率e=,且点P()为椭圆E上一点.点A,B为椭圆E的上下顶点,动点M在第一象限内且坐标为(m,2),过M作直线MA,MB分别交椭圆E于C,D两点.
(1)求椭圆E的标准方程;
(2)问直线CD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
O
x
y
A
B
M(m,2)
C
D
动线过定点问题的两大类型及解法
动直线l过定点问题
解法:设动直线方程(斜率存在)为y=kx+t,由题设条件将t用k表示为t=m(k),得y=k(x+m),故动直线过定点(-m,0).
动曲线C过定点问题
解法:引入参变量建立曲线C的方程,再根据其对参变量恒成立,令其系数等于零,得出定点.
热点5:定值问题
【例5】已知椭圆C的对称中心为原点O,焦点在x轴上,焦距为,点(2,1)在该椭圆上.
(1)求椭圆C的方程;
(2)直线 x=2与椭圆交于P,Q两点,P点位于第一象限,A,B是椭圆上位于直线x=2两侧的动点.当点A,B运动时,满足∠APQ=∠BPQ,问直线AB的斜率是否为定值,请说明理由.
【例5】已知椭圆C的对称中心为原点O,焦点在x轴上,焦距为,点(2,1)在该椭圆上.
(1)求椭圆C的方程;
(2)直线 x=2与椭圆交于P,Q两点,P点位于第一象限,A,B是椭圆上位于直线x=2两侧的动点.当点A,B运动时,满足∠APQ=∠BPQ,问直线AB的斜率是否为定值,请说明理由.
O
x
y
2
P
Q
A
B
求定值问题常见的两种方法
直接推理、计算,并在计算推理的过程中消去变量,从而得到定值.
从特殊入手,求出定值,再证明这个值与变量无关.
热点6:存在性问题
【例6】已知椭圆C: (a>b>0)的两个焦点分别为F1,F2,且F1是圆x2+y2 x+7=0的圆心,点H的坐标为(0,b),且△HF1F2的面积为.
(1)求椭圆C的方程;
(2)是否存在直线 y=2x+t 与椭圆C相交于M,N两点,使得直线HM与HN的斜率之和为1?若存在,求此时的直线方程;若不存在,请说明理由.
【例6】已知椭圆C: (a>b>0)的两个焦点分别为F1,F2,且F1是圆
x2+y2 x+7=0的圆心,点H的坐标为(0,b),且△HF1F2的面积为.
(1)求椭圆C的方程;
O
x
y
F1
F2
H
(2)是否存在直线 y=2x+t 与椭圆C相交于M,N两点,使得直线HM与HN的斜率之和为1?若存在,求此时的直线方程;若不存在,请说明理由.
O
x
y
H
M
N
求解存在性问题的思路及策略
思路
策略
①当条件和结论不唯一时要分类讨论;
②当给出结论而要推导出存在的条件时,先假设成立,再推出条件.
先假设存在,推证满足条件的结论,若结论正确,则存在;若结论不正确,则不存在.
再见!
高三二轮复习
《圆锥曲线热点问题》
热点1:最值问题
【例1】已知椭圆E:(a>b>0)的左右焦点为F1,F2,离心率为,过点F2且垂直于 x轴的直线被椭圆E截得的弦长为1.
(1)求椭圆E的方程;
(2)若直线 y=kx+m(k>0)交椭圆E于点C,D两点,与线段F1F2和椭圆短轴分别交于两个不同点M,N,且|CM|=|DN|,求|CD|的最小值.
【例1】已知椭圆E:(a>b>0)的左右焦点为F1,F2,离心率为,过点F2且垂直于 x轴的直线被椭圆E截得的弦长为1.
(1)求椭圆E的方程;
O
x
y
F1
F2
(2)若直线 y=kx+m(k>0)交椭圆E于点C,D两点,与线段F1F2和椭圆短轴分别交于两个不同点M,N,且|CM|=|DN|,求|CD|的最小值.
O
x
y
F1
F2
C
D
M
N
最值问题的求解思路
根据目标函数的特征选择相应的方法进行求解.
建立目标函数
利用已知或隐含的不等关系,构建以待求量为元的不等式求解,且大多会用到基本不等式.
构建不等式
热点2:范围问题
【例2】如图,已知点P是 y轴左侧(不含y轴)一点,抛物线C:y2=4x上存在不同的两点A,B满足PA,PB的中点均在C上.
(1)设AB中点为M,证明:PM垂直于y轴;
(2)若P是半椭圆x2+=1(x<0)上的动点,求△PAB面积的取值范围.
O
x
y
B
P
A
M
【例2】如图,已知点P是 y轴左侧(不含y轴)一点,抛物线C:y2=4x上存在不同的两点A,B满足PA,PB的中点均在C上.
(1)设AB中点为M,证明:PM垂直于y轴;
O
x
y
B
P
A
M
(2)若P是半椭圆x2+=1(x<0)上的动点,求△PAB面积的取值范围.
O
x
y
B
P
A
M
圆锥曲线中的取值范围问题的5种常用解法
利用圆锥曲线的几何性质或判别式构造不等关系,从而确定参数的取值范围.
利用已知参数的范围,求新参数的范围,解这类问题的核心是建立两个参数之间的等量关系.
利用隐含的不等关系建立不等式,从而求出参数的取值范围.
利用已知的不等关系构造不等式,从而求出参数的取值范围.
利用求函数的值域的方法将待求量表示为其他变量的函数,求其值域,从而确定参数的取值范围.
热点3:证明问题
【例3】在平面直角坐标系xOy中,已知向量=(x+,y), =(x ,y),且||+||=4.
(1)求动点P(x,y)的轨迹C的方程;
(2)已知直线 l过坐标原点,且与(1)中的轨迹C交于M,N两点,M在第三象限,且MH⊥x轴,垂足为H,连接NH并延长交C于点Q,证明:QM⊥MN.
【例3】在平面直角坐标系xOy中,已知向量=(x+,y), =(x ,y),且||+||=4.
(1)求动点P(x,y)的轨迹C的方程;
(2)已知直线 l过坐标原点,且与(1)中的轨迹C交于M,N两点,M在第三象限,且MH⊥x轴,垂足为H,连接NH并延长交C于点Q,证明:QM⊥MN.
O
x
y
M
N
H
Q
圆锥曲线中的证明问题
圆锥曲线中的证明问题主要有两类:一是证明点、直线、曲线等几何元素中的位置关系,如某点在某直线上,某直线经过某个点,某两条直线平行或垂直;二是证明直线与圆锥曲线中的一些数量关系(相等或者不等).
在证明问题时,主要依据直线和圆锥曲线的性质、直线与圆锥曲线的位置关系等,把几何条件恰当地转化为代数式子,通过相关性质的应用、代数式的恒等变形以及必要的数值计算进行证明.
热点4:定点问题
【例4】已知椭圆E: (a>b>0)的离心率e=,且点P()为椭圆E上一点.点A,B为椭圆E的上下顶点,动点M在第一象限内且坐标为(m,2),过M作直线MA,MB分别交椭圆E于C,D两点.
(1)求椭圆E的标准方程;
(2)问直线CD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
【例4】已知椭圆E: (a>b>0)的离心率e=,且点P()为椭圆E上一点.点A,B为椭圆E的上下顶点,动点M在第一象限内且坐标为(m,2),过M作直线MA,MB分别交椭圆E于C,D两点.
(1)求椭圆E的标准方程;
(2)问直线CD是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.
O
x
y
A
B
M(m,2)
C
D
动线过定点问题的两大类型及解法
动直线l过定点问题
解法:设动直线方程(斜率存在)为y=kx+t,由题设条件将t用k表示为t=m(k),得y=k(x+m),故动直线过定点(-m,0).
动曲线C过定点问题
解法:引入参变量建立曲线C的方程,再根据其对参变量恒成立,令其系数等于零,得出定点.
热点5:定值问题
【例5】已知椭圆C的对称中心为原点O,焦点在x轴上,焦距为,点(2,1)在该椭圆上.
(1)求椭圆C的方程;
(2)直线 x=2与椭圆交于P,Q两点,P点位于第一象限,A,B是椭圆上位于直线x=2两侧的动点.当点A,B运动时,满足∠APQ=∠BPQ,问直线AB的斜率是否为定值,请说明理由.
【例5】已知椭圆C的对称中心为原点O,焦点在x轴上,焦距为,点(2,1)在该椭圆上.
(1)求椭圆C的方程;
(2)直线 x=2与椭圆交于P,Q两点,P点位于第一象限,A,B是椭圆上位于直线x=2两侧的动点.当点A,B运动时,满足∠APQ=∠BPQ,问直线AB的斜率是否为定值,请说明理由.
O
x
y
2
P
Q
A
B
求定值问题常见的两种方法
直接推理、计算,并在计算推理的过程中消去变量,从而得到定值.
从特殊入手,求出定值,再证明这个值与变量无关.
热点6:存在性问题
【例6】已知椭圆C: (a>b>0)的两个焦点分别为F1,F2,且F1是圆x2+y2 x+7=0的圆心,点H的坐标为(0,b),且△HF1F2的面积为.
(1)求椭圆C的方程;
(2)是否存在直线 y=2x+t 与椭圆C相交于M,N两点,使得直线HM与HN的斜率之和为1?若存在,求此时的直线方程;若不存在,请说明理由.
【例6】已知椭圆C: (a>b>0)的两个焦点分别为F1,F2,且F1是圆
x2+y2 x+7=0的圆心,点H的坐标为(0,b),且△HF1F2的面积为.
(1)求椭圆C的方程;
O
x
y
F1
F2
H
(2)是否存在直线 y=2x+t 与椭圆C相交于M,N两点,使得直线HM与HN的斜率之和为1?若存在,求此时的直线方程;若不存在,请说明理由.
O
x
y
H
M
N
求解存在性问题的思路及策略
思路
策略
①当条件和结论不唯一时要分类讨论;
②当给出结论而要推导出存在的条件时,先假设成立,再推出条件.
先假设存在,推证满足条件的结论,若结论正确,则存在;若结论不正确,则不存在.
再见!
同课章节目录
