2022届高三数学二轮复习统计 课件(24张ppt)
文档属性
| 名称 | 2022届高三数学二轮复习统计 课件(24张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-29 12:04:50 | ||
图片预览







文档简介
(共24张PPT)
高三二轮复习
——《统计》
小题:抽样方法、样本的数字特征、统计图表的应用等,难度较小;
大题:独立性检验以及回归分析,难度中等.
考点1:用样本估计总体
【例1】如图所示,一家面包销售店根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,图中小矩形从左向右所对应的区间依次为[0,50),[50,100),[100,150),[150,200),[200,250].若一个月以30天计算,估计这家面包店一个月内这种面包的日销售量少于100个的天数为________天.
日销售量/个
频率
组距
0.006
0.005
0.004
0.003
0.002
O
50 100 150 200 250
12
各小矩形的面积表示相应各组的频率,各小矩形的高=频率/组距;
各小矩形面积之和等于1;
中位数左右两侧的直方图面积相等,为平分频率分布直方图面积且垂直于横轴的直线与横轴交点的横坐标;
众数是最高矩形中点的横坐标;
频率分布直方图中均值等于组中值与对应概率乘积的和.
x
频率
组距
O
考点2:统计图表的应用
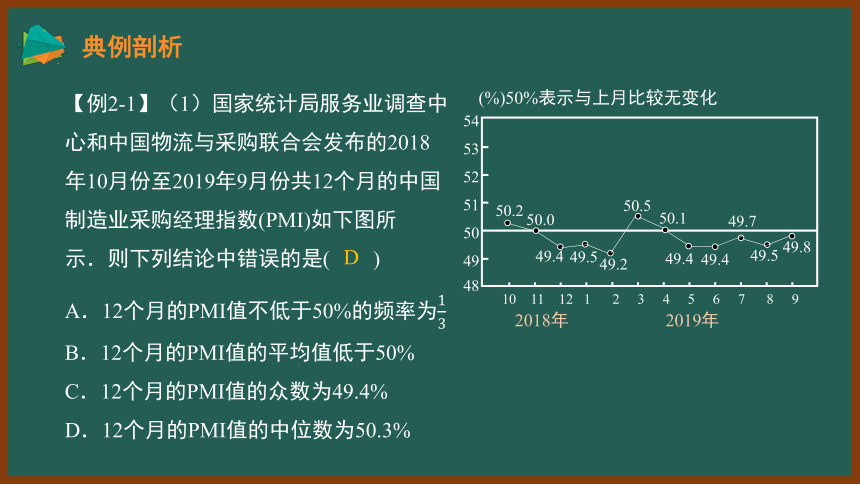
【例2-1】(1)国家统计局服务业调查中心和中国物流与采购联合会发布的2018年10月份至2019年9月份共12个月的中国制造业采购经理指数(PMI)如下图所示.则下列结论中错误的是( )
A.12个月的PMI值不低于50%的频率为
B.12个月的PMI值的平均值低于50%
C.12个月的PMI值的众数为49.4%
D.12个月的PMI值的中位数为50.3%
D
(%)50%表示与上月比较无变化
10 11 12 1 2 3 4 5 6 7 8 9
54
53
52
51
50
48
49
50.2
50.0
49.4
49.5
49.2
50.5
50.1
49.4
49.4
49.7
49.5
49.8
2018年
2019年
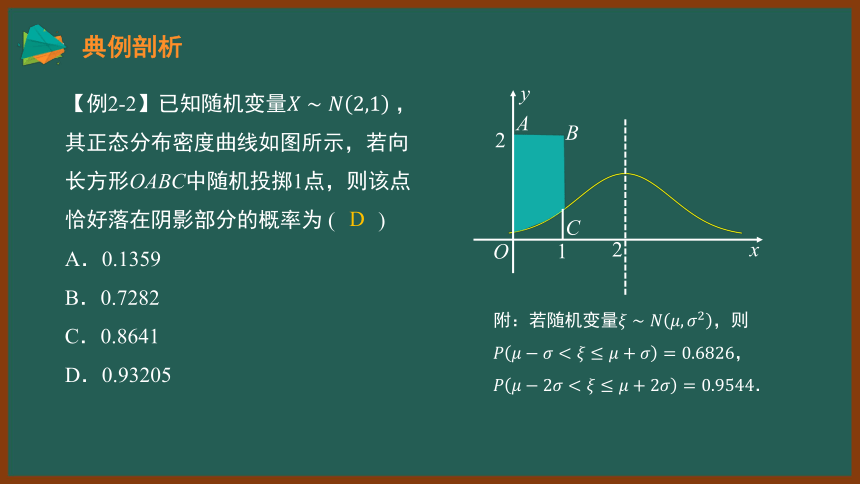
【例2-2】已知随机变量 ,其正态分布密度曲线如图所示,若向长方形OABC中随机投掷1点,则该点恰好落在阴影部分的概率为 ( )
A.0.1359
B.0.7282
C.0.8641
D.0.93205
D
附:若随机变量,则
,
.
y
x
2
O
2
B
C
1
A
【例2-3】某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃.下面叙述不正确的是( )
D
A.各月的平均最低气温都在0℃以上
B.七月的平均温差比一月的平均温差大
C.三月和十一月的平均最高气温基本相同
D.平均最高气温高于20℃的月份有5个
一月
二月
三月
四月
五月
六月
七月
八月
九月
十月
十一月
十二月
A
B
20℃
15℃
10℃
5℃
0℃
平均最低气温
平均最高气温
考点3:回归分析
【例3 1】广告投入对商品的销售额有较大影响,某电商对连续5个年度的广告费 x 和销售额 y 进行统计,得到统计数据如下表(单位:万元)
广告费 2 3 4 5 6
销售额 29 41 50 59 71
由上表可得回归方程为 ,据此模型, 预测广告费为10万元时销售额约为( )
A.118.2万元
B.111.2万元
C.108.8万元
D.101.2万元
B
【例3-2】 随着我国中医学的发展,药用昆虫的使用相应愈来愈多.每年春暖以后至寒冬前,是昆虫大量活动与繁殖季节,易于采集各种药用昆虫.已知一只药用昆虫的产卵数y与一定范围内的温度x有关,于是科研人员在3月份的31天中随机挑选了5天进行研究,现收集了该种药用昆虫的5组观测数据如下表:
日期 2日 7日 15日 22日 30日
温度 10 11 13 12 8
产卵数/个 23 25 30 26 16
(1)从这5天中任选2天,记这两天药用昆虫的产卵分别为m,n,求事件“m,n均不小于25”的概率;
日期 2日 7日 15日 22日 30日
温度 10 11 13 12 8
产卵数/个 23 25 30 26 16
(2)科研人员确定的研究方案是:先从这五组数据中任选2组,用剩下的3组数据建立y关于x的线性回归方程,再对被选取的2组数据进行检验.
(ⅰ)若选取的是3月2日与30日的两组数据,请根据3月7日、15日和22日这三天的数据,求出y关于x的线性回归方程;
(ⅱ)若由线性回归方程得到的估计数据与选出的检验数据的误差均不超过2个,则认为得到的线性回归方程是可靠的,试问(ⅰ)中所得的线性回归方程是否可靠?
附:回归直线的斜率和截距的最小二乘估计公式分别为
回归直线过样本点中心 .
2
可以利用回归直线方程预报在x取某个值时y的估计值.
3
1
求回归直线方程的一般步骤:
依据样本数据画出散点图,确定两个变量具有线性相关关系
计算 的值;
计算回归系数;
写出回归直线方程为.
【例4-1】下列四个命题:①在回归模型中,预报变量 y的值不能由解释变量 x唯一确定;②若变量x,y满足关系y=-0.1x+1,且变量y与z正相关,则x与z也正相关;③在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;④以模型 y=cekx 去拟合一组数据时,为了求出回归方程,设z=lny,将其变换后得到线性方程z=0.3x+4,则c=e4,k=0.3.
其中真命题的个数为( )
A.1个 B.2个 C.3个 D.4个
C
【例4-2】已知某种细菌的适宜生长温度为12℃~27℃,为了研究该种细菌的繁殖数量y(单位:个)随温度 (单位:℃)变化的规律,收集数据如下:
温度 /℃ 14 16 18 20 22 24 26
繁殖数量 /个 25 30 38 50 66 120 218
对数据进行初步处理后,得到了一些统计量的值,如表所示:
20 78 4.1 112 3.8 1590 20.5
其中,
(1)请绘出 y 关于x 的散点图,并根据散点图判断 y=bx+a与y=cedx 哪一个更适合作为该种细菌的繁殖数量y 关于温度 x的回归方程类型(给出判断即可,不必说明理由);
14 16 18 20 22 24 26 x/℃
220
200
180
160
140
120
100
80
60
40
20
O
y/个
(2)根据(1)的判断结果及表格数据,建立 y 关于 x 的回归方程(结果精确到0.1);
(3)当温度为27℃时,该种细菌的繁殖数量的预报值为多少?
参考公式:对于一组数据(i=1,2,3,…,n)其回归直线的斜率和截距的最小二乘估计
分别为 ,参考数据: .
考点4:独立性检验
【例5】某社会机构为了调查对手机游戏的兴趣与年龄的关系,通过问卷调查,整理数据得如下2×2列联表:
40岁以下 40岁以上 合计
很有兴趣 30 15 45
无兴趣 20 35 55
合计 50 50 100
(1)根据列联表,能否有99.9%的把握认为对手机游戏的兴趣程度与年龄有关
(2)若已经从40岁以下的被调查者中用分层抽样的方式抽取了5名,现从这5名被调查者中随机选取3名,求这3名被调查 者中恰有1名对手机游戏无兴趣的概率.
参考公式及数据: ,其中n=a+b+c+d.
P(k2≥k0) 0.05 0.010 0.001
k0 3.841 6.635 10.828
独立性检验的关键
根据2×2列联表准确计算K2,若2×2列联表没有列出来,要先列出此表.
01
K2的观测值k越大,对应假设事件H0成立(两类变量相互独立)的概率越小,H0不成立的概率越大.
02
1.用样本估计总体是统计的基本思想.
2.(1)众数、中位数及平均数都是描述一组数据集中趋势的量,平均数是最重要的量,与每个样本数据有关,这是中位数、众数所不具有的性质.
(2)标准差、方差描述了一组数据围绕平均数波动的大小.标准差、方差越大,数据的离散程度就越大.
3.频率分布表和频率分布直方图都可直观描述样本数据的分布规律.
在频率分布直方图中,可分析样本数据的分布情况,大致判断平均数的范围,并利用数据的波动性大小反映方差(标准差)的大小.
4.回归分析是对具有相关关系的两个变量进行统计分析的方法,只有在散点图大致呈线性时,求出的线性回归方程才有实际意义,否则,求出的线性回归方程毫无意义.根据回归方程进行预报,仅是一个预报值,而不是真实发生的值.
再见!
高三二轮复习
——《统计》
小题:抽样方法、样本的数字特征、统计图表的应用等,难度较小;
大题:独立性检验以及回归分析,难度中等.
考点1:用样本估计总体
【例1】如图所示,一家面包销售店根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,图中小矩形从左向右所对应的区间依次为[0,50),[50,100),[100,150),[150,200),[200,250].若一个月以30天计算,估计这家面包店一个月内这种面包的日销售量少于100个的天数为________天.
日销售量/个
频率
组距
0.006
0.005
0.004
0.003
0.002
O
50 100 150 200 250
12
各小矩形的面积表示相应各组的频率,各小矩形的高=频率/组距;
各小矩形面积之和等于1;
中位数左右两侧的直方图面积相等,为平分频率分布直方图面积且垂直于横轴的直线与横轴交点的横坐标;
众数是最高矩形中点的横坐标;
频率分布直方图中均值等于组中值与对应概率乘积的和.
x
频率
组距
O
考点2:统计图表的应用
【例2-1】(1)国家统计局服务业调查中心和中国物流与采购联合会发布的2018年10月份至2019年9月份共12个月的中国制造业采购经理指数(PMI)如下图所示.则下列结论中错误的是( )
A.12个月的PMI值不低于50%的频率为
B.12个月的PMI值的平均值低于50%
C.12个月的PMI值的众数为49.4%
D.12个月的PMI值的中位数为50.3%
D
(%)50%表示与上月比较无变化
10 11 12 1 2 3 4 5 6 7 8 9
54
53
52
51
50
48
49
50.2
50.0
49.4
49.5
49.2
50.5
50.1
49.4
49.4
49.7
49.5
49.8
2018年
2019年
【例2-2】已知随机变量 ,其正态分布密度曲线如图所示,若向长方形OABC中随机投掷1点,则该点恰好落在阴影部分的概率为 ( )
A.0.1359
B.0.7282
C.0.8641
D.0.93205
D
附:若随机变量,则
,
.
y
x
2
O
2
B
C
1
A
【例2-3】某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃.下面叙述不正确的是( )
D
A.各月的平均最低气温都在0℃以上
B.七月的平均温差比一月的平均温差大
C.三月和十一月的平均最高气温基本相同
D.平均最高气温高于20℃的月份有5个
一月
二月
三月
四月
五月
六月
七月
八月
九月
十月
十一月
十二月
A
B
20℃
15℃
10℃
5℃
0℃
平均最低气温
平均最高气温
考点3:回归分析
【例3 1】广告投入对商品的销售额有较大影响,某电商对连续5个年度的广告费 x 和销售额 y 进行统计,得到统计数据如下表(单位:万元)
广告费 2 3 4 5 6
销售额 29 41 50 59 71
由上表可得回归方程为 ,据此模型, 预测广告费为10万元时销售额约为( )
A.118.2万元
B.111.2万元
C.108.8万元
D.101.2万元
B
【例3-2】 随着我国中医学的发展,药用昆虫的使用相应愈来愈多.每年春暖以后至寒冬前,是昆虫大量活动与繁殖季节,易于采集各种药用昆虫.已知一只药用昆虫的产卵数y与一定范围内的温度x有关,于是科研人员在3月份的31天中随机挑选了5天进行研究,现收集了该种药用昆虫的5组观测数据如下表:
日期 2日 7日 15日 22日 30日
温度 10 11 13 12 8
产卵数/个 23 25 30 26 16
(1)从这5天中任选2天,记这两天药用昆虫的产卵分别为m,n,求事件“m,n均不小于25”的概率;
日期 2日 7日 15日 22日 30日
温度 10 11 13 12 8
产卵数/个 23 25 30 26 16
(2)科研人员确定的研究方案是:先从这五组数据中任选2组,用剩下的3组数据建立y关于x的线性回归方程,再对被选取的2组数据进行检验.
(ⅰ)若选取的是3月2日与30日的两组数据,请根据3月7日、15日和22日这三天的数据,求出y关于x的线性回归方程;
(ⅱ)若由线性回归方程得到的估计数据与选出的检验数据的误差均不超过2个,则认为得到的线性回归方程是可靠的,试问(ⅰ)中所得的线性回归方程是否可靠?
附:回归直线的斜率和截距的最小二乘估计公式分别为
回归直线过样本点中心 .
2
可以利用回归直线方程预报在x取某个值时y的估计值.
3
1
求回归直线方程的一般步骤:
依据样本数据画出散点图,确定两个变量具有线性相关关系
计算 的值;
计算回归系数;
写出回归直线方程为.
【例4-1】下列四个命题:①在回归模型中,预报变量 y的值不能由解释变量 x唯一确定;②若变量x,y满足关系y=-0.1x+1,且变量y与z正相关,则x与z也正相关;③在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;④以模型 y=cekx 去拟合一组数据时,为了求出回归方程,设z=lny,将其变换后得到线性方程z=0.3x+4,则c=e4,k=0.3.
其中真命题的个数为( )
A.1个 B.2个 C.3个 D.4个
C
【例4-2】已知某种细菌的适宜生长温度为12℃~27℃,为了研究该种细菌的繁殖数量y(单位:个)随温度 (单位:℃)变化的规律,收集数据如下:
温度 /℃ 14 16 18 20 22 24 26
繁殖数量 /个 25 30 38 50 66 120 218
对数据进行初步处理后,得到了一些统计量的值,如表所示:
20 78 4.1 112 3.8 1590 20.5
其中,
(1)请绘出 y 关于x 的散点图,并根据散点图判断 y=bx+a与y=cedx 哪一个更适合作为该种细菌的繁殖数量y 关于温度 x的回归方程类型(给出判断即可,不必说明理由);
14 16 18 20 22 24 26 x/℃
220
200
180
160
140
120
100
80
60
40
20
O
y/个
(2)根据(1)的判断结果及表格数据,建立 y 关于 x 的回归方程(结果精确到0.1);
(3)当温度为27℃时,该种细菌的繁殖数量的预报值为多少?
参考公式:对于一组数据(i=1,2,3,…,n)其回归直线的斜率和截距的最小二乘估计
分别为 ,参考数据: .
考点4:独立性检验
【例5】某社会机构为了调查对手机游戏的兴趣与年龄的关系,通过问卷调查,整理数据得如下2×2列联表:
40岁以下 40岁以上 合计
很有兴趣 30 15 45
无兴趣 20 35 55
合计 50 50 100
(1)根据列联表,能否有99.9%的把握认为对手机游戏的兴趣程度与年龄有关
(2)若已经从40岁以下的被调查者中用分层抽样的方式抽取了5名,现从这5名被调查者中随机选取3名,求这3名被调查 者中恰有1名对手机游戏无兴趣的概率.
参考公式及数据: ,其中n=a+b+c+d.
P(k2≥k0) 0.05 0.010 0.001
k0 3.841 6.635 10.828
独立性检验的关键
根据2×2列联表准确计算K2,若2×2列联表没有列出来,要先列出此表.
01
K2的观测值k越大,对应假设事件H0成立(两类变量相互独立)的概率越小,H0不成立的概率越大.
02
1.用样本估计总体是统计的基本思想.
2.(1)众数、中位数及平均数都是描述一组数据集中趋势的量,平均数是最重要的量,与每个样本数据有关,这是中位数、众数所不具有的性质.
(2)标准差、方差描述了一组数据围绕平均数波动的大小.标准差、方差越大,数据的离散程度就越大.
3.频率分布表和频率分布直方图都可直观描述样本数据的分布规律.
在频率分布直方图中,可分析样本数据的分布情况,大致判断平均数的范围,并利用数据的波动性大小反映方差(标准差)的大小.
4.回归分析是对具有相关关系的两个变量进行统计分析的方法,只有在散点图大致呈线性时,求出的线性回归方程才有实际意义,否则,求出的线性回归方程毫无意义.根据回归方程进行预报,仅是一个预报值,而不是真实发生的值.
再见!
同课章节目录
