2022届高三数学二轮复习数列的综合应用课件(16张ppt)
文档属性
| 名称 | 2022届高三数学二轮复习数列的综合应用课件(16张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-29 12:09:16 | ||
图片预览





文档简介
(共16张PPT)
高三二轮复习
——《数列的综合应用》
大题考法:数列的通项求法、数列求和、等差等比数列综合问题、数列与不等式等,难度中等.
考点1:数列求和问题
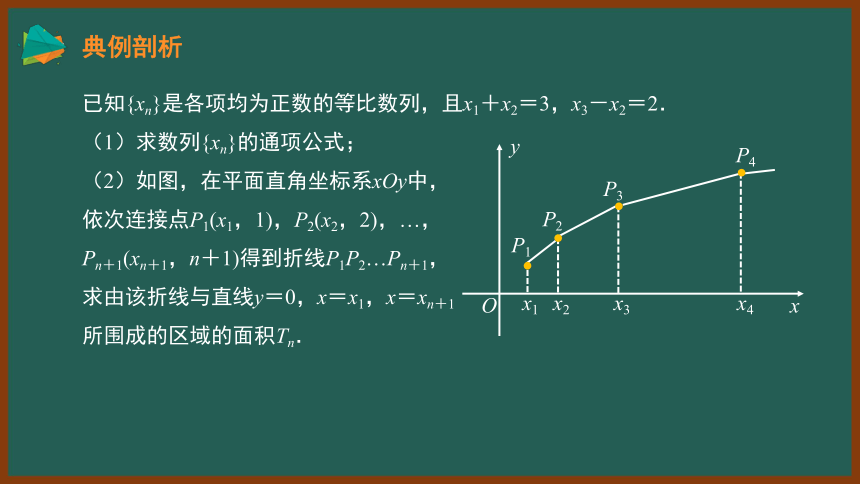
已知{xn}是各项均为正数的等比数列,且x1+x2=3,x3-x2=2.
(1)求数列{xn}的通项公式;
(2)如图,在平面直角坐标系xOy中,
依次连接点P1(x1,1),P2(x2,2),…,
Pn+1(xn+1,n+1)得到折线P1P2…Pn+1,
求由该折线与直线y=0,x=x1,x=xn+1
所围成的区域的面积Tn.
y
O
x
P1
P2
P3
P4
x1
x2
x3
x4
已知{xn}是各项均为正数的等比数列,且x1+x2=3,x3-x2=2.
(1)求数列{xn}的通项公式;
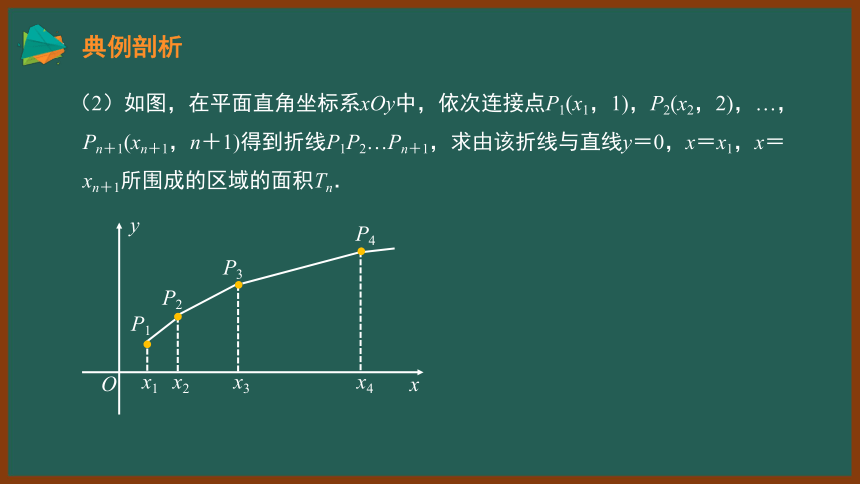
(2)如图,在平面直角坐标系xOy中,依次连接点P1(x1,1),P2(x2,2),…,Pn+1(xn+1,n+1)得到折线P1P2…Pn+1,求由该折线与直线y=0,x=x1,x=xn+1所围成的区域的面积Tn.
y
O
x
P1
P2
P3
P4
x1
x2
x3
x4
数列求和的基本方法
01
公式法
02
分组求和法
03
错位相减法
04
倒序相加法
05
裂项相消法
考点2:数列与不等式综合问题
已知数列{an}满足a1=1,Sn=2an+1,其中Sn为{an}的前n项和(n∈N*).
(1)求S1,S2及数列{Sn}的通项公式;
(2)若数列{bn}满足bn = ,且{bn}的前n项和为Tn,求证:当n≥2时, ≤|Tn|≤ .
已知数列{an}满足a1=1,Sn=2an+1,其中Sn为{an}的前n项和(n∈N*).
(1)求S1,S2及数列{Sn}的通项公式;
(2)若数列{bn}满足bn = ,且{bn}的前n项和为Tn,求证:当n≥2时, ≤|Tn|≤ .
常见的
放缩技巧
1.错位相减法的关注点
适用题型:
等差数列{an}乘以等比数列{bn}对应项得到的数列{an·bn}求和.
01
步骤:
求和时先乘以数列{bn}的公比.
把两个和的形式错位相减.
整理结果形式.
02
2.裂项求和的常见技巧
如果是证明不等式,常转化为数列和的最值问题,同时要注意比较法、放缩法、基本不等式的应用;
如果是解不等式,注意因式分解的应用.
3.数列与不等式综合问题
再见!
高三二轮复习
——《数列的综合应用》
大题考法:数列的通项求法、数列求和、等差等比数列综合问题、数列与不等式等,难度中等.
考点1:数列求和问题
已知{xn}是各项均为正数的等比数列,且x1+x2=3,x3-x2=2.
(1)求数列{xn}的通项公式;
(2)如图,在平面直角坐标系xOy中,
依次连接点P1(x1,1),P2(x2,2),…,
Pn+1(xn+1,n+1)得到折线P1P2…Pn+1,
求由该折线与直线y=0,x=x1,x=xn+1
所围成的区域的面积Tn.
y
O
x
P1
P2
P3
P4
x1
x2
x3
x4
已知{xn}是各项均为正数的等比数列,且x1+x2=3,x3-x2=2.
(1)求数列{xn}的通项公式;
(2)如图,在平面直角坐标系xOy中,依次连接点P1(x1,1),P2(x2,2),…,Pn+1(xn+1,n+1)得到折线P1P2…Pn+1,求由该折线与直线y=0,x=x1,x=xn+1所围成的区域的面积Tn.
y
O
x
P1
P2
P3
P4
x1
x2
x3
x4
数列求和的基本方法
01
公式法
02
分组求和法
03
错位相减法
04
倒序相加法
05
裂项相消法
考点2:数列与不等式综合问题
已知数列{an}满足a1=1,Sn=2an+1,其中Sn为{an}的前n项和(n∈N*).
(1)求S1,S2及数列{Sn}的通项公式;
(2)若数列{bn}满足bn = ,且{bn}的前n项和为Tn,求证:当n≥2时, ≤|Tn|≤ .
已知数列{an}满足a1=1,Sn=2an+1,其中Sn为{an}的前n项和(n∈N*).
(1)求S1,S2及数列{Sn}的通项公式;
(2)若数列{bn}满足bn = ,且{bn}的前n项和为Tn,求证:当n≥2时, ≤|Tn|≤ .
常见的
放缩技巧
1.错位相减法的关注点
适用题型:
等差数列{an}乘以等比数列{bn}对应项得到的数列{an·bn}求和.
01
步骤:
求和时先乘以数列{bn}的公比.
把两个和的形式错位相减.
整理结果形式.
02
2.裂项求和的常见技巧
如果是证明不等式,常转化为数列和的最值问题,同时要注意比较法、放缩法、基本不等式的应用;
如果是解不等式,注意因式分解的应用.
3.数列与不等式综合问题
再见!
同课章节目录
