2022届高三数学二轮复习三角恒等变换与解三角形课件(18张ppt)
文档属性
| 名称 | 2022届高三数学二轮复习三角恒等变换与解三角形课件(18张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-29 12:07:27 | ||
图片预览



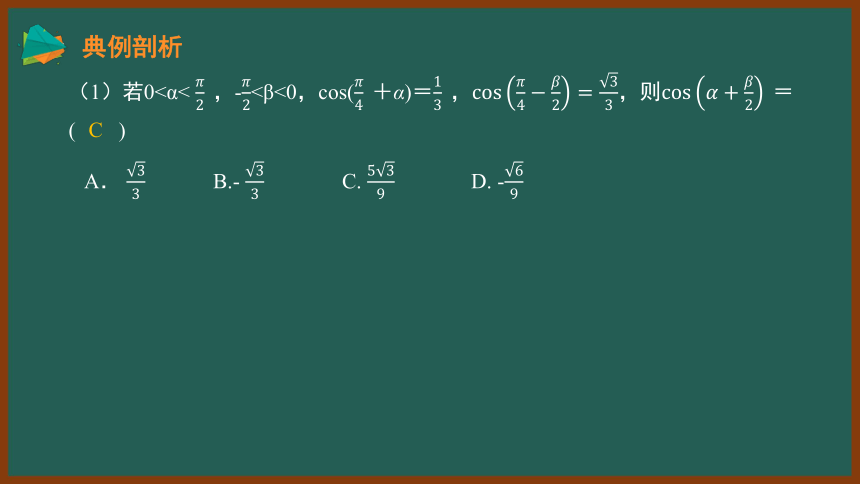



文档简介
(共18张PPT)
高三二轮复习
——《三角恒等变换与解三角形》
2.大题考法:三角函数的化简与求值、图象与性质、解三角形(面积问题、周长问题、最值问题),难度中等.
1.小题考法:三角函数的化简与求值、判定三角形形状、解三角形,难度中等.
考点1:三角恒等变换与求值
(1)若0<α< ,-<β<0,cos(+α)=,,则= ( )
A. B.- C. D. -
C
(2)如图,圆O与x轴的正半轴的交点为A,点C,B在圆O上,且点C位于第一象限,点B的坐标为,∠AOC=α.若|BC|=1,则的值为________.
O
x
y
A
B
C
α
考点2:正、余弦定理
(1)△ABC的内角A,B,C的对边分别为a,b,c.已知sin B+sin A(sin C-cos C)=0,a=2,c=,则C= ( )
A. B. C. D.
B
(2)在△ABC中,内角A,B,C所对的边分别为a,b,c,若a2=b2+c2-bc,且sin B=cos C,则下列结论中正确的是 ( )
A. B.c=2a
D
C. D. △ABC是等边三角形
(3)在△ABC中,B=30°,AC=,D是AB边上的一点,CD=2,若∠ACD为锐角,△ACD的面积为4,则BC=________.
4
A
C
B
30°
D
解三角形问题的求解策略
已知条件 解题思路
两角A,B与一边a
两边b,c及其夹角A a2=b2+c2 2bccos A
三边a,b,c 由余弦定理可求出角A,B,C
两边a,b及其中一边的对角A
考点3:正、余弦定理的实际应用
某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:在C处(点C在水平地面下方,O为CH与水平地面ABO的交点)进行该仪器的垂直弹射,水平地面上两个观察点A,B两地相距100米,∠BAC=60°,其中A到C的距离比B到C的距离远40米.A地测得该仪器在C处的俯角为∠OAC=15°,A地测得最高点H的仰角为∠HAO=30°,则该仪器的垂直弹射高度CH为 ( )
B
A. 米 B . 140 米C .210 米 D . 米
B
H
A
C
O
解三角形实际问题的常见类型及解题思路
实际问题经抽象概括后,已知量与未知量全部集中在一个三角形中,可用正弦定理或余弦定理求解.
实际问题经抽象概括后,已知量与未知量涉及两个或两个以上的三角形,这时需作出这些三角形,先解已知条件的三角形,然后逐步求解其他三角形,有时需设出未知量,从几个三角形中列出方程(组),解方程(组)得出所要求的解.
考点4:解三角形与三角函数交汇
已知函数f(x)= sin xcos x-2cos2x-1,x∈R.
(1)求函数f(x)的最小正周期和最小值;
(2)在△ABC中,A,B,C的对边分别为a,b,c,已知c=,f(C)=0,sin B=2sin A,求a,b的值.
已知函数f(x)= sin xcos x-2cos2x-1,x∈R.
(1)求函数f(x)的最小正周期和最小值;
(2)在△ABC中,A,B,C的对边分别为a,b,c,已知c=,f(C)=0,sin B=2sin A,求a,b的值.
再见!
高三二轮复习
——《三角恒等变换与解三角形》
2.大题考法:三角函数的化简与求值、图象与性质、解三角形(面积问题、周长问题、最值问题),难度中等.
1.小题考法:三角函数的化简与求值、判定三角形形状、解三角形,难度中等.
考点1:三角恒等变换与求值
(1)若0<α< ,-<β<0,cos(+α)=,,则= ( )
A. B.- C. D. -
C
(2)如图,圆O与x轴的正半轴的交点为A,点C,B在圆O上,且点C位于第一象限,点B的坐标为,∠AOC=α.若|BC|=1,则的值为________.
O
x
y
A
B
C
α
考点2:正、余弦定理
(1)△ABC的内角A,B,C的对边分别为a,b,c.已知sin B+sin A(sin C-cos C)=0,a=2,c=,则C= ( )
A. B. C. D.
B
(2)在△ABC中,内角A,B,C所对的边分别为a,b,c,若a2=b2+c2-bc,且sin B=cos C,则下列结论中正确的是 ( )
A. B.c=2a
D
C. D. △ABC是等边三角形
(3)在△ABC中,B=30°,AC=,D是AB边上的一点,CD=2,若∠ACD为锐角,△ACD的面积为4,则BC=________.
4
A
C
B
30°
D
解三角形问题的求解策略
已知条件 解题思路
两角A,B与一边a
两边b,c及其夹角A a2=b2+c2 2bccos A
三边a,b,c 由余弦定理可求出角A,B,C
两边a,b及其中一边的对角A
考点3:正、余弦定理的实际应用
某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:在C处(点C在水平地面下方,O为CH与水平地面ABO的交点)进行该仪器的垂直弹射,水平地面上两个观察点A,B两地相距100米,∠BAC=60°,其中A到C的距离比B到C的距离远40米.A地测得该仪器在C处的俯角为∠OAC=15°,A地测得最高点H的仰角为∠HAO=30°,则该仪器的垂直弹射高度CH为 ( )
B
A. 米 B . 140 米C .210 米 D . 米
B
H
A
C
O
解三角形实际问题的常见类型及解题思路
实际问题经抽象概括后,已知量与未知量全部集中在一个三角形中,可用正弦定理或余弦定理求解.
实际问题经抽象概括后,已知量与未知量涉及两个或两个以上的三角形,这时需作出这些三角形,先解已知条件的三角形,然后逐步求解其他三角形,有时需设出未知量,从几个三角形中列出方程(组),解方程(组)得出所要求的解.
考点4:解三角形与三角函数交汇
已知函数f(x)= sin xcos x-2cos2x-1,x∈R.
(1)求函数f(x)的最小正周期和最小值;
(2)在△ABC中,A,B,C的对边分别为a,b,c,已知c=,f(C)=0,sin B=2sin A,求a,b的值.
已知函数f(x)= sin xcos x-2cos2x-1,x∈R.
(1)求函数f(x)的最小正周期和最小值;
(2)在△ABC中,A,B,C的对边分别为a,b,c,已知c=,f(C)=0,sin B=2sin A,求a,b的值.
再见!
同课章节目录
