2022届高三数学二轮复习平面向量课件(16张ppt)
文档属性
| 名称 | 2022届高三数学二轮复习平面向量课件(16张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-29 12:09:41 | ||
图片预览






文档简介
(共16张PPT)
高三二轮复习
——《平面向量》
2.大题考法:向量作为工具常与三角函数、解三角形、不等式、解析几何等结合,以解答题形式出现.
1.小题考法:考查向量的线性运算、数量积运算,多以熟知的平面图形为背景进行命题,难度中低档;
考点1:平面向量的线性运算
(1)如图,正方形ABCD中,M,N分别是BC,CD的中点,若,则λ+μ= ( )
A.2 B. C. D.
D
N
D
C
A
B
M
x
y
(1)如图,正方形ABCD中,M,N分别是BC,CD的中点,若,则λ+μ= ( )
A.2 B. C. D.
D
N
D
C
A
B
M
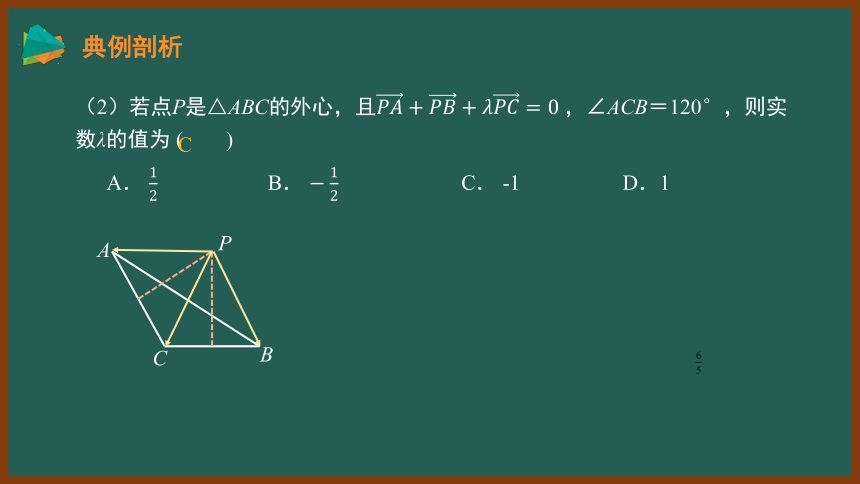
(2)若点P是△ABC的外心,且,∠ACB=120°,则实数λ的值为 ( )
A. B. C. -1 D.1
C
A
C
B
P
平面向量线性技巧
对于平面向量的线性运算问题,要尽可能转化到三角形或平行四边形中,灵活运用三角形法则、平行四边形法则,紧密结合图形的几何性质进行运算.
在证明两向量平行时,若已知两向量的坐标形式,常利用坐标运算来判断;若两向量不是以坐标形式呈现的,常利用共线向量定理来判断.
考点2:平面向量数量积
(1)如图,在△ABC中,AD⊥AB, , |,则的值为( )
D
A. B. C. D.
A
B
C
D
(2)平面向量,满足||=4,||=2, +在上的投影为5,则| -2|的模为( )
B
A. 2 B.4 C. 8 D.16
(3)已知正方形ABCD的边长为1,点E是AB边上的动点,则· 的值为________; · 的最大值为________.
D
C
A
B
E
x
y
1
1
(3)已知正方形ABCD的边长为1,点E是AB边上的动点,则· 的值为________; · 的最大值为________.
D
C
A
B
E
1
1
利用不等式求最值的解题技巧
在求解与向量的模有关的问题时,往往会涉及“平方”技巧,注意对结论(± )2=| |2+| |2±2 · ,(+ + )2=| |2+| |2+| |2+2(· + · + · )的灵活运用.另外,向量作为工具性的知识,具备代数和几何两种特征,求解此类问题时可以使用数形结合的思想,从而加快解题速度.
1.平面向量的数量积的运算有两种形式:
(1)依据模和夹角计算,要注意确定这两个向量的夹角,如夹角不易求或者不可求,可通过选择易求夹角和模的基底进行转化;
(2)利用坐标来计算,向量的平行和垂直都可以转化为坐标满足的等式,从而应用方程思想解决问题,化形为数,使向量问题数量化.
2.根据平行四边形法则,对于非零向量a,b,当|a+b|=|a-b|时,平行四边形的两条对角线长度相等,此时平行四边形是矩形,条件|a+b|=|a-b|等价于向量a,b互相垂直.
3.两个向量夹角的范围是[0,π],在使用平面向量解决问题时要特别注意两个向量夹角可能是0或π的情况,如已知两个向量的夹角为钝角时,不单纯就是其数量积小于零,还要求不能反向共线.
再见!
高三二轮复习
——《平面向量》
2.大题考法:向量作为工具常与三角函数、解三角形、不等式、解析几何等结合,以解答题形式出现.
1.小题考法:考查向量的线性运算、数量积运算,多以熟知的平面图形为背景进行命题,难度中低档;
考点1:平面向量的线性运算
(1)如图,正方形ABCD中,M,N分别是BC,CD的中点,若,则λ+μ= ( )
A.2 B. C. D.
D
N
D
C
A
B
M
x
y
(1)如图,正方形ABCD中,M,N分别是BC,CD的中点,若,则λ+μ= ( )
A.2 B. C. D.
D
N
D
C
A
B
M
(2)若点P是△ABC的外心,且,∠ACB=120°,则实数λ的值为 ( )
A. B. C. -1 D.1
C
A
C
B
P
平面向量线性技巧
对于平面向量的线性运算问题,要尽可能转化到三角形或平行四边形中,灵活运用三角形法则、平行四边形法则,紧密结合图形的几何性质进行运算.
在证明两向量平行时,若已知两向量的坐标形式,常利用坐标运算来判断;若两向量不是以坐标形式呈现的,常利用共线向量定理来判断.
考点2:平面向量数量积
(1)如图,在△ABC中,AD⊥AB, , |,则的值为( )
D
A. B. C. D.
A
B
C
D
(2)平面向量,满足||=4,||=2, +在上的投影为5,则| -2|的模为( )
B
A. 2 B.4 C. 8 D.16
(3)已知正方形ABCD的边长为1,点E是AB边上的动点,则· 的值为________; · 的最大值为________.
D
C
A
B
E
x
y
1
1
(3)已知正方形ABCD的边长为1,点E是AB边上的动点,则· 的值为________; · 的最大值为________.
D
C
A
B
E
1
1
利用不等式求最值的解题技巧
在求解与向量的模有关的问题时,往往会涉及“平方”技巧,注意对结论(± )2=| |2+| |2±2 · ,(+ + )2=| |2+| |2+| |2+2(· + · + · )的灵活运用.另外,向量作为工具性的知识,具备代数和几何两种特征,求解此类问题时可以使用数形结合的思想,从而加快解题速度.
1.平面向量的数量积的运算有两种形式:
(1)依据模和夹角计算,要注意确定这两个向量的夹角,如夹角不易求或者不可求,可通过选择易求夹角和模的基底进行转化;
(2)利用坐标来计算,向量的平行和垂直都可以转化为坐标满足的等式,从而应用方程思想解决问题,化形为数,使向量问题数量化.
2.根据平行四边形法则,对于非零向量a,b,当|a+b|=|a-b|时,平行四边形的两条对角线长度相等,此时平行四边形是矩形,条件|a+b|=|a-b|等价于向量a,b互相垂直.
3.两个向量夹角的范围是[0,π],在使用平面向量解决问题时要特别注意两个向量夹角可能是0或π的情况,如已知两个向量的夹角为钝角时,不单纯就是其数量积小于零,还要求不能反向共线.
再见!
同课章节目录
