2022届高三数学二轮复习立体几何中的向量方法课件(18张ppt)
文档属性
| 名称 | 2022届高三数学二轮复习立体几何中的向量方法课件(18张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-29 12:10:27 | ||
图片预览




文档简介
(共18张PPT)
高三二轮复习
《立体几何中的向量方法》
大题
考法
考查平行、垂直关系的证明
空间角的计算
几何体体积的计算
1
2
3
考点1:利用空间向量证明平行、垂直关系
P
A
B
C
D
E
x
y
z
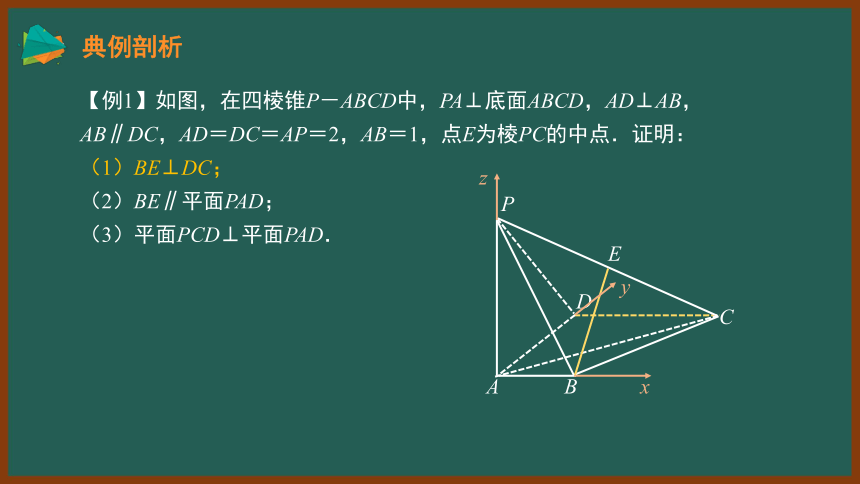
【例1】如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.证明:
(1)BE⊥DC;
(2)BE∥平面PAD;
(3)平面PCD⊥平面PAD.
P
A
B
C
D
E
x
y
z
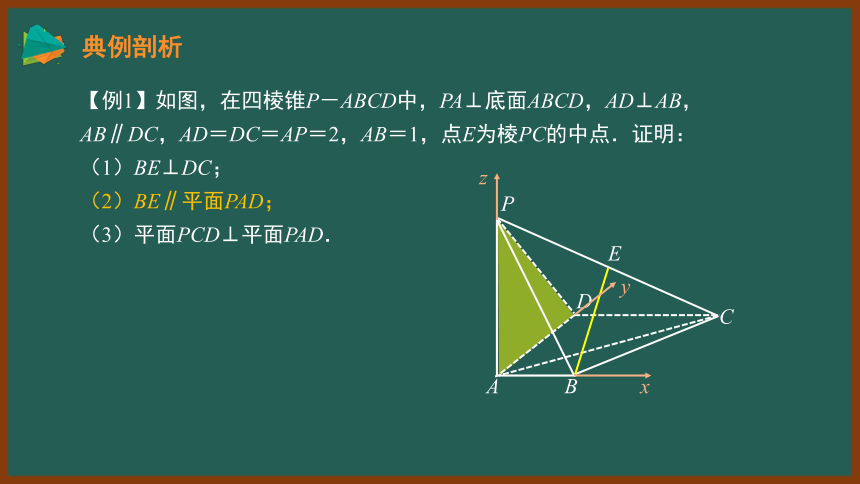
【例1】如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.证明:
(1)BE⊥DC;
(2)BE∥平面PAD;
(3)平面PCD⊥平面PAD.
P
A
B
C
D
x
y
z
【例1】如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.证明:
(1)BE⊥DC;
(2)BE∥平面PAD;
(3)平面PCD⊥平面PAD.
考点2:利用空间向量计算空间角
【例2】如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(1)证明:MN∥平面PAB;
(2)求直线AN与平面PMN所成角的正弦值.
A
B
P
D
C
M
N
T
【例2】如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(1)证明:MN∥平面PAB;
(2)求直线AN与平面PMN所成角的正弦值.
A
B
P
D
C
M
N
E
x
y
z
【例3】如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= AD,∠BAD=∠ABC=90°,E是PD的中点.
(1)证明:直线CE∥平面PAB;
(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D
的余弦值.
P
E
D
C
B
A
F
【例3】如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= AD,∠BAD=∠ABC=90°,E是PD的中点.
(1)证明:直线CE∥平面PAB;
(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D
的余弦值.
P
M
D
C
B
A
x
y
z
考点3:利用空间向量求解探索性问题
【例4】如图,C是以AB为直径的圆O上异于A,B的点,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E,F分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.
(1)证明:直线l⊥平面PAC;
(2)直线l上是否存在点Q,使直线PQ分别与
平面AEF、直线EF所成的角互余?若存在,求
出AQ的长;若不存在,请说明理由.
P
E
F
A
B
C
【例4】如图,C是以AB为直径的圆O上异于A,B的点,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E,F分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.
(1)证明:直线l⊥平面PAC;
(2)直线l上是否存在点Q,使直线PQ分别与
平面AEF、直线EF所成的角互余?若存在,求
出AQ的长;若不存在,请说明理由.
P
E
F
A
B
C
x
y
z
异面直线所成角的求法
异面直线 l1与l2 所成角θ 向量 与 所成角φ 图形
范围
求法
l1
l2
直线与平面所成角的求法
直线 l 与平面 α所成角θ 向量 与 所成角φ 图形
范围
求法
l
α
θ
φ
l
α
θ
φ
二面角的平面角的求法
二面角 α–l–β的平面角θ 法向量 与 所成角φ 图形
范围
求法
cos θ=cos φ或cos θ=-cos φ
α
β
l
θ
α
β
l
θ
再见!
高三二轮复习
《立体几何中的向量方法》
大题
考法
考查平行、垂直关系的证明
空间角的计算
几何体体积的计算
1
2
3
考点1:利用空间向量证明平行、垂直关系
P
A
B
C
D
E
x
y
z
【例1】如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.证明:
(1)BE⊥DC;
(2)BE∥平面PAD;
(3)平面PCD⊥平面PAD.
P
A
B
C
D
E
x
y
z
【例1】如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.证明:
(1)BE⊥DC;
(2)BE∥平面PAD;
(3)平面PCD⊥平面PAD.
P
A
B
C
D
x
y
z
【例1】如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.证明:
(1)BE⊥DC;
(2)BE∥平面PAD;
(3)平面PCD⊥平面PAD.
考点2:利用空间向量计算空间角
【例2】如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(1)证明:MN∥平面PAB;
(2)求直线AN与平面PMN所成角的正弦值.
A
B
P
D
C
M
N
T
【例2】如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(1)证明:MN∥平面PAB;
(2)求直线AN与平面PMN所成角的正弦值.
A
B
P
D
C
M
N
E
x
y
z
【例3】如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= AD,∠BAD=∠ABC=90°,E是PD的中点.
(1)证明:直线CE∥平面PAB;
(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D
的余弦值.
P
E
D
C
B
A
F
【例3】如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= AD,∠BAD=∠ABC=90°,E是PD的中点.
(1)证明:直线CE∥平面PAB;
(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D
的余弦值.
P
M
D
C
B
A
x
y
z
考点3:利用空间向量求解探索性问题
【例4】如图,C是以AB为直径的圆O上异于A,B的点,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E,F分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.
(1)证明:直线l⊥平面PAC;
(2)直线l上是否存在点Q,使直线PQ分别与
平面AEF、直线EF所成的角互余?若存在,求
出AQ的长;若不存在,请说明理由.
P
E
F
A
B
C
【例4】如图,C是以AB为直径的圆O上异于A,B的点,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E,F分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.
(1)证明:直线l⊥平面PAC;
(2)直线l上是否存在点Q,使直线PQ分别与
平面AEF、直线EF所成的角互余?若存在,求
出AQ的长;若不存在,请说明理由.
P
E
F
A
B
C
x
y
z
异面直线所成角的求法
异面直线 l1与l2 所成角θ 向量 与 所成角φ 图形
范围
求法
l1
l2
直线与平面所成角的求法
直线 l 与平面 α所成角θ 向量 与 所成角φ 图形
范围
求法
l
α
θ
φ
l
α
θ
φ
二面角的平面角的求法
二面角 α–l–β的平面角θ 法向量 与 所成角φ 图形
范围
求法
cos θ=cos φ或cos θ=-cos φ
α
β
l
θ
α
β
l
θ
再见!
同课章节目录
