2022届高三数学二轮复习等差等比数列的基本问题课件(21张ppt)
文档属性
| 名称 | 2022届高三数学二轮复习等差等比数列的基本问题课件(21张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-29 12:16:51 | ||
图片预览



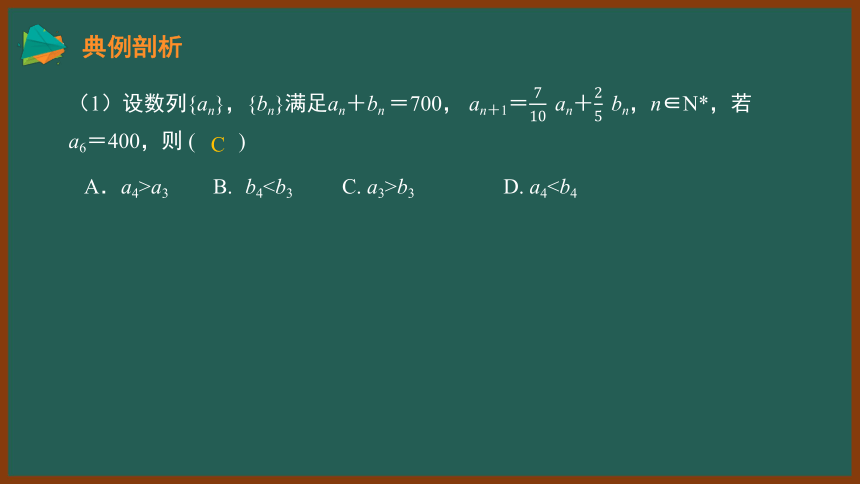





文档简介
(共21张PPT)
高三二轮复习
——《等差数列、等比数列
的基本问题》
2.大题考法:数列的通项也是高考热点,常在解答题中的第(1)问出现,难度中档以下.
1.小题考法:等差、等比数列基本运算和性质,难度中等偏下.
考点1:数列的递推公式
(1)设数列{an},{bn}满足an+bn =700, an+1=an+bn,n∈N*,若a6=400,则 ( )
A.a4>a3 B. b4b3 D. a4C
(2)设数列{an}的前n项和为Sn,若a1=1,an+1=Sn(n∈N*),则通项公式an=____________.
(3)设数列{an}的前n项和为Sn,且a1=1, 对一切n∈N*都成立,则a2=________, =________.
2
2
由递推关系式求通项公式的常用方法
已知a1且an-an-1=f(n),可用“累加法”求an .
已知a1且= f(n) ,可用“累乘法”求an .
Sn与an关系问题的求解思路
利用an =Sn-Sn-1(n≥2)转化为只含Sn ,Sn-1的关系式,再求解.
利用Sn -Sn-1 =an(n≥2)转化为只含an , an-1的关系式,再求解.
考点2:等差等比数列
的基本量计算
(1)已知等差数列{an}满足an + an+1=2n-3,n∈N*,则a1+a2+a6+a7=________,数列{an}的前n项和Sn=________.
8
(2)设等比数列{an}满足a1+a3=10,a2+a4=5,则a1a2…an的最大值为________.
64
等差(比)数列基本运算的
解题途径
设基本量a1和公差d(公比q).
列、解方程组:把条件转化为关于a1和d(q)的方程(组),然后求解,注意整体计算,以减少运算量.
考点3:等差(比)数列的性质
(1)已知等差数列{an},Sn表示前n项的和,a5+a11>0,a6+a9<0,则满足Sn <0的正整数n的最大值是 ( )
A.12 B. 13 C. 14 D. 15
C
(2)已知数列{an}的前n项和为Sn,且满足Sn=2an -2,若数列{bn}满足bn =10-,则使数列{bn}的前n项和取最大值时的n的值为________.
9或10
等差(比)性质应用注意事项
利用等差(比)性质求解的关键是抓住项与项之间的关系及项的序号之间的关系,从这些特点入手选择恰当的性质进行求解.
活用函数性质:数列是一种特殊的函数,具有函数的一些性质,如单调性、周期性等,可利用函数的性质解题.
考点4:等差数列与等比数列
的综合问题
(1)等差数列{an}的前n项和为Sn ,已知S10=0,S15=25,则nSn 的最小值为( )
A.-47 B. -48 C. -49 D. -50
C
(2)已知a1,a2,a3,a4成等比数列,且a1+a2+a3+a4=ln(a1+a2+a3),若a1>1,则( )
A. a1a3,a2C. a1a4 D. a1>a3,a2>a4
B
等差(比)数列综合问题求解策略
对于等差数列与等比数列交汇的问题,要从两个数列的特征入手,理清它们的关系,常用“基本量法”求解,但有时灵活地运用等差中项、等比中项等性质,可使运算简便.
数列的通项或前n项和可以看作关于n的函数,然后利用函数的性质求解数列的有关最值问题.
等差、等比数列与不等式交汇的问题常构造函数,根据函数的性质解不等式.
再见!
高三二轮复习
——《等差数列、等比数列
的基本问题》
2.大题考法:数列的通项也是高考热点,常在解答题中的第(1)问出现,难度中档以下.
1.小题考法:等差、等比数列基本运算和性质,难度中等偏下.
考点1:数列的递推公式
(1)设数列{an},{bn}满足an+bn =700, an+1=an+bn,n∈N*,若a6=400,则 ( )
A.a4>a3 B. b4
(2)设数列{an}的前n项和为Sn,若a1=1,an+1=Sn(n∈N*),则通项公式an=____________.
(3)设数列{an}的前n项和为Sn,且a1=1, 对一切n∈N*都成立,则a2=________, =________.
2
2
由递推关系式求通项公式的常用方法
已知a1且an-an-1=f(n),可用“累加法”求an .
已知a1且= f(n) ,可用“累乘法”求an .
Sn与an关系问题的求解思路
利用an =Sn-Sn-1(n≥2)转化为只含Sn ,Sn-1的关系式,再求解.
利用Sn -Sn-1 =an(n≥2)转化为只含an , an-1的关系式,再求解.
考点2:等差等比数列
的基本量计算
(1)已知等差数列{an}满足an + an+1=2n-3,n∈N*,则a1+a2+a6+a7=________,数列{an}的前n项和Sn=________.
8
(2)设等比数列{an}满足a1+a3=10,a2+a4=5,则a1a2…an的最大值为________.
64
等差(比)数列基本运算的
解题途径
设基本量a1和公差d(公比q).
列、解方程组:把条件转化为关于a1和d(q)的方程(组),然后求解,注意整体计算,以减少运算量.
考点3:等差(比)数列的性质
(1)已知等差数列{an},Sn表示前n项的和,a5+a11>0,a6+a9<0,则满足Sn <0的正整数n的最大值是 ( )
A.12 B. 13 C. 14 D. 15
C
(2)已知数列{an}的前n项和为Sn,且满足Sn=2an -2,若数列{bn}满足bn =10-,则使数列{bn}的前n项和取最大值时的n的值为________.
9或10
等差(比)性质应用注意事项
利用等差(比)性质求解的关键是抓住项与项之间的关系及项的序号之间的关系,从这些特点入手选择恰当的性质进行求解.
活用函数性质:数列是一种特殊的函数,具有函数的一些性质,如单调性、周期性等,可利用函数的性质解题.
考点4:等差数列与等比数列
的综合问题
(1)等差数列{an}的前n项和为Sn ,已知S10=0,S15=25,则nSn 的最小值为( )
A.-47 B. -48 C. -49 D. -50
C
(2)已知a1,a2,a3,a4成等比数列,且a1+a2+a3+a4=ln(a1+a2+a3),若a1>1,则( )
A. a1
B
等差(比)数列综合问题求解策略
对于等差数列与等比数列交汇的问题,要从两个数列的特征入手,理清它们的关系,常用“基本量法”求解,但有时灵活地运用等差中项、等比中项等性质,可使运算简便.
数列的通项或前n项和可以看作关于n的函数,然后利用函数的性质求解数列的有关最值问题.
等差、等比数列与不等式交汇的问题常构造函数,根据函数的性质解不等式.
再见!
同课章节目录
