福建省三明一中2012-2013学年高一上学期期中考试数学试题
文档属性
| 名称 | 福建省三明一中2012-2013学年高一上学期期中考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 287.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-22 14:35:38 | ||
图片预览



文档简介
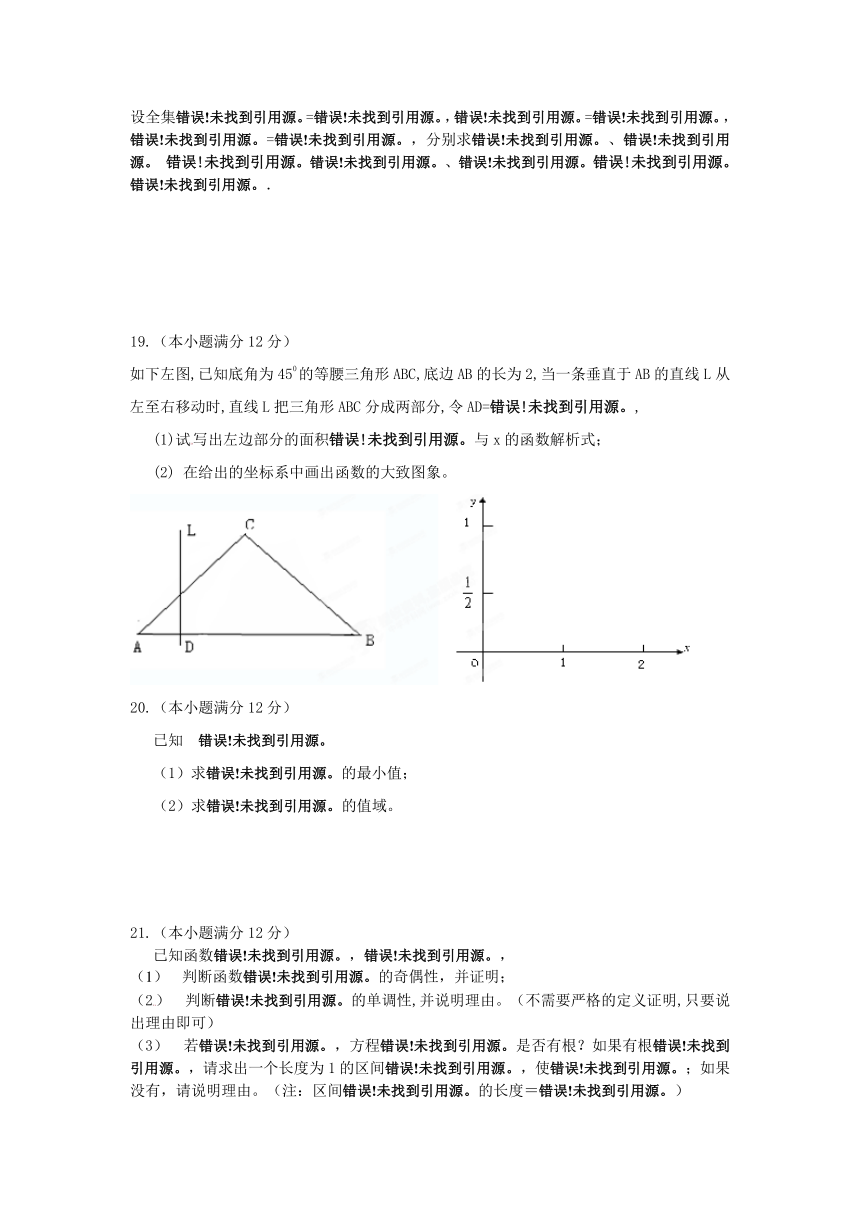
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,在答题卷相应题目的答题区域内作答.
1. 函数,则
A.1 B.2 C.3 D.4
2.下列角为第二象限角的是
A. B. C. D.
3. 如图所示,不可能表示函数的是4. 若幂函数的图象过点,则为
A. B. C.1 D.2
5. 下列四个函数,不在区间[1,2]上单调递减的是
A. B. C. D.
6. 函数在下列哪个区间内有零点
A. B. C. D.
7.如右图,函数的图象是曲线OAB,其中点O、A、B的
坐标分别是(0,0),(1,2),(3,1),则的值是
A.1 B.2 C.3 D.无法判断
8. 函数是定义在R上的偶函数,当时,,那么当时,的解析式是
A. B. C. D.
9.一批设备价值a万元,由于使用磨损,每年比上一年价值降低b% ,n年以后这批设备的价值为
A. B. C. D.
10.为第四象限角,,则=
A. B. C. D.
11.函数的单调递增区间是
A. B. C. D.
12. 若为奇函数,在上单调递增,且,则的解集为
A. B.
C. D.
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分.在答题卷相应题目的答题区域内作答
13.= ** .
14.= **
15. 将、、按从小到大排列为 ** .
16. 用符号“”表示不超过x的最大整数,如,设集合,则 ** .
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.在答题卷相应题目的答题区域内作答
17.(本小题满分12分)
(1) 已知角的终边上有一点,求的值;
(2) 已知的值。
18.(本小题满分12分)
设全集=,=, =,分别求、 、.
19.(本小题满分12分)
如下左图,已知底角为450的等腰三角形ABC,底边AB的长为2,当一条垂直于AB的直线L从左至右移动时,直线L把三角形ABC分成两部分,令AD=,
(1)试写出左边部分的面积与x的函数解析式;
(2) 在给出的坐标系中画出函数的大致图象。
20.(本小题满分12分)
已知
(1)求的最小值;
(2)求的值域。
21.(本小题满分12分)
已知函数,,
判断函数的奇偶性,并证明;
(2) 判断的单调性,并说明理由。(不需要严格的定义证明,只要说出理由即可)
(3) 若,方程是否有根?如果有根,请求出一个长度为1的区间,使;如果没有,请说明理由。(注:区间的长度=)
22.(本小题满分14分)
设为奇函数,为常数.
(1)求的值;
(2)求的值;
(3)若对于区间[3,4]上的每一个的值,不等式>恒成立,求实数的取值范围.
三明一中2012-13上学期学段考
高一数学答案
一、选择题
BBDC DABB CBAD
二、填空题
13、; 14、2; 15、; 16、
三、解答题
17、(1)已知角的终边上有一点,求的值
(2)已知的值。
(2)∵
∴ ,解得………………………………12分
18、设全集=,=, =,分别求、 、.
解∵ ==…………………………………2分
又 == …………………………………4分
== …………………………………6分
∴ = , …………………………………8分
= , …………………………………10分
= …………………………………12分
19、如下左图,已知底角为450的等腰三角形ABC,底边AB的长为2,当一条垂直于AB的直线L从左至右移动时,直线L把三角形ABC分成两部分,令AD=,
(1) 试写出左边部分的面积与x的函数解析式;
(2) 在给出的坐标系中画出函数的大致图象。
∴ ………………………………………7分
…………………………………12分
20、已知 ,
(1)求的最小值; (2)求的值域
(2) ∵ =(
………………………………………………8分
设则
则……………………………………………10分
所以可知当时,即时,
当 ,即或4时,
∴ 的值域为……………………………12分
21、已知函数,,
判断函数的奇偶性,并证明;
(2) 判断的单调性,并说明理由。(不需要严格的定义证明,只要说出理由即可)
(3) 若,方程是否有根?如果有根,请求出一个长度为1的区间,使;如果没有,请说明理由。(注:区间的长度=)
所以可知为奇函数……………………………………………4分
(2) ∵=
① 当时,单调递增,单调递减,
所以单调递增…………………………………………………6分
②当时,单调递减,单调递增,
所以单调递减。
综上可知时,单调递增;,单调递减。
………………………………………………8分
(3)当,,又
设…………………………………9分
∵ ………………………………………………10分
∴ ,故存在零点
即方程有根……………………………………………12分
22、设为奇函数,为常数.
(1)求的值;
(2)求的值
(2)若对于区间[3,4]上的每一个的值,不等式>恒成立,求实数的取值范围.
故,解得 ………………………4分
显然不成立,舍去。所以 ………………………………………5分
(2)由(1)知
∴=……6分
=………………………9分
(3)依题意 对于区间[3,4]上的每一个的值,不等式>恒成立
则 当恒成立…………………10分
又 …………………11分
∵在[3,4]上单调递增,单调递减
所以在[3,4]上单调递增 …………………………………………12分
∴ 只需即可
又 所以 ……………………………………………14分
53
同课章节目录
