椭圆中有关定值问题课件-2022届高三数学二轮专题(共20张PPT)
文档属性
| 名称 | 椭圆中有关定值问题课件-2022届高三数学二轮专题(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-03 22:27:14 | ||
图片预览







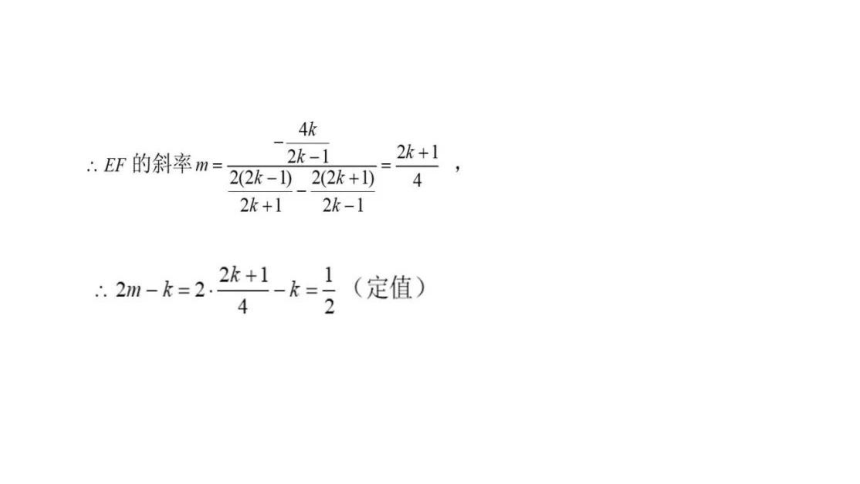
文档简介
(共20张PPT)
椭圆中有关定值问题
单击输入您的封面副标题
二、经典例题
方法二 引入斜率参数法
变式拓展
方法一 引入点参数
方法二 引入斜率参数法
练习:
方法总结
背景介绍
解析几何″因其运算繁难,“要想高考好、解几很重要”,自然成为我们备
战高考的重点,而椭圆中的定值问题又是解析几何命题的热点,2012年江
苏卷,2018年全国卷都作为难题出现。“动中求定”,因其“动”,这类问题
中的变量较多变量间的关系式也复杂,对我们分析能力、运算能力都有比
较高的要求。但是,如果我们透视定值问题的本质,解决的通法是“引参制
动〃,即引入适切的变量,把要求的量用它表示出来,再探索其“定〃的特质
例1.如图,在平面直角坐标系xOy中,椭圆
1,若点A,B分别是椭圆的
左、右顶点,直线1经过点B且垂直于x轴,点P是椭圆上异于A,B的任意一点,
直线AP交1于点M,若直线OM的斜率为k1,直线BP的斜率为k2,求证:kk2
为定值
方法一引入点参数
详解:设P(x,y)(y1≠0),M(2y3),则k=2,k2=-当
x
AP,M三点共线,所以y
4
y1
X,-+
所以起2=-J0y14y
2(x-2)2(x2-4)
因为点P(x,y1)在椭圆上,所以4y2=3(4-x
故kk2
4
为定值
(x2-4)2
详解:由题意知直线AP的斜率存在且不为零,设直线AP:y=k(x+2)
M
y=k(x+2)
由
,消去y得(3+4k2)x2+16k2x+16k2-12
又x4=-2,所以x
6-8k212k
3+4k
3+4k2°3+4k2
在直线中令x=2得yx=4k,∴M(2,4k)
12k
所以k
2k,k2
3+4k2
6-8k2
3+4x-2-4k
所以kk2
4k2
如图,已知椭圆C的方程:x+y2=1,4、4、B、B2是椭圆C的顶点,P
是椭圆C上除顶点外的任意点,直线BP交x轴于点F,直线AB2交A1P于点E.设
AP的斜率为k,EF的斜率为m,求证:2m-k为定值
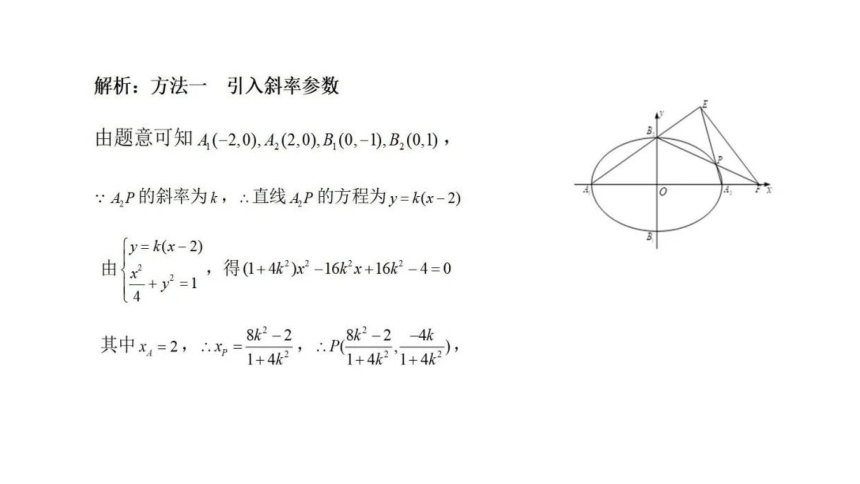
解析:方法一引入斜率参数
由题意可知4(-2,0),41(2,0),B1(0,-1,B20.),
A1P的斜率为k,∴直线A2P的方程为y=k(x-2)
由
,得(1+4k2)x2-16k2x+16k2-4=0
+y2=1
其中x1=2,
1+4k
1+4k21+4k
椭圆中有关定值问题
单击输入您的封面副标题
二、经典例题
方法二 引入斜率参数法
变式拓展
方法一 引入点参数
方法二 引入斜率参数法
练习:
方法总结
背景介绍
解析几何″因其运算繁难,“要想高考好、解几很重要”,自然成为我们备
战高考的重点,而椭圆中的定值问题又是解析几何命题的热点,2012年江
苏卷,2018年全国卷都作为难题出现。“动中求定”,因其“动”,这类问题
中的变量较多变量间的关系式也复杂,对我们分析能力、运算能力都有比
较高的要求。但是,如果我们透视定值问题的本质,解决的通法是“引参制
动〃,即引入适切的变量,把要求的量用它表示出来,再探索其“定〃的特质
例1.如图,在平面直角坐标系xOy中,椭圆
1,若点A,B分别是椭圆的
左、右顶点,直线1经过点B且垂直于x轴,点P是椭圆上异于A,B的任意一点,
直线AP交1于点M,若直线OM的斜率为k1,直线BP的斜率为k2,求证:kk2
为定值
方法一引入点参数
详解:设P(x,y)(y1≠0),M(2y3),则k=2,k2=-当
x
AP,M三点共线,所以y
4
y1
X,-+
所以起2=-J0y14y
2(x-2)2(x2-4)
因为点P(x,y1)在椭圆上,所以4y2=3(4-x
故kk2
4
为定值
(x2-4)2
详解:由题意知直线AP的斜率存在且不为零,设直线AP:y=k(x+2)
M
y=k(x+2)
由
,消去y得(3+4k2)x2+16k2x+16k2-12
又x4=-2,所以x
6-8k212k
3+4k
3+4k2°3+4k2
在直线中令x=2得yx=4k,∴M(2,4k)
12k
所以k
2k,k2
3+4k2
6-8k2
3+4x-2-4k
所以kk2
4k2
如图,已知椭圆C的方程:x+y2=1,4、4、B、B2是椭圆C的顶点,P
是椭圆C上除顶点外的任意点,直线BP交x轴于点F,直线AB2交A1P于点E.设
AP的斜率为k,EF的斜率为m,求证:2m-k为定值
解析:方法一引入斜率参数
由题意可知4(-2,0),41(2,0),B1(0,-1,B20.),
A1P的斜率为k,∴直线A2P的方程为y=k(x-2)
由
,得(1+4k2)x2-16k2x+16k2-4=0
+y2=1
其中x1=2,
1+4k
1+4k21+4k
同课章节目录
