2021-2022学年北师大版九年级数学下册第二章二次函数单元检测试卷(Word版,附答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册第二章二次函数单元检测试卷(Word版,附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 96.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-04 14:37:48 | ||
图片预览



文档简介
第二章 二 次 函 数 检测
一、选择题(本大题10小题,每小题3分,共30分)
1. 下列函数为二次函数的是( )
A. y=-4x+5 B. y=x(2x-3) C. y=(x+4)2-x2 D. y=
2. 将抛物线y=(x-1)2+4先向右平移4个单位长度,再向下平移3个单位长度,得到的抛物线的顶点坐标为( )
A. (5,4) B. (1,4) C. (1,1) D. (5,1)
3. 二次函数y=x2+2x-7的函数值是8,那么对应的x的值是( )
A. 3 B. 5 C. -3和5 D. 3和-5
4. 已知二次函数y=ax2+bx+c(a≠0)的图象如图X2-1所示,并且关于x的一元二次方程ax2+bx+c-m=0有两个不相等的实数根,下列结论:①b2-4ac<0;②abc>0;③a-b+c<0;④m>-2.其中正确的有( )
图X2-1
A. 1个 B. 2个 C. 3个 D. 4个
5. 已知函数y=x2-x-4,当函数值y随x的增大而减小时,x的取值范围是( )
A. x<1 B. x>1 C. x>-2 D. -2<x<4
6. 已知二次函数y=3(x-1)2+k的图象上有A(,y1),B(2,y2),C(-,y3)三个点,则y1,y2,y3的大小关系是( )
A. y1>y2>y3 B. y2>y1>y3
C. y3>y1>y2 D. y3>y2>y1
7. 若抛物线y=x2+8x-k的顶点在x轴上,则k的值为( )
A. -16 B. 16 C. -8 D. 8
8. 对于抛物线y=-(x+1)2+3,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>1时,y随x的增大而减小. 其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
9. 已知函数y=ax和y=a(x+m)2+n,且a>0,m<0,n<0,则这两个函数图象在同一坐标系内的大致图象是( )
10. 抛物线y=x2-2x-3与x轴交于点A,B(A在左,B在右),与y轴交于点C,下列结论正确的是( )
A. AB=3 B. 对称轴为直线x=2
C. 函数最大值为-4 D. cos∠ABC=
二、填空题(本大题7小题,每小题4分,共28分)
11. 若抛物线y=ax2+bx+c经过点(-1,10),则a-b+c= .
12. 已知抛物线y=-x2-2x+m 的顶点在x轴上方,则 .
13. 如图X2-2,直线y=mx+n与抛物线y=ax2+bx+c交于A(-1,p),B(4,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是 .
图X2-2
14. 将二次函数y=(x-2)2+3的图象向右平移2个单位长度,再向下平移2个单位长度,所得二次函数的解析式为 .
15. 已知关于x的方程x2-4x+3-a=0在0<x<4范围内有两个根,则a的取值范围是 .
16. 当-2≤x≤1时,二次函数y=-(x-m)2+m2+1有最大值4,则实数m的值是 .
17. 教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-(x-4)2+3,由此可知铅球推出的距离是 m.
三、解答题(一)(本大题3小题,每小题6分,共18分)
18. 已知y=(m2-m)xm2-2m-1+(m-3)x+m2是关于x的二次函数,求m的值和二次函数的解析式.
19. 若二次函数y=x2+mx的图象的对称轴是直线x=3,求关于x的方程x2+mx=7的解.
20. 已知抛物线y=x2+x-.
(1)用配方法求出它的顶点坐标和对称轴;
(2)若抛物线与x轴的两个交点为A,B,求线段AB的长.
.
四、解答题 (二)(本大题3小题,每小题8分,共24分)
21. 如图X2-3,抛物线y=x2-bx+c交x轴于点A(1,0)和点C,交y轴于点B,对称轴是直线x=2.
(1)求抛物线的解析式;
(2)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
图X2-3
22. 已知:二次函数y=x2-4x+3a+2(a为常数).
(1)请写出该二次函数的三条性质;
(2)在同一直角坐标系中,若该二次函数的图象在x≤4的部分与一次函数y=2x-1的图象有两个交点,求a的取值范围.
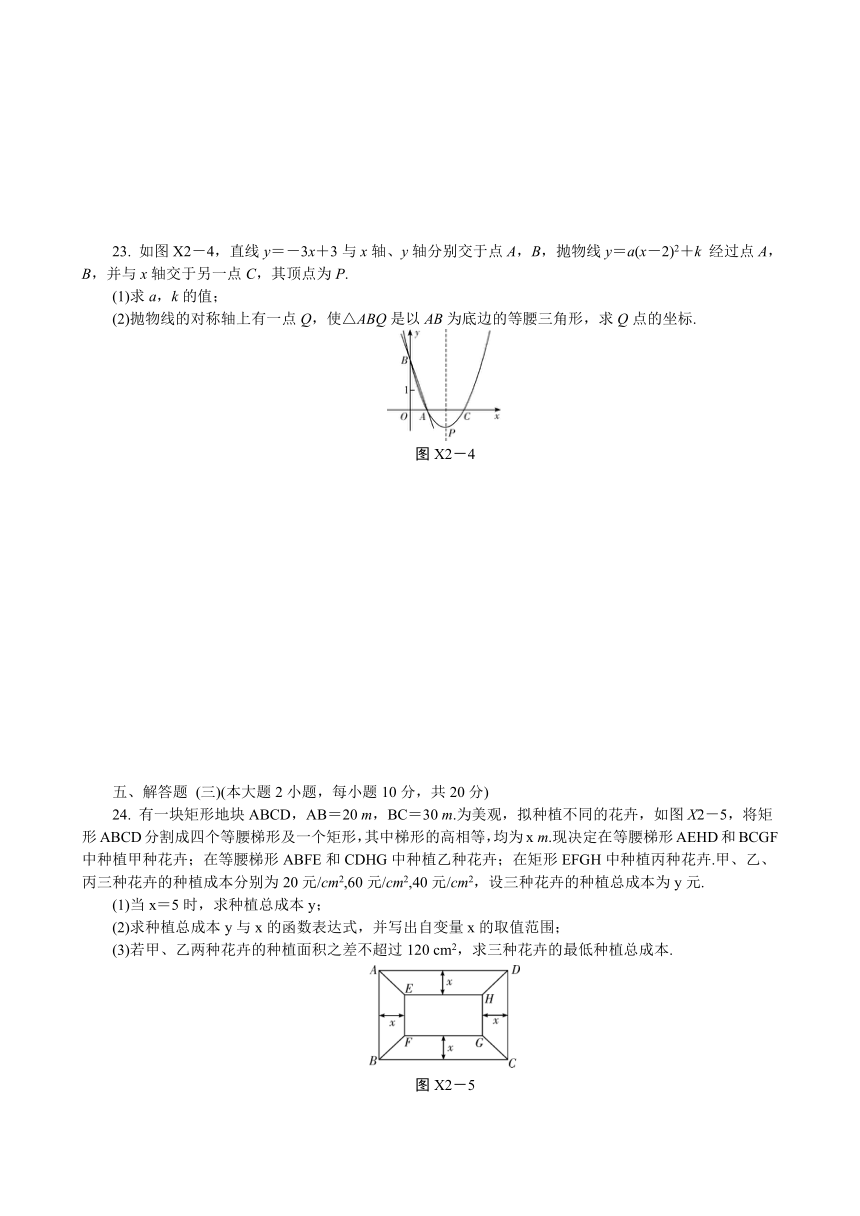
23. 如图X2-4,直线y=-3x+3与x轴、y轴分别交于点A,B,抛物线y=a(x-2)2+k 经过点A,B,并与x轴交于另一点C,其顶点为P.
(1)求a,k的值;
(2)抛物线的对称轴上有一点Q,使△ABQ是以AB为底边的等腰三角形,求Q点的坐标.
图X2-4
五、解答题 (三)(本大题2小题,每小题10分,共20分)
24. 有一块矩形地块ABCD,AB=20 m,BC=30 m.为美观,拟种植不同的花卉,如图X2-5,将矩形ABCD分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为x m.现决定在等腰梯形AEHD和BCGF中种植甲种花卉;在等腰梯形ABFE和CDHG中种植乙种花卉;在矩形EFGH中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元/cm2,60元/cm2,40元/cm2,设三种花卉的种植总成本为y元.
(1)当x=5时,求种植总成本y;
(2)求种植总成本y与x的函数表达式,并写出自变量x的取值范围;
(3)若甲、乙两种花卉的种植面积之差不超过120 cm2,求三种花卉的最低种植总成本.
图X2-5
25. 在平面直角坐标系中,已知抛物线C:y=ax2+2x-1(a≠0)和直线l:y=kx+b,点A(-3,-3),B(1,-1)均在直线l上.
(1)若抛物线C与直线l有交点,求a的取值范围;
(2)当a=-1,二次函数y=ax2+2x-1的自变量x满足m≤x≤m+2时,函数y的最大值为-4,求m的值.
答案
1. B 2. D 3. D 4. B 5. A 6. D 7. A 8. C 9. B 10. D 11. 10 12. m>-1 13. x<-1或x>4
14. y=(x-4)2+1 15. -1≤a<3
16. 2或- 17. 10
18. 解:∵y=(m2-m)xm2-2m-1+(m-3)x+m2是关于x的二次函数,
∴
解得m=3或m=-1.
∴此二次函数的解析式为y=6x2+9或y=2x2-4x+1.
19. 解:∵二次函数y=x2+mx的图象的对称轴是直线x=3,
∴-=3,解得m=-6.
∴关于x的方程x2+mx=7可化为x2-6x-7=0,
即(x+1)(x-7)=0.
解得x1=-1,x2=7.
20. 解:(1)∵y= x2+x-=(x+1)2-3,
∴抛物线的顶点坐标为(-1,-3),对称轴是直线x=-1.
(2)当y=0时, x2+x-=0,
解得x1=-1+,x2=-1-.
∴AB==2.
21. 解:(1)由题意,得
解得
∴抛物线的解析式为y=x2-4x+3.
(2)∵点A与点C关于直线x=2对称,
∴连接BC,与直线x=2交于点P,如答图X2-1,则点P即为所求.
答图X2-1
根据抛物线的对称性可知,点C的坐标为(3,0),y=x2-4x+3与y轴的交点为B(0,3),
∴设直线BC的解析式为y=kx+b1,则有 解得
∴直线BC的解析式为y=-x+3.
则直线BC与直线x=2的交点坐标为(2,1).
∴点P的坐标为(2,1).
22. 解:(1)∵二次函数y=x2-4x+3a+2=(x-2)2+3a-2.
∴该二次函数的图象开口向上,对称轴为直线x=2,顶点坐标为(2,3a-2).
其性质有:①开口向上;②有最小值3a-2;③对称轴为直线x=2.
(2)∵二次函数的图象在x≤4的部分与一次函数y=2x-1的图象有两个交点,
∴x2-4x+3a+2=2x-1.整理,得x2-6x+3a+3=0.
∴Δ=36-4(3a+3)>0.解得a<2.
把x=4代入y=2x-1,解得y=2×4-1=7.
把(4,7)代入y=x2-4x+3a+2,得7=16-16+3a+2.解得a=.
∴若该二次函数的图象在x≤4的部分与一次函数y=2x-1的图象有两个交点,a的取值范围为≤a<2.
23. 解:(1)∵直线y=-3x+3与x轴、y轴分别交于点A,B,
∴A(1,0),B(0,3).
又∵抛物线y=a(x-2)2+k经过点A(1,0),B(0,3),
∴解得
∴a,k的值分别为1,-1.
(2)设Q点的坐标为(2,m),对称轴直线x=2交x轴于点F,过点B作BE垂直直线x=2于点E,如答图X2-2.
答图X2-2
在Rt△AQF中,AQ2=AF2+QF2=1+m2,
在Rt△BQE中,BQ2=BE2+EQ2=4+(3-m)2.
∵AQ=BQ,∴1+m2=4+(3-m)2.
∴m=2.
∴Q点的坐标为(2,2).
24. 解:(1)当x=5时,EF=20-2x=10,EH=30-2x=20,
∴y=2×(EH+AD)×20x+2×(GH+CD)×60x+EH·EF×40=(20+30)×5×20+(10+20)×5×60+20×10×40=22 000.
(2)由题意,得EF=20-2x,EH=30-2x,
y=2×(30-2x+30)·x·20+2×(20-2x+20)·x·60+(30-2x)(20-2x)·40=-400x+24 000(0<x<10).
(3)S甲=2×(EH+AD)x=(30-2x+30)x=-2x2+60x,
同理可得S乙=-2x2+40x.
∵甲、乙两种花卉的种植面积之差不超过120 cm2,
∴-2x2+60x-(-2x2+40x)≤120.
解得x≤6.
∴0<x≤6.
∵y=-400x+24 000随x的增大而减小,
∴当x=6时,y取得最小值,
y最小=-400×6+24 000=21 600,
答:三种花卉的最低种植总成本为21 600元.
25. 解:(1)将点A(-3,-3),B(1,-1)代入y=kx+b,得
∴
∴直线l的解析式为y=x-.
联立y=ax2+2x-1与y=x-,则有2ax2+3x+1=0.
∵抛物线C与直线l有交点,
∴Δ=9-8a≥0.
∴a≤且a≠0.
(2)根据题意,得y=-x2+2x-1.
∵a<0,∴抛物线开口向下,对称轴为直线x=1.
∵m≤x≤m+2时,y有最大值-4,
∴当y=-4时,-x2+2x-1=-4.
解得x=-1或x=3.
①在对称轴直线x=1的左侧,y随x的增大而增大,
∴x=m+2=-1时,即m=-3.y有最大值-4.
②在对称轴直线x=1的右侧,y随x的增大而减小,
∴x=m=3时,y有最大值-4.
综上所述,m=-3或m=3.
一、选择题(本大题10小题,每小题3分,共30分)
1. 下列函数为二次函数的是( )
A. y=-4x+5 B. y=x(2x-3) C. y=(x+4)2-x2 D. y=
2. 将抛物线y=(x-1)2+4先向右平移4个单位长度,再向下平移3个单位长度,得到的抛物线的顶点坐标为( )
A. (5,4) B. (1,4) C. (1,1) D. (5,1)
3. 二次函数y=x2+2x-7的函数值是8,那么对应的x的值是( )
A. 3 B. 5 C. -3和5 D. 3和-5
4. 已知二次函数y=ax2+bx+c(a≠0)的图象如图X2-1所示,并且关于x的一元二次方程ax2+bx+c-m=0有两个不相等的实数根,下列结论:①b2-4ac<0;②abc>0;③a-b+c<0;④m>-2.其中正确的有( )
图X2-1
A. 1个 B. 2个 C. 3个 D. 4个
5. 已知函数y=x2-x-4,当函数值y随x的增大而减小时,x的取值范围是( )
A. x<1 B. x>1 C. x>-2 D. -2<x<4
6. 已知二次函数y=3(x-1)2+k的图象上有A(,y1),B(2,y2),C(-,y3)三个点,则y1,y2,y3的大小关系是( )
A. y1>y2>y3 B. y2>y1>y3
C. y3>y1>y2 D. y3>y2>y1
7. 若抛物线y=x2+8x-k的顶点在x轴上,则k的值为( )
A. -16 B. 16 C. -8 D. 8
8. 对于抛物线y=-(x+1)2+3,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>1时,y随x的增大而减小. 其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
9. 已知函数y=ax和y=a(x+m)2+n,且a>0,m<0,n<0,则这两个函数图象在同一坐标系内的大致图象是( )
10. 抛物线y=x2-2x-3与x轴交于点A,B(A在左,B在右),与y轴交于点C,下列结论正确的是( )
A. AB=3 B. 对称轴为直线x=2
C. 函数最大值为-4 D. cos∠ABC=
二、填空题(本大题7小题,每小题4分,共28分)
11. 若抛物线y=ax2+bx+c经过点(-1,10),则a-b+c= .
12. 已知抛物线y=-x2-2x+m 的顶点在x轴上方,则 .
13. 如图X2-2,直线y=mx+n与抛物线y=ax2+bx+c交于A(-1,p),B(4,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是 .
图X2-2
14. 将二次函数y=(x-2)2+3的图象向右平移2个单位长度,再向下平移2个单位长度,所得二次函数的解析式为 .
15. 已知关于x的方程x2-4x+3-a=0在0<x<4范围内有两个根,则a的取值范围是 .
16. 当-2≤x≤1时,二次函数y=-(x-m)2+m2+1有最大值4,则实数m的值是 .
17. 教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-(x-4)2+3,由此可知铅球推出的距离是 m.
三、解答题(一)(本大题3小题,每小题6分,共18分)
18. 已知y=(m2-m)xm2-2m-1+(m-3)x+m2是关于x的二次函数,求m的值和二次函数的解析式.
19. 若二次函数y=x2+mx的图象的对称轴是直线x=3,求关于x的方程x2+mx=7的解.
20. 已知抛物线y=x2+x-.
(1)用配方法求出它的顶点坐标和对称轴;
(2)若抛物线与x轴的两个交点为A,B,求线段AB的长.
.
四、解答题 (二)(本大题3小题,每小题8分,共24分)
21. 如图X2-3,抛物线y=x2-bx+c交x轴于点A(1,0)和点C,交y轴于点B,对称轴是直线x=2.
(1)求抛物线的解析式;
(2)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
图X2-3
22. 已知:二次函数y=x2-4x+3a+2(a为常数).
(1)请写出该二次函数的三条性质;
(2)在同一直角坐标系中,若该二次函数的图象在x≤4的部分与一次函数y=2x-1的图象有两个交点,求a的取值范围.
23. 如图X2-4,直线y=-3x+3与x轴、y轴分别交于点A,B,抛物线y=a(x-2)2+k 经过点A,B,并与x轴交于另一点C,其顶点为P.
(1)求a,k的值;
(2)抛物线的对称轴上有一点Q,使△ABQ是以AB为底边的等腰三角形,求Q点的坐标.
图X2-4
五、解答题 (三)(本大题2小题,每小题10分,共20分)
24. 有一块矩形地块ABCD,AB=20 m,BC=30 m.为美观,拟种植不同的花卉,如图X2-5,将矩形ABCD分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为x m.现决定在等腰梯形AEHD和BCGF中种植甲种花卉;在等腰梯形ABFE和CDHG中种植乙种花卉;在矩形EFGH中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元/cm2,60元/cm2,40元/cm2,设三种花卉的种植总成本为y元.
(1)当x=5时,求种植总成本y;
(2)求种植总成本y与x的函数表达式,并写出自变量x的取值范围;
(3)若甲、乙两种花卉的种植面积之差不超过120 cm2,求三种花卉的最低种植总成本.
图X2-5
25. 在平面直角坐标系中,已知抛物线C:y=ax2+2x-1(a≠0)和直线l:y=kx+b,点A(-3,-3),B(1,-1)均在直线l上.
(1)若抛物线C与直线l有交点,求a的取值范围;
(2)当a=-1,二次函数y=ax2+2x-1的自变量x满足m≤x≤m+2时,函数y的最大值为-4,求m的值.
答案
1. B 2. D 3. D 4. B 5. A 6. D 7. A 8. C 9. B 10. D 11. 10 12. m>-1 13. x<-1或x>4
14. y=(x-4)2+1 15. -1≤a<3
16. 2或- 17. 10
18. 解:∵y=(m2-m)xm2-2m-1+(m-3)x+m2是关于x的二次函数,
∴
解得m=3或m=-1.
∴此二次函数的解析式为y=6x2+9或y=2x2-4x+1.
19. 解:∵二次函数y=x2+mx的图象的对称轴是直线x=3,
∴-=3,解得m=-6.
∴关于x的方程x2+mx=7可化为x2-6x-7=0,
即(x+1)(x-7)=0.
解得x1=-1,x2=7.
20. 解:(1)∵y= x2+x-=(x+1)2-3,
∴抛物线的顶点坐标为(-1,-3),对称轴是直线x=-1.
(2)当y=0时, x2+x-=0,
解得x1=-1+,x2=-1-.
∴AB==2.
21. 解:(1)由题意,得
解得
∴抛物线的解析式为y=x2-4x+3.
(2)∵点A与点C关于直线x=2对称,
∴连接BC,与直线x=2交于点P,如答图X2-1,则点P即为所求.
答图X2-1
根据抛物线的对称性可知,点C的坐标为(3,0),y=x2-4x+3与y轴的交点为B(0,3),
∴设直线BC的解析式为y=kx+b1,则有 解得
∴直线BC的解析式为y=-x+3.
则直线BC与直线x=2的交点坐标为(2,1).
∴点P的坐标为(2,1).
22. 解:(1)∵二次函数y=x2-4x+3a+2=(x-2)2+3a-2.
∴该二次函数的图象开口向上,对称轴为直线x=2,顶点坐标为(2,3a-2).
其性质有:①开口向上;②有最小值3a-2;③对称轴为直线x=2.
(2)∵二次函数的图象在x≤4的部分与一次函数y=2x-1的图象有两个交点,
∴x2-4x+3a+2=2x-1.整理,得x2-6x+3a+3=0.
∴Δ=36-4(3a+3)>0.解得a<2.
把x=4代入y=2x-1,解得y=2×4-1=7.
把(4,7)代入y=x2-4x+3a+2,得7=16-16+3a+2.解得a=.
∴若该二次函数的图象在x≤4的部分与一次函数y=2x-1的图象有两个交点,a的取值范围为≤a<2.
23. 解:(1)∵直线y=-3x+3与x轴、y轴分别交于点A,B,
∴A(1,0),B(0,3).
又∵抛物线y=a(x-2)2+k经过点A(1,0),B(0,3),
∴解得
∴a,k的值分别为1,-1.
(2)设Q点的坐标为(2,m),对称轴直线x=2交x轴于点F,过点B作BE垂直直线x=2于点E,如答图X2-2.
答图X2-2
在Rt△AQF中,AQ2=AF2+QF2=1+m2,
在Rt△BQE中,BQ2=BE2+EQ2=4+(3-m)2.
∵AQ=BQ,∴1+m2=4+(3-m)2.
∴m=2.
∴Q点的坐标为(2,2).
24. 解:(1)当x=5时,EF=20-2x=10,EH=30-2x=20,
∴y=2×(EH+AD)×20x+2×(GH+CD)×60x+EH·EF×40=(20+30)×5×20+(10+20)×5×60+20×10×40=22 000.
(2)由题意,得EF=20-2x,EH=30-2x,
y=2×(30-2x+30)·x·20+2×(20-2x+20)·x·60+(30-2x)(20-2x)·40=-400x+24 000(0<x<10).
(3)S甲=2×(EH+AD)x=(30-2x+30)x=-2x2+60x,
同理可得S乙=-2x2+40x.
∵甲、乙两种花卉的种植面积之差不超过120 cm2,
∴-2x2+60x-(-2x2+40x)≤120.
解得x≤6.
∴0<x≤6.
∵y=-400x+24 000随x的增大而减小,
∴当x=6时,y取得最小值,
y最小=-400×6+24 000=21 600,
答:三种花卉的最低种植总成本为21 600元.
25. 解:(1)将点A(-3,-3),B(1,-1)代入y=kx+b,得
∴
∴直线l的解析式为y=x-.
联立y=ax2+2x-1与y=x-,则有2ax2+3x+1=0.
∵抛物线C与直线l有交点,
∴Δ=9-8a≥0.
∴a≤且a≠0.
(2)根据题意,得y=-x2+2x-1.
∵a<0,∴抛物线开口向下,对称轴为直线x=1.
∵m≤x≤m+2时,y有最大值-4,
∴当y=-4时,-x2+2x-1=-4.
解得x=-1或x=3.
①在对称轴直线x=1的左侧,y随x的增大而增大,
∴x=m+2=-1时,即m=-3.y有最大值-4.
②在对称轴直线x=1的右侧,y随x的增大而减小,
∴x=m=3时,y有最大值-4.
综上所述,m=-3或m=3.
