第二章 二次函数综合问题“五大题型”专项训练(含解析)
文档属性
| 名称 | 第二章 二次函数综合问题“五大题型”专项训练(含解析) | 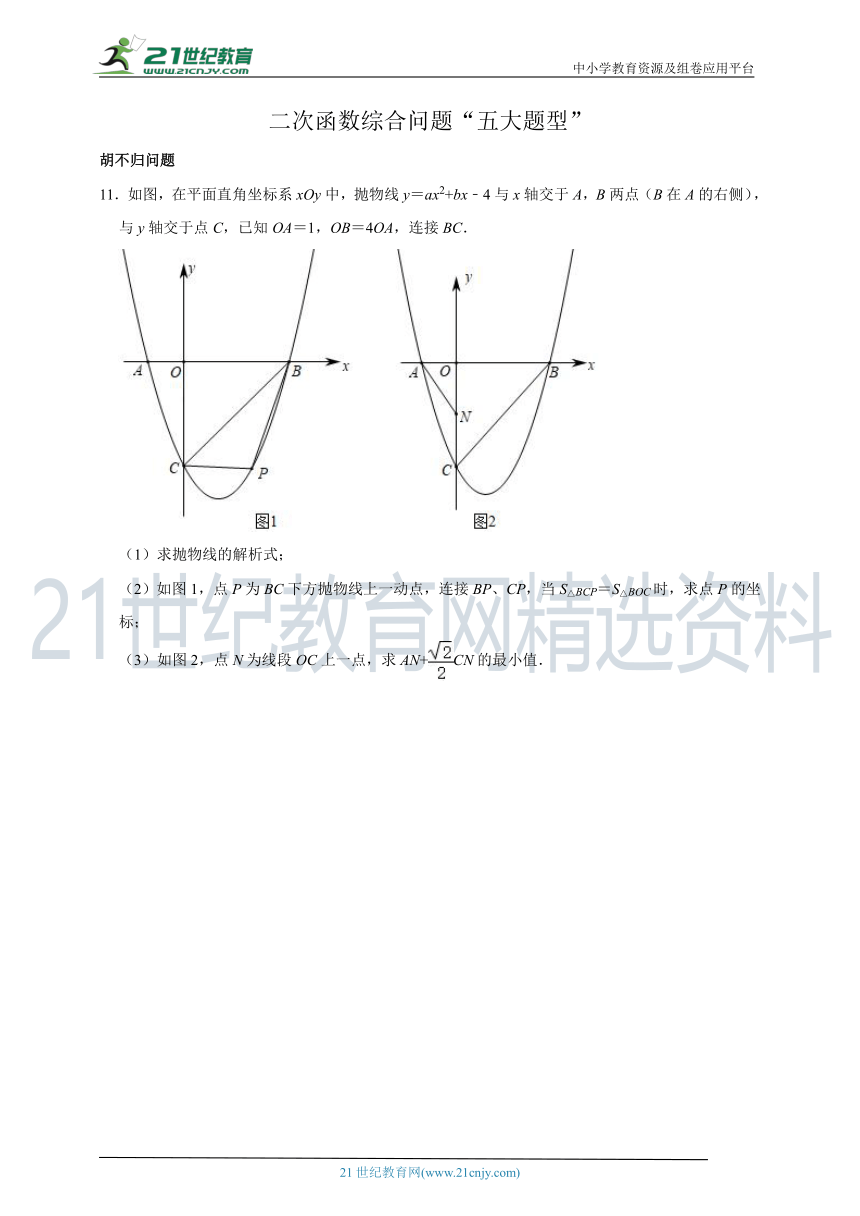 | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-06 19:52:38 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
二次函数综合问题“五大题型”
胡不归问题
11.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣4与x轴交于A,B两点(B在A的右侧),与y轴交于点C,已知OA=1,OB=4OA,连接BC.
(1)求抛物线的解析式;
(2)如图1,点P为BC下方抛物线上一动点,连接BP、CP,当S△BCP=S△BOC时,求点P的坐标;
(3)如图2,点N为线段OC上一点,求AN+CN的最小值.
相似问题
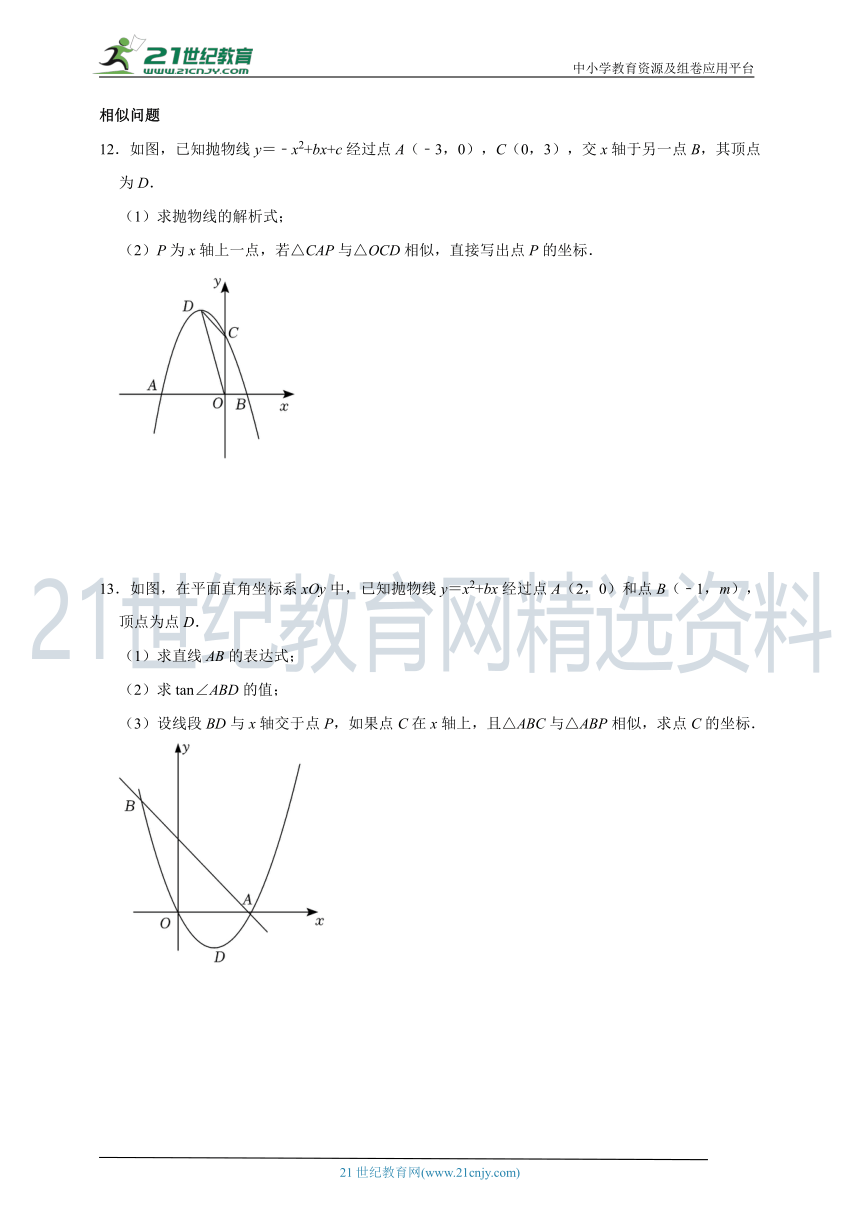
12.如图,已知抛物线y=﹣x2+bx+c经过点A(﹣3,0),C(0,3),交x轴于另一点B,其顶点为D.
(1)求抛物线的解析式;
(2)P为x轴上一点,若△CAP与△OCD相似,直接写出点P的坐标.
13.如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx经过点A(2,0)和点B(﹣1,m),顶点为点D.
(1)求直线AB的表达式;
(2)求tan∠ABD的值;
(3)设线段BD与x轴交于点P,如果点C在x轴上,且△ABC与△ABP相似,求点C的坐标.
平行四边形问题
14.如图,已知抛物线y=x2+bx+c的对称轴为直线x=4,与y轴相交于点B(0,﹣5).
(1)求抛物线的函数解析式;
(2)求直线AB的解析式并直接写出线段AB的中点M的坐标;
(3)设动点P,Q分别在抛物线和对称轴l上,当以A,P,Q,M为顶点的四边形是平行四边形时,直接写出Q点的坐标.
直角三角形问题
15.如图,直线y=x+b和抛物线y=ax2﹣x+2都经过A(0,n)和B(m,4)两点,抛物线y=ax2﹣x+2与x轴交于C、D两点(点C在点D右侧).
(1)求直线和抛物线的函数表达式;
(2)求四边形ABCD的面积S;
(3)在x轴上是否存在点P,使得△PAB是以AP为直角边的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.
等腰三角形问题
16.如图,在平面直角坐标系中,已知抛物线y=x2+bx+c与直线AB相交于A,B两点,其中A(﹣3,﹣4),B(0,﹣1).
(1)求该抛物线的函数表达式.
(2)点P为直线AB下方抛物线上的任意一点,连接PA,PB,求△PAB面积的最大值.
(3)在二次函数的对称轴上找一点C,使得△ABC是等腰三角形,求满足条件的点C的坐标.
练习题(作业)
17.在平面直角坐标系中,过点A(3,4)的抛物线y=ax2+bx+4与x轴交于点B(﹣1,0),与y轴交于点C,过点A作AD⊥x轴于点D.
(1)求抛物线的解析式.
(2)如图1,点P是直线AB上方抛物线上的一个动点,连接PD交AB于点Q,连接AP,当S△AQD=2S△APQ时,求点P的坐标.
(3)如图2,点G是线段OC上一个动点,连结DG,求DG+CG的最小值.
参考答案与试题解析
11.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣4与x轴交于A,B两点(B在A的右侧),与y轴交于点C,已知OA=1,OB=4OA,连接BC.
(1)求抛物线的解析式;
(2)如图1,点P为BC下方抛物线上一动点,连接BP、CP,当S△BCP=S△BOC时,求点P的坐标;
(3)如图2,点N为线段OC上一点,求AN+CN的最小值.
【解答】解:(1)∵OA=1,OB=4OA,
∴OB=4,
∴A(﹣1,0),B(4,0),
将A,B坐标代入抛物线解析式得,,
解得,
∴抛物线的解析式为:y=x2﹣3x﹣4;
(2)过点P作y轴的平行线,交BC于点Q,
设点P的横坐标为t,则P(t,t2﹣3t﹣4),
由(1)知抛物线的解析式为y=x2﹣3x﹣4,
令x=0,则y=﹣4,
∴C(0,﹣4),
∴OB=OC=4,
∴S△BOC=×4×4=8.
设直线BC的解析式为y=mx+n,
则,解得,
∴直线MN的解析式为y=x﹣4,
∴Q(t,t﹣4),
∴QP=t﹣4﹣(t2﹣3t﹣4)=﹣t2+4t,
∴S△BCP=S△BCP+S△BCP=PQ (xB﹣xQ)+PQ (xQ﹣xC)=PQ (xB﹣xC)= (﹣t2+4t)×(4﹣0)=﹣2t2+8t,
∵S△BCP=S△BOC,
∴﹣2t2+8t=8,
解得t=2;
此时y=22﹣3×2﹣4=﹣6,
∴P(2,﹣6);
(3)如图,过点N作NM⊥BC于点M,
∴∠CMN=90°,
由(2)知,OB=OC=4,
∴∠OBC=∠OCB=45°,
∴△CNM是等腰直角三角形,
∴NM=CN,
∴AN+CN=AN+NM,
则当A,N,M三点共线时,即AM⊥BC时,取到最小值,如图,过点A作AM′⊥BC于点M′,
则△AM′B是等腰直角三角形,
∴AM′=AB=.
∴AN+CN的最小值为:.
12.如图,已知抛物线y=﹣x2+bx+c经过点A(﹣3,0),C(0,3),交x轴于另一点B,其顶点为D.
(1)求抛物线的解析式;
(2)P为x轴上一点,若△CAP与△OCD相似,直接写出点P的坐标.
【解答】解:(1)把A(﹣3,0),C(0,3)代入抛物线解析式,,
解得,
∴抛物线的解析式为:y=﹣x2﹣2x+3;
(2)由(1)知,y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴点D(﹣1,4),
如图,过点D作DE⊥y轴于点E,
则DE=1,OE=4,
∵OC=3,
∴CE=1,
∴DE=CE,
∴∠DCE=45°,CD=,
∴∠OCD=135°,CD:OC=:3;
∵A(﹣3,0),C(0,3),
∴OA=OC=3,
∴∠OAC=∠OCA=45°,AC=3,
若△CAP与△OCD相似,点P只能在点A的左侧,
此时∠PAC=135°,且AP:AC=CD:OC或AP:AC=OC:CD,
∴AP:3=:3,或AP:3=3:,
解得AP=2或AP=9,
即P(﹣5,0)或P(﹣12,0).
13.如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx经过点A(2,0)和点B(﹣1,m),顶点为点D.
(1)求直线AB的表达式;
(2)求tan∠ABD的值;
(3)设线段BD与x轴交于点P,如果点C在x轴上,且△ABC与△ABP相似,求点C的坐标.
【解答】解:(1)将A(2,0)代入y=x2+bx,
∴4+2b=0,
∴b=﹣2,
∴y=x2﹣2x,
将B(﹣1,m)代入y=x2﹣2x,
∴m=3,
∴B(﹣1,3),
设直线AB的解析式为y=kx+b,
∴,
∴,
∴y=﹣x+2;
(2)∵y=x2﹣2x=(x﹣1)2﹣1,
∴D(1,﹣1),
∴AD=,AB=2,BC=3,
∵AB2=AD2+BC2,
∴△ABD是直角三角形,
∴tan∠ABD==;
(3)设直线BD的解析式为y=k1x+b1,
∴,
∴,
∴y=﹣2x+1,
令y=0,则x=,
∴P(,0),
设C(t,0),
如图1,当∠ABC=∠APB时,△ABP∽△APC,
∴∠ACB=∠ABP,
过B点作BQ⊥x轴交于点Q,
∴tan∠BCQ==,
∴CQ=9,
∴CO=10,
∴C(﹣10,0);
如图2,当∠PBC=∠BAP时,△ABP∽△BCP,
∴∠ABP=∠BCP,
过B点作BQ⊥x轴交于点Q,
∴tan∠BCP===,
∴CG=9,
∴OC=8,
∴C(8,0);
综上所述:C点的坐标为(﹣10,0)或(8,0).
14.如图,已知抛物线y=x2+bx+c的对称轴为直线x=4,与y轴相交于点B(0,﹣5).
(1)求抛物线的函数解析式;
(2)求直线AB的解析式并直接写出线段AB的中点M的坐标;
(3)设动点P,Q分别在抛物线和对称轴l上,当以A,P,Q,M为顶点的四边形是平行四边形时,直接写出Q点的坐标.
【解答】解:(1)根据题意可知,x=﹣=4,a=﹣,解得b=4;
将点B(0,﹣5)代入抛物线解析式可得c=﹣5,
∴抛物线的表达式为:y=﹣x2+4x﹣5;
(2)∵y=﹣x2+4x﹣5=﹣(x﹣4)2+3,
∴A(4,3),B(0,﹣5),
∴点M(2,﹣1),
设直线AB的表达式为:y=kx﹣5,
将点A坐标代入上式得:3=4k﹣5,解得:k=2,
∴直线AB的表达式为:y=2x﹣5;
(3)设点Q(4,s)、点P(m,﹣m2+4m﹣5),
①当AM是平行四边形的一条边时,
当点Q在A的下方时,
点A向左平移2个单位、向下平移4个单位得到M,
同样点P(m,﹣m2+4m﹣5)向左平移2个单位、向下平移4个单位得到Q(4,s),
即:m﹣2=4,﹣m2+4m﹣5﹣4=s,
解得:m=6,s=﹣3,
∴点Q的坐标为(4,﹣3),
故当点Q在点A上方时,AQ=MP=2,
同理可得点Q的坐标为(4,5),
②当AM是平行四边形的对角线时,
由中点定理得:4+2=m+4,3﹣1=﹣m2+4m﹣5+s,
解得:m=2,s=1,
∴Q的坐标分别为(4,1);
综上,Q的坐标分别为Q(4,﹣3)或(4,1)或(4,5).
15.如图,直线y=x+b和抛物线y=ax2﹣x+2都经过A(0,n)和B(m,4)两点,抛物线y=ax2﹣x+2与x轴交于C、D两点(点C在点D右侧).
(1)求直线和抛物线的函数表达式;
(2)求四边形ABCD的面积S;
(3)在x轴上是否存在点P,使得△PAB是以AP为直角边的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.
【解答】解:(1)把(0,n)代入y=ax2﹣x+2中得,
n=2,即A(0,2),
把(0,2)代入y=x+b中得,
b=2,
∴y=x+2,
把B(m,4)代入y=x+2中得,
+2=4,
∴m=6,即B(6,4),
把B(6,4)代入y=ax2﹣x+2中得,36a﹣10+2=4,
∴a=,即y=x2﹣x+2,
∴直线表达式是y=x+2,
抛物线解析式为:y=x2﹣x+2;
(2)解方程x2﹣x+2=0,得
x1=2,x2=3,
∵点C在点D右侧,
∴C(3,0),D(2,0),
过B作BE⊥y轴于E,作BF⊥x轴于F,
∴E(6,0),
∵A(0,2),B(6,4),C(3,0),D(2,0),
∴AO=2,DO=2,CE=3,BE=4,OE=6,
∴S四边形ABCD=S梯形ABCD﹣S△AOD﹣S△BCE
=(AO+BE) OE﹣AO OD﹣BE CE
=×(2+4)×6﹣×2×2﹣×3×4
=18﹣2﹣6
=10,即四边形ABCD的面积为10;
(3)设P(t,0),A(0,2),B(6,4),
∴PA2=t2+4,BP2=(t﹣6)2+16,
AB2=36+4=40,
①当∠PAB=90°时,
∴t2+4+40=(t﹣6)2+16,
∴t=,即P(,0);
②当∠APB=90°时,
∴t2+4+(t﹣6)2+16+40,
∴x=2或4,
∴P(2,0)或P(4,0),
综上所述△PAB以AP为直角边时,P(,0)或P(2,0)或P(4,0).
16.如图,在平面直角坐标系中,已知抛物线y=x2+bx+c与直线AB相交于A,B两点,其中A(﹣3,﹣4),B(0,﹣1).
(1)求该抛物线的函数表达式.
(2)点P为直线AB下方抛物线上的任意一点,连接PA,PB,求△PAB面积的最大值.
(3)在二次函数的对称轴上找一点C,使得△ABC是等腰三角形,求满足条件的点C的坐标.
【解答】解:(1)将A(﹣3,﹣4),B(0,﹣1)代入y=x2+bx+c,
得,
解得,
∴y=x2+4x﹣1;
(2)设直线AB的解析式为y=kx+b,
则,
解得,
∴y=x﹣1,
设P(a,a2+4a﹣1),则Q(a,a﹣1),
∴PQ=﹣a2﹣3a,
∴S△PAB=×3×(﹣a2﹣3a)=﹣(a﹣)2+,
∴当a=时,△PAB的面积有最大值;
(3)设点C(﹣2,y),
∵A(0,﹣1),B(﹣3,﹣4),
∴AB2=32+32=18,BC2=22+(y+1)2,AC2=12+(y+4)2,
①当AB=BC时,
∴22+(y+1)2=18,
解得,
∴;
②当AB=AC时,
∴12+(y+4)2=18,
解得,
∴;
③当BC=AC时,
∴22+(y+1)2=12+(y+4)2,
解得y=﹣2,
∴C(﹣2,﹣2);
综上所述:C点坐标为或或(﹣2,﹣2).
17.在平面直角坐标系中,过点A(3,4)的抛物线y=ax2+bx+4与x轴交于点B(﹣1,0),与y轴交于点C,过点A作AD⊥x轴于点D.
(1)求抛物线的解析式.
(2)如图1,点P是直线AB上方抛物线上的一个动点,连接PD交AB于点Q,连接AP,当S△AQD=2S△APQ时,求点P的坐标.
(3)如图2,点G是线段OC上一个动点,连结DG,求DG+CG的最小值.
【解答】解:(1)将点A(3,4),B(﹣1,0)代入y=ax2+bx+4,
得:,
解得,
∴y=﹣x2+3x+4;
(2)如图1,过点P作PE∥x轴,交AB于点E,
∵A(3,4),AD⊥x轴,
∴D(3,0),
∵B(﹣1,0),
∴BD=3﹣(﹣1)=4,
∵S△AQD=2S△APQ,△AQD与△APQ是等高的两个三角形,
∴=,
∵PE∥x轴,
∴△PQE∽△DQB,
∴==,
∴=,
∴PE=2,
∴可求得直线AB的解析式为y=x+1,
设E(x,x+1),则P(x﹣2,x+1),
将点P坐标代入y=﹣x2+3x+4得﹣(x﹣2)2+3(x﹣2)+4=x+1,
解得x1=3+,x2=3﹣,
当x=3+时,x﹣2=3+﹣2=1+,x+1=3++1=4+,
∴点P(1+,4+);
当x=3﹣时,x﹣2=3﹣﹣2=1﹣,x+1=3﹣+1=4﹣,
∴P(1﹣,4﹣),
∵点P是直线AB上方抛物线上的一个动点,
∴﹣1<x﹣2<3,
∴点P的坐标为(1+,4+)或(1﹣,4﹣);
(3)如图,以点C为顶点在y轴右侧作∠GCH=30°,过点G作GH⊥CH于点H,
在Rt△CHG中,HG=CG,
∴DG+CG=DG+GH,且当点D,G,H三点共线时,即DH⊥CH时,取得最小值DH,如下图,
此时∠DGO=∠CGH=60°,
∴∠ODG=30°,
∴OG=OD=,
∴CG=4﹣,DG=2OG=2,
∴HG=CG=2﹣,
∴DH=HG+DG=2+.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
二次函数综合问题“五大题型”
胡不归问题
11.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣4与x轴交于A,B两点(B在A的右侧),与y轴交于点C,已知OA=1,OB=4OA,连接BC.
(1)求抛物线的解析式;
(2)如图1,点P为BC下方抛物线上一动点,连接BP、CP,当S△BCP=S△BOC时,求点P的坐标;
(3)如图2,点N为线段OC上一点,求AN+CN的最小值.
相似问题
12.如图,已知抛物线y=﹣x2+bx+c经过点A(﹣3,0),C(0,3),交x轴于另一点B,其顶点为D.
(1)求抛物线的解析式;
(2)P为x轴上一点,若△CAP与△OCD相似,直接写出点P的坐标.
13.如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx经过点A(2,0)和点B(﹣1,m),顶点为点D.
(1)求直线AB的表达式;
(2)求tan∠ABD的值;
(3)设线段BD与x轴交于点P,如果点C在x轴上,且△ABC与△ABP相似,求点C的坐标.
平行四边形问题
14.如图,已知抛物线y=x2+bx+c的对称轴为直线x=4,与y轴相交于点B(0,﹣5).
(1)求抛物线的函数解析式;
(2)求直线AB的解析式并直接写出线段AB的中点M的坐标;
(3)设动点P,Q分别在抛物线和对称轴l上,当以A,P,Q,M为顶点的四边形是平行四边形时,直接写出Q点的坐标.
直角三角形问题
15.如图,直线y=x+b和抛物线y=ax2﹣x+2都经过A(0,n)和B(m,4)两点,抛物线y=ax2﹣x+2与x轴交于C、D两点(点C在点D右侧).
(1)求直线和抛物线的函数表达式;
(2)求四边形ABCD的面积S;
(3)在x轴上是否存在点P,使得△PAB是以AP为直角边的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.
等腰三角形问题
16.如图,在平面直角坐标系中,已知抛物线y=x2+bx+c与直线AB相交于A,B两点,其中A(﹣3,﹣4),B(0,﹣1).
(1)求该抛物线的函数表达式.
(2)点P为直线AB下方抛物线上的任意一点,连接PA,PB,求△PAB面积的最大值.
(3)在二次函数的对称轴上找一点C,使得△ABC是等腰三角形,求满足条件的点C的坐标.
练习题(作业)
17.在平面直角坐标系中,过点A(3,4)的抛物线y=ax2+bx+4与x轴交于点B(﹣1,0),与y轴交于点C,过点A作AD⊥x轴于点D.
(1)求抛物线的解析式.
(2)如图1,点P是直线AB上方抛物线上的一个动点,连接PD交AB于点Q,连接AP,当S△AQD=2S△APQ时,求点P的坐标.
(3)如图2,点G是线段OC上一个动点,连结DG,求DG+CG的最小值.
参考答案与试题解析
11.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣4与x轴交于A,B两点(B在A的右侧),与y轴交于点C,已知OA=1,OB=4OA,连接BC.
(1)求抛物线的解析式;
(2)如图1,点P为BC下方抛物线上一动点,连接BP、CP,当S△BCP=S△BOC时,求点P的坐标;
(3)如图2,点N为线段OC上一点,求AN+CN的最小值.
【解答】解:(1)∵OA=1,OB=4OA,
∴OB=4,
∴A(﹣1,0),B(4,0),
将A,B坐标代入抛物线解析式得,,
解得,
∴抛物线的解析式为:y=x2﹣3x﹣4;
(2)过点P作y轴的平行线,交BC于点Q,
设点P的横坐标为t,则P(t,t2﹣3t﹣4),
由(1)知抛物线的解析式为y=x2﹣3x﹣4,
令x=0,则y=﹣4,
∴C(0,﹣4),
∴OB=OC=4,
∴S△BOC=×4×4=8.
设直线BC的解析式为y=mx+n,
则,解得,
∴直线MN的解析式为y=x﹣4,
∴Q(t,t﹣4),
∴QP=t﹣4﹣(t2﹣3t﹣4)=﹣t2+4t,
∴S△BCP=S△BCP+S△BCP=PQ (xB﹣xQ)+PQ (xQ﹣xC)=PQ (xB﹣xC)= (﹣t2+4t)×(4﹣0)=﹣2t2+8t,
∵S△BCP=S△BOC,
∴﹣2t2+8t=8,
解得t=2;
此时y=22﹣3×2﹣4=﹣6,
∴P(2,﹣6);
(3)如图,过点N作NM⊥BC于点M,
∴∠CMN=90°,
由(2)知,OB=OC=4,
∴∠OBC=∠OCB=45°,
∴△CNM是等腰直角三角形,
∴NM=CN,
∴AN+CN=AN+NM,
则当A,N,M三点共线时,即AM⊥BC时,取到最小值,如图,过点A作AM′⊥BC于点M′,
则△AM′B是等腰直角三角形,
∴AM′=AB=.
∴AN+CN的最小值为:.
12.如图,已知抛物线y=﹣x2+bx+c经过点A(﹣3,0),C(0,3),交x轴于另一点B,其顶点为D.
(1)求抛物线的解析式;
(2)P为x轴上一点,若△CAP与△OCD相似,直接写出点P的坐标.
【解答】解:(1)把A(﹣3,0),C(0,3)代入抛物线解析式,,
解得,
∴抛物线的解析式为:y=﹣x2﹣2x+3;
(2)由(1)知,y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴点D(﹣1,4),
如图,过点D作DE⊥y轴于点E,
则DE=1,OE=4,
∵OC=3,
∴CE=1,
∴DE=CE,
∴∠DCE=45°,CD=,
∴∠OCD=135°,CD:OC=:3;
∵A(﹣3,0),C(0,3),
∴OA=OC=3,
∴∠OAC=∠OCA=45°,AC=3,
若△CAP与△OCD相似,点P只能在点A的左侧,
此时∠PAC=135°,且AP:AC=CD:OC或AP:AC=OC:CD,
∴AP:3=:3,或AP:3=3:,
解得AP=2或AP=9,
即P(﹣5,0)或P(﹣12,0).
13.如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx经过点A(2,0)和点B(﹣1,m),顶点为点D.
(1)求直线AB的表达式;
(2)求tan∠ABD的值;
(3)设线段BD与x轴交于点P,如果点C在x轴上,且△ABC与△ABP相似,求点C的坐标.
【解答】解:(1)将A(2,0)代入y=x2+bx,
∴4+2b=0,
∴b=﹣2,
∴y=x2﹣2x,
将B(﹣1,m)代入y=x2﹣2x,
∴m=3,
∴B(﹣1,3),
设直线AB的解析式为y=kx+b,
∴,
∴,
∴y=﹣x+2;
(2)∵y=x2﹣2x=(x﹣1)2﹣1,
∴D(1,﹣1),
∴AD=,AB=2,BC=3,
∵AB2=AD2+BC2,
∴△ABD是直角三角形,
∴tan∠ABD==;
(3)设直线BD的解析式为y=k1x+b1,
∴,
∴,
∴y=﹣2x+1,
令y=0,则x=,
∴P(,0),
设C(t,0),
如图1,当∠ABC=∠APB时,△ABP∽△APC,
∴∠ACB=∠ABP,
过B点作BQ⊥x轴交于点Q,
∴tan∠BCQ==,
∴CQ=9,
∴CO=10,
∴C(﹣10,0);
如图2,当∠PBC=∠BAP时,△ABP∽△BCP,
∴∠ABP=∠BCP,
过B点作BQ⊥x轴交于点Q,
∴tan∠BCP===,
∴CG=9,
∴OC=8,
∴C(8,0);
综上所述:C点的坐标为(﹣10,0)或(8,0).
14.如图,已知抛物线y=x2+bx+c的对称轴为直线x=4,与y轴相交于点B(0,﹣5).
(1)求抛物线的函数解析式;
(2)求直线AB的解析式并直接写出线段AB的中点M的坐标;
(3)设动点P,Q分别在抛物线和对称轴l上,当以A,P,Q,M为顶点的四边形是平行四边形时,直接写出Q点的坐标.
【解答】解:(1)根据题意可知,x=﹣=4,a=﹣,解得b=4;
将点B(0,﹣5)代入抛物线解析式可得c=﹣5,
∴抛物线的表达式为:y=﹣x2+4x﹣5;
(2)∵y=﹣x2+4x﹣5=﹣(x﹣4)2+3,
∴A(4,3),B(0,﹣5),
∴点M(2,﹣1),
设直线AB的表达式为:y=kx﹣5,
将点A坐标代入上式得:3=4k﹣5,解得:k=2,
∴直线AB的表达式为:y=2x﹣5;
(3)设点Q(4,s)、点P(m,﹣m2+4m﹣5),
①当AM是平行四边形的一条边时,
当点Q在A的下方时,
点A向左平移2个单位、向下平移4个单位得到M,
同样点P(m,﹣m2+4m﹣5)向左平移2个单位、向下平移4个单位得到Q(4,s),
即:m﹣2=4,﹣m2+4m﹣5﹣4=s,
解得:m=6,s=﹣3,
∴点Q的坐标为(4,﹣3),
故当点Q在点A上方时,AQ=MP=2,
同理可得点Q的坐标为(4,5),
②当AM是平行四边形的对角线时,
由中点定理得:4+2=m+4,3﹣1=﹣m2+4m﹣5+s,
解得:m=2,s=1,
∴Q的坐标分别为(4,1);
综上,Q的坐标分别为Q(4,﹣3)或(4,1)或(4,5).
15.如图,直线y=x+b和抛物线y=ax2﹣x+2都经过A(0,n)和B(m,4)两点,抛物线y=ax2﹣x+2与x轴交于C、D两点(点C在点D右侧).
(1)求直线和抛物线的函数表达式;
(2)求四边形ABCD的面积S;
(3)在x轴上是否存在点P,使得△PAB是以AP为直角边的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.
【解答】解:(1)把(0,n)代入y=ax2﹣x+2中得,
n=2,即A(0,2),
把(0,2)代入y=x+b中得,
b=2,
∴y=x+2,
把B(m,4)代入y=x+2中得,
+2=4,
∴m=6,即B(6,4),
把B(6,4)代入y=ax2﹣x+2中得,36a﹣10+2=4,
∴a=,即y=x2﹣x+2,
∴直线表达式是y=x+2,
抛物线解析式为:y=x2﹣x+2;
(2)解方程x2﹣x+2=0,得
x1=2,x2=3,
∵点C在点D右侧,
∴C(3,0),D(2,0),
过B作BE⊥y轴于E,作BF⊥x轴于F,
∴E(6,0),
∵A(0,2),B(6,4),C(3,0),D(2,0),
∴AO=2,DO=2,CE=3,BE=4,OE=6,
∴S四边形ABCD=S梯形ABCD﹣S△AOD﹣S△BCE
=(AO+BE) OE﹣AO OD﹣BE CE
=×(2+4)×6﹣×2×2﹣×3×4
=18﹣2﹣6
=10,即四边形ABCD的面积为10;
(3)设P(t,0),A(0,2),B(6,4),
∴PA2=t2+4,BP2=(t﹣6)2+16,
AB2=36+4=40,
①当∠PAB=90°时,
∴t2+4+40=(t﹣6)2+16,
∴t=,即P(,0);
②当∠APB=90°时,
∴t2+4+(t﹣6)2+16+40,
∴x=2或4,
∴P(2,0)或P(4,0),
综上所述△PAB以AP为直角边时,P(,0)或P(2,0)或P(4,0).
16.如图,在平面直角坐标系中,已知抛物线y=x2+bx+c与直线AB相交于A,B两点,其中A(﹣3,﹣4),B(0,﹣1).
(1)求该抛物线的函数表达式.
(2)点P为直线AB下方抛物线上的任意一点,连接PA,PB,求△PAB面积的最大值.
(3)在二次函数的对称轴上找一点C,使得△ABC是等腰三角形,求满足条件的点C的坐标.
【解答】解:(1)将A(﹣3,﹣4),B(0,﹣1)代入y=x2+bx+c,
得,
解得,
∴y=x2+4x﹣1;
(2)设直线AB的解析式为y=kx+b,
则,
解得,
∴y=x﹣1,
设P(a,a2+4a﹣1),则Q(a,a﹣1),
∴PQ=﹣a2﹣3a,
∴S△PAB=×3×(﹣a2﹣3a)=﹣(a﹣)2+,
∴当a=时,△PAB的面积有最大值;
(3)设点C(﹣2,y),
∵A(0,﹣1),B(﹣3,﹣4),
∴AB2=32+32=18,BC2=22+(y+1)2,AC2=12+(y+4)2,
①当AB=BC时,
∴22+(y+1)2=18,
解得,
∴;
②当AB=AC时,
∴12+(y+4)2=18,
解得,
∴;
③当BC=AC时,
∴22+(y+1)2=12+(y+4)2,
解得y=﹣2,
∴C(﹣2,﹣2);
综上所述:C点坐标为或或(﹣2,﹣2).
17.在平面直角坐标系中,过点A(3,4)的抛物线y=ax2+bx+4与x轴交于点B(﹣1,0),与y轴交于点C,过点A作AD⊥x轴于点D.
(1)求抛物线的解析式.
(2)如图1,点P是直线AB上方抛物线上的一个动点,连接PD交AB于点Q,连接AP,当S△AQD=2S△APQ时,求点P的坐标.
(3)如图2,点G是线段OC上一个动点,连结DG,求DG+CG的最小值.
【解答】解:(1)将点A(3,4),B(﹣1,0)代入y=ax2+bx+4,
得:,
解得,
∴y=﹣x2+3x+4;
(2)如图1,过点P作PE∥x轴,交AB于点E,
∵A(3,4),AD⊥x轴,
∴D(3,0),
∵B(﹣1,0),
∴BD=3﹣(﹣1)=4,
∵S△AQD=2S△APQ,△AQD与△APQ是等高的两个三角形,
∴=,
∵PE∥x轴,
∴△PQE∽△DQB,
∴==,
∴=,
∴PE=2,
∴可求得直线AB的解析式为y=x+1,
设E(x,x+1),则P(x﹣2,x+1),
将点P坐标代入y=﹣x2+3x+4得﹣(x﹣2)2+3(x﹣2)+4=x+1,
解得x1=3+,x2=3﹣,
当x=3+时,x﹣2=3+﹣2=1+,x+1=3++1=4+,
∴点P(1+,4+);
当x=3﹣时,x﹣2=3﹣﹣2=1﹣,x+1=3﹣+1=4﹣,
∴P(1﹣,4﹣),
∵点P是直线AB上方抛物线上的一个动点,
∴﹣1<x﹣2<3,
∴点P的坐标为(1+,4+)或(1﹣,4﹣);
(3)如图,以点C为顶点在y轴右侧作∠GCH=30°,过点G作GH⊥CH于点H,
在Rt△CHG中,HG=CG,
∴DG+CG=DG+GH,且当点D,G,H三点共线时,即DH⊥CH时,取得最小值DH,如下图,
此时∠DGO=∠CGH=60°,
∴∠ODG=30°,
∴OG=OD=,
∴CG=4﹣,DG=2OG=2,
∴HG=CG=2﹣,
∴DH=HG+DG=2+.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
