2021-2022学年北师大版九年级数学下册第2章二次函数寒假自主达标测试(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册第2章二次函数寒假自主达标测试(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 144.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 15:53:39 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学下册《第2章二次函数》寒假自主达标测试(附答案)
一.选择题(共10小题,满分50分)
1.函数y=x2﹣6x+9向左平移m个单位后其图象恰好经过坐标原点,则m的值为( )
A.﹣3 B.﹣1 C.3 D.﹣1或3
2.如图,抛物线y1=ax2+bx+c与直线y2=kx+m的交点为A(1,﹣3),B(6,1).当y1>y2时,x的取值范围是( )
A.1<x<6 B.﹣3<x<1 C.x<﹣3或x>1 D.x<1或x>6
3.飞机着陆后滑行的距离s(单位:m)与滑行的时间t(单位:s)的函数解析式是s=60t﹣1.5t2,那么飞机着陆后滑行多长时间才能停下来( )
A.10s B.20s C.30s D.40s
4.如图,在平面直角坐标系xOy中,已知点A的坐标为(5,0),点B的坐标为B(m,m).若m>0,△OAB的面积为,过A、B、O三点的抛物线上有异于A、B、O的一点M,点M的坐标为M(a,3),则a的值为( )
A.2 B.3 C.4 D.5
5.在同一平面直角坐标系中,若抛物线y=x2+(2m﹣1)x+2m﹣4与y=﹣x2﹣(3m+n)x+n关于x轴对称,则符合条件的m,n的值为( )
A.m=,n= B.m=5,n=﹣6
C.m=﹣1,n=6 D.m=1,n=﹣2
6.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:
①abc>0;②b2<4ac;③9a+3b+c<0;④2c<3b.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
7.正方形ABCD中,AB=4,P为对角线BD上一动点,F为射线AD上一点,若AP=PF,则△APF的面积最大值为( )
A.8 B.6 C.4 D.2
8.如图,抛物线y=ax2+bx+c经过(﹣1,0)和(0,﹣1)两点,则抛物线y=cx2+bx+a的图象大致为( )
A. B. C. D.
9.已知二次函数y=2x2﹣8x+6的图象交x轴于A,B两点.若其图象上有且只有P1,P2,P3三点满足===m,则m的值是( )
A.1 B. C.2 D.4
10.若点A(m﹣1,y1),B(m,y2)都在二次函数y=ax2+4ax+3(a<0)的图象上,且y1>y2,则m的取值范围是( )
A.m≤﹣1 B.m≥﹣1 C.m<﹣ D.m>﹣
二.填空题(共6小题,满分,30分)
11.如图,抛物线y=﹣x2﹣x+与x轴相交于点A,B,与y轴相交于点C,则△ABC的面积为 .
12.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,与x轴的一个交点是(3,0),则方程ax2+bx+c=0(a≠0)的两根是 .
13.如图,单孔拱桥的形状近似抛物线形,建立如图所示的平面直角坐标系,在正常水位时,水面宽度OA为12m,拱桥的最高点B到水面OA的距离为6m.则抛物线的解析式为 .
14.为了在体育中考中取得更好的成绩,小明积极训练,体育老师对小明投掷铅球的录像进行技术分析,如图,发现铅球在行进过程中高度y(m)与水平距离x(m)之间的关系为y=﹣(x﹣2)2+2,由此可知小明此次投掷的成绩是 m.
15.如图,P是抛物线y=x2﹣2x﹣3在第四象限的一点,过点P分别向x轴和y轴作垂线,垂足分别为A、B,则四边形OAPB周长的最大值为 .
16.已知抛物线y=ax2+bx+c(a,b,c是常数)中,4a﹣b=0,a﹣b+c>0,抛物线与x轴的两交点之间的距离小于2,且经过点(0,3).下列四个结论:
①对称轴为直线x=﹣2;
②若点(m﹣2,y1)和(n﹣2,y2)在抛物线上,且m>n,则y1>y2;
③一元二次方程ax2+bx+c=0的一个根在﹣2和﹣3之间;
④0<a<1;
其中结论正确结论是 (填写序号).
三.解答题(共4小题,满分40分)
17.已知关于x的一元二次方程x2+x﹣m=0.
(1)若方程有两个不相等的实数根,求m的取值范围;
(2)二次函数y=x2+x﹣m的部分图象如图所示,求一元二次方程x2+x﹣m=0的解.
18.已知抛物线:y=x2﹣2x﹣3,抛物线图象与x轴交于A,B两点(点B在点A的右边).
(1)求A,B两点间的距离及抛物线的顶点坐标.
(2)若将该抛物线沿垂直方向向上平移1个单位,再沿水平方向向右平移若干个单位后,新的抛物线刚好经过点B.求平移后新的抛物线表达式.
19.近期多次出现进口冷冻牛肉外包装新冠病毒核酸呈阳性,国内的新鲜牛肉价格出现了大幅度涨价.某牛肉摊位购进一批国产新鲜牛肉,进价为每千克40元,物价部门规定其销售价不低于成本价且不高于成本价的2倍.经试销发现,日销售量y(千克)与销售单价x(元/千克)符合如图所示的一次函数关系:
(1)求y与x的函数关系式,并写出自变量x的取值范围;
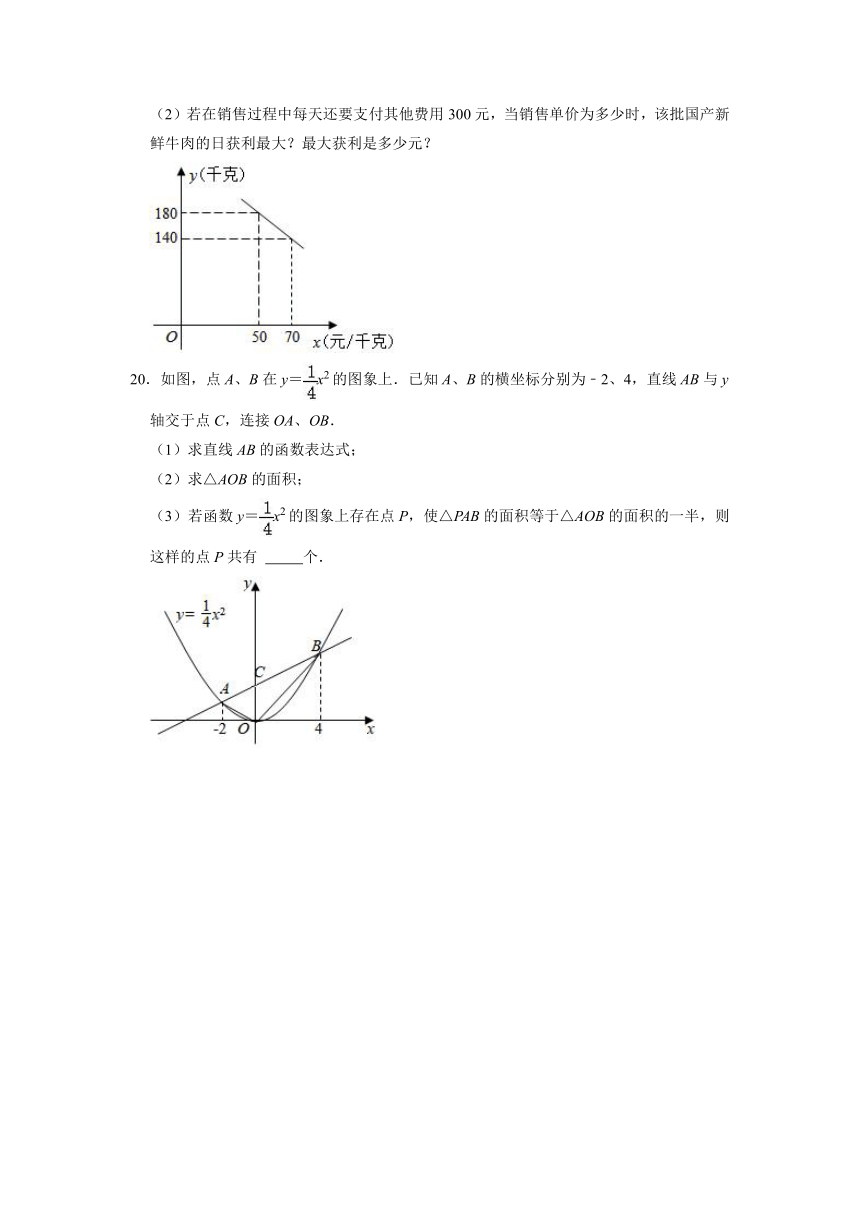
(2)若在销售过程中每天还要支付其他费用300元,当销售单价为多少时,该批国产新鲜牛肉的日获利最大?最大获利是多少元?
20.如图,点A、B在y=x2的图象上.已知A、B的横坐标分别为﹣2、4,直线AB与y轴交于点C,连接OA、OB.
(1)求直线AB的函数表达式;
(2)求△AOB的面积;
(3)若函数y=x2的图象上存在点P,使△PAB的面积等于△AOB的面积的一半,则这样的点P共有 个.
参考答案
一.选择题(共10小题,满分50分)
1.解:∵y=x2﹣6x+9=(x﹣3)2,
∴向左平移m个单位后的函数解析式为y=(x﹣3+m)2,
∵函数图象经过坐标原点,
∴(0﹣3+m)2=0,
解得m=3.
故选:C.
2.解:∵二次函数y1=ax2+bx+c与一次函数y2=kx+m的交点A、B的坐标分别为(1,﹣3)、(6,1),
∴当y1>y2时,x的取值范围是x<1或x>6,
故选:D.
3.解:∵a=﹣1.5<0,
∴函数有最大值,
当t=﹣=﹣=20(秒),
即飞机着陆后滑行20秒能停下来,
故选:B.
4.解:∵点A的坐标为(5,0),
∴OA=5,
∵点B的坐标为B(m,m),且m>0,△OAB的面积为,
∴=.
∴m=3,
∴B(3,3),
∵抛物线经过原点和点A(5,0),
∴抛物线对称轴为直线x=,
∵点M(a,3),
∴=,
∴a=2,
故选:A.
5.解:∵抛物线y=x2+(2m﹣1)x+2m﹣4与y=﹣x2﹣(3m+n)x+n关于x轴对称,
∴﹣y=x2+(3m+n)x﹣n,
∴x2+(3m+2n)x﹣n=x2+(2m﹣1)x+2m﹣4,
∴,
解得,
故选:B.
6.解:①函数对称轴在y轴右侧,则ab<0,c>0,故①错误,不符合题意;
②抛物线与x轴有两个交点,则b2﹣4ac>0,所以b2>4ac,故②错误,不符合题意;
③x=3时,y=9a+3b+c<0,故正确,符合题意;
④函数的对称轴为:x=1,故b=﹣2a,而由②知:b>a+c,故2c<3b正确,符合题意;
故选:B.
7.解:作PM⊥AD与M,
∵BD是正方形ABCD的对角线,
∴∠ADB=45°,
∴△PDM是等腰直角三角形,
∴PM=DM,
设PM=DM=x,则AM=4﹣x,
∵AP=PF,
∴AM=FM=4﹣x,
∴AF=2(4﹣x),
∵S△APF=AF PM,
∴S△APF=×2(4﹣x) x=﹣x2+4x=﹣(x﹣2)2+4,
∴当x=2时,S△APF有最大值4,
故选:C.
8.解:∵抛物线y=ax2+bx+c经过(﹣1,0)和(0,﹣1)两点,
∴开口向上,对称轴在y轴的右侧,
∴a﹣b+c=0,a>0,b<0,c=﹣1,
∴抛物线y=cx2+bx+a的开口向下,对称轴直线x=﹣<0,交y轴正半轴,
当x=﹣1时,y=c﹣b+a=0,
∴抛物线y=cx2+bx+a经过点(﹣1,0),
故选:B.
9.解:∵二次函数y=2x2﹣8x+6的图象上有且只有P1,P2,P3三点满足===m,
∴三点中必有一点在二次函数y=2x2﹣8x+6的顶点上,
∵y=2x2﹣8x+6=2(x﹣2)2﹣2=2(x﹣1)(x﹣3),
∴二次函数y=2x2﹣8x+6的图象的顶点坐标为(2,﹣2),
令y=0,则2(x﹣1)(x﹣3)=0,
解得x=1或x=3,
∴与x轴的交点为(1,0),(3,0),
∴AB=3﹣1=2,
∴m==2.
故选:C.
10.解:抛物线的对称轴为直线x=﹣=﹣2,
∵m﹣1<m,y1>y2,
∴当点A(m﹣1,y1)和B(m,y2)在直线x=﹣2的右侧,则m﹣1≥﹣2,解得m≥﹣1;
当点A(m﹣1,y1)和B(m,y2)在直线x=﹣2的两侧,则﹣2﹣(m﹣1)<m﹣(﹣2),解得m>﹣;
综上所述,m的范围为m>﹣.
故选:D.
二.填空题(共6小题,满分30分)
11.解:∵抛物线y=﹣x2﹣x+,
∴当y=0时,x1=﹣3,x2=1,当x=0时,y=,
∴点A的坐标为(﹣3,0),点B的坐标为(1,0),点C的坐标为(0,),
∴AB=1﹣(﹣3)=1+3=4,OC=,
∴△ABC的面积为:=3,
故答案为:3.
12.解:∵抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,与x轴的一个交点是(3,0),
∴抛物线与x轴的另一个交点为(﹣1,0),
∴当y=0时,0=ax2+bx+c的两个根为x=3或x=﹣1.
故答案为:x=3或x=﹣1.
13.解:∵水面宽度OA为12m,拱桥的最高点B到水面OA的距离为6m.
∴B(6,6),A(12,0),
设抛物线的解析式为y=a(x﹣6)2+6,
∴y=a(12﹣6)2+6,
∴0=a 62+6,
解得a=﹣,
∴抛物线的解析式为y=﹣(x﹣6)2+6;
故答案为:y=﹣(x﹣6)2+6.
14.解:由题意,得
当y=0时,﹣(x﹣2)2+2=0,
化简,得:(x﹣2)2=25,
解得:x1=7,x2=﹣3(舍去),
故答案为:7.
15.解:设P(x,x2﹣2x﹣3),
∵过点P分别向x轴和y轴作垂线,垂足分别为A、B,
∴四边形OAPB为矩形,
∴四边形OAPB周长=2PA+2OA
=﹣2(x2﹣2x﹣3)+2x
=﹣2x2+6x+6
=﹣2(x2﹣3x)+6,
=﹣2+.
∴当x=时,四边形OAPB周长有最大值,最大值为.
故答案为.
16.解:①∵4a﹣b=0,∴b=4a,对称轴是直线:x=﹣=﹣=﹣2,所以①正确,符合题意;
②∵m>n,∴m﹣2>n﹣2,只能确定出m﹣2和n﹣2的大小关系,即横坐标的大小关系,而要进一步确定纵坐标y1,y2,的大小关系,是必须知道横坐标与对称轴的关系,而题目中没办法给出在对称轴的同侧还是异侧,若都在对称轴的左侧故②错误,不合题意;
③由①知,对称轴是直线x=﹣2,抛物线与x轴的两交点就是在点(﹣2,0)左右两侧,且关于直线x=﹣2对称,又知道抛物线与x轴的两交点之间的距离小于2,所以一个根在﹣2和﹣3之间,另一个根在﹣2和﹣1之间,所以③正确,符合题意;
④,
解得<a<1,故④错误,不合题意.
故答案是:①③.
三.解答题(共4小题,满分40分)
17.解:(1)∵一元二次方程x2+x﹣m=0有两个不相等的实数根,
∴Δ>0,即1+4m>0,
∴m>﹣;
(2)二次函数y=x2+x﹣m图象的对称轴为直线x=﹣,
∴抛物线与x轴两个交点关于直线x=﹣对称,
由图可知抛物线与x轴一个交点为(1,0),
∴另一个交点为(﹣2,0),
∴一元二次方程x2+x﹣m=0的解为x1=1,x2=﹣2.
18.解:(1)由x2﹣2x﹣3=0,得:x=﹣1或=3,
∴AB=|﹣1﹣3|=4,
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴顶点坐标为 (1,﹣4);
(2)设新抛物线表达式:y=(x﹣m)2﹣3,把(3,0)代入得:m=3±,
∴新抛物线表达式:y=(x﹣3+)2﹣3或y=(x﹣3﹣)2﹣3.
19.解:(1)设一次函数关系式为y=kx+b(k≠0),
由图象可得,当x=50时,y=180;x=70时,y=140,
∴,
解得:,销售单价不低于成本价且不高于成本价的2倍,40≤x≤80,
∴y与x之间的关系式为:y=﹣2x+280(40≤x≤80);
(2)设该公司日获利为W元,由题意得W=(x﹣40)(﹣2x+280)﹣300=﹣2(x﹣90)2+4700,
∵a=﹣2<0,
∴抛物线开口向下,
∵对称轴直线x=90,
∴当x<90时,W随x的增大而增大,
∵40≤x≤80,
∴x=80时,W有最大值,
Wmax=﹣2×(80﹣90)2+4700=4500,
故当销售单价为每千克80元时,日获利最大,最大获利为4500元.
20.解:(1)∵点A、B在y=x2的图象上,A、B的横坐标分别为﹣2、4,
∴A(﹣2,1),B(4,4),
设直线AB的解析式为y=kx+b,
∴,解得,
∴直线AB的解析式为y=+2;
(2)在y=+2中,令x=0,则y=2,
∴C的坐标为(0,2),
∴OC=2,
∴S△AOB=S△AOC+S△BOC=+=6.
(3)过OC的中点,作AB的平行线交抛物线两个交点P1、P2,此时△P1AB的面积和△P2AB的面积等于△AOB的面积的一半,
作直线P1P2关于直线AB的对称直线,交抛物线两个交点P3、P4,此时△P3AB的面积和△P4AB的面积等于△AOB的面积的一半,
所以这样的点P共有4个,
故答案为4.
一.选择题(共10小题,满分50分)
1.函数y=x2﹣6x+9向左平移m个单位后其图象恰好经过坐标原点,则m的值为( )
A.﹣3 B.﹣1 C.3 D.﹣1或3
2.如图,抛物线y1=ax2+bx+c与直线y2=kx+m的交点为A(1,﹣3),B(6,1).当y1>y2时,x的取值范围是( )
A.1<x<6 B.﹣3<x<1 C.x<﹣3或x>1 D.x<1或x>6
3.飞机着陆后滑行的距离s(单位:m)与滑行的时间t(单位:s)的函数解析式是s=60t﹣1.5t2,那么飞机着陆后滑行多长时间才能停下来( )
A.10s B.20s C.30s D.40s
4.如图,在平面直角坐标系xOy中,已知点A的坐标为(5,0),点B的坐标为B(m,m).若m>0,△OAB的面积为,过A、B、O三点的抛物线上有异于A、B、O的一点M,点M的坐标为M(a,3),则a的值为( )
A.2 B.3 C.4 D.5
5.在同一平面直角坐标系中,若抛物线y=x2+(2m﹣1)x+2m﹣4与y=﹣x2﹣(3m+n)x+n关于x轴对称,则符合条件的m,n的值为( )
A.m=,n= B.m=5,n=﹣6
C.m=﹣1,n=6 D.m=1,n=﹣2
6.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:
①abc>0;②b2<4ac;③9a+3b+c<0;④2c<3b.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
7.正方形ABCD中,AB=4,P为对角线BD上一动点,F为射线AD上一点,若AP=PF,则△APF的面积最大值为( )
A.8 B.6 C.4 D.2
8.如图,抛物线y=ax2+bx+c经过(﹣1,0)和(0,﹣1)两点,则抛物线y=cx2+bx+a的图象大致为( )
A. B. C. D.
9.已知二次函数y=2x2﹣8x+6的图象交x轴于A,B两点.若其图象上有且只有P1,P2,P3三点满足===m,则m的值是( )
A.1 B. C.2 D.4
10.若点A(m﹣1,y1),B(m,y2)都在二次函数y=ax2+4ax+3(a<0)的图象上,且y1>y2,则m的取值范围是( )
A.m≤﹣1 B.m≥﹣1 C.m<﹣ D.m>﹣
二.填空题(共6小题,满分,30分)
11.如图,抛物线y=﹣x2﹣x+与x轴相交于点A,B,与y轴相交于点C,则△ABC的面积为 .
12.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,与x轴的一个交点是(3,0),则方程ax2+bx+c=0(a≠0)的两根是 .
13.如图,单孔拱桥的形状近似抛物线形,建立如图所示的平面直角坐标系,在正常水位时,水面宽度OA为12m,拱桥的最高点B到水面OA的距离为6m.则抛物线的解析式为 .
14.为了在体育中考中取得更好的成绩,小明积极训练,体育老师对小明投掷铅球的录像进行技术分析,如图,发现铅球在行进过程中高度y(m)与水平距离x(m)之间的关系为y=﹣(x﹣2)2+2,由此可知小明此次投掷的成绩是 m.
15.如图,P是抛物线y=x2﹣2x﹣3在第四象限的一点,过点P分别向x轴和y轴作垂线,垂足分别为A、B,则四边形OAPB周长的最大值为 .
16.已知抛物线y=ax2+bx+c(a,b,c是常数)中,4a﹣b=0,a﹣b+c>0,抛物线与x轴的两交点之间的距离小于2,且经过点(0,3).下列四个结论:
①对称轴为直线x=﹣2;
②若点(m﹣2,y1)和(n﹣2,y2)在抛物线上,且m>n,则y1>y2;
③一元二次方程ax2+bx+c=0的一个根在﹣2和﹣3之间;
④0<a<1;
其中结论正确结论是 (填写序号).
三.解答题(共4小题,满分40分)
17.已知关于x的一元二次方程x2+x﹣m=0.
(1)若方程有两个不相等的实数根,求m的取值范围;
(2)二次函数y=x2+x﹣m的部分图象如图所示,求一元二次方程x2+x﹣m=0的解.
18.已知抛物线:y=x2﹣2x﹣3,抛物线图象与x轴交于A,B两点(点B在点A的右边).
(1)求A,B两点间的距离及抛物线的顶点坐标.
(2)若将该抛物线沿垂直方向向上平移1个单位,再沿水平方向向右平移若干个单位后,新的抛物线刚好经过点B.求平移后新的抛物线表达式.
19.近期多次出现进口冷冻牛肉外包装新冠病毒核酸呈阳性,国内的新鲜牛肉价格出现了大幅度涨价.某牛肉摊位购进一批国产新鲜牛肉,进价为每千克40元,物价部门规定其销售价不低于成本价且不高于成本价的2倍.经试销发现,日销售量y(千克)与销售单价x(元/千克)符合如图所示的一次函数关系:
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)若在销售过程中每天还要支付其他费用300元,当销售单价为多少时,该批国产新鲜牛肉的日获利最大?最大获利是多少元?
20.如图,点A、B在y=x2的图象上.已知A、B的横坐标分别为﹣2、4,直线AB与y轴交于点C,连接OA、OB.
(1)求直线AB的函数表达式;
(2)求△AOB的面积;
(3)若函数y=x2的图象上存在点P,使△PAB的面积等于△AOB的面积的一半,则这样的点P共有 个.
参考答案
一.选择题(共10小题,满分50分)
1.解:∵y=x2﹣6x+9=(x﹣3)2,
∴向左平移m个单位后的函数解析式为y=(x﹣3+m)2,
∵函数图象经过坐标原点,
∴(0﹣3+m)2=0,
解得m=3.
故选:C.
2.解:∵二次函数y1=ax2+bx+c与一次函数y2=kx+m的交点A、B的坐标分别为(1,﹣3)、(6,1),
∴当y1>y2时,x的取值范围是x<1或x>6,
故选:D.
3.解:∵a=﹣1.5<0,
∴函数有最大值,
当t=﹣=﹣=20(秒),
即飞机着陆后滑行20秒能停下来,
故选:B.
4.解:∵点A的坐标为(5,0),
∴OA=5,
∵点B的坐标为B(m,m),且m>0,△OAB的面积为,
∴=.
∴m=3,
∴B(3,3),
∵抛物线经过原点和点A(5,0),
∴抛物线对称轴为直线x=,
∵点M(a,3),
∴=,
∴a=2,
故选:A.
5.解:∵抛物线y=x2+(2m﹣1)x+2m﹣4与y=﹣x2﹣(3m+n)x+n关于x轴对称,
∴﹣y=x2+(3m+n)x﹣n,
∴x2+(3m+2n)x﹣n=x2+(2m﹣1)x+2m﹣4,
∴,
解得,
故选:B.
6.解:①函数对称轴在y轴右侧,则ab<0,c>0,故①错误,不符合题意;
②抛物线与x轴有两个交点,则b2﹣4ac>0,所以b2>4ac,故②错误,不符合题意;
③x=3时,y=9a+3b+c<0,故正确,符合题意;
④函数的对称轴为:x=1,故b=﹣2a,而由②知:b>a+c,故2c<3b正确,符合题意;
故选:B.
7.解:作PM⊥AD与M,
∵BD是正方形ABCD的对角线,
∴∠ADB=45°,
∴△PDM是等腰直角三角形,
∴PM=DM,
设PM=DM=x,则AM=4﹣x,
∵AP=PF,
∴AM=FM=4﹣x,
∴AF=2(4﹣x),
∵S△APF=AF PM,
∴S△APF=×2(4﹣x) x=﹣x2+4x=﹣(x﹣2)2+4,
∴当x=2时,S△APF有最大值4,
故选:C.
8.解:∵抛物线y=ax2+bx+c经过(﹣1,0)和(0,﹣1)两点,
∴开口向上,对称轴在y轴的右侧,
∴a﹣b+c=0,a>0,b<0,c=﹣1,
∴抛物线y=cx2+bx+a的开口向下,对称轴直线x=﹣<0,交y轴正半轴,
当x=﹣1时,y=c﹣b+a=0,
∴抛物线y=cx2+bx+a经过点(﹣1,0),
故选:B.
9.解:∵二次函数y=2x2﹣8x+6的图象上有且只有P1,P2,P3三点满足===m,
∴三点中必有一点在二次函数y=2x2﹣8x+6的顶点上,
∵y=2x2﹣8x+6=2(x﹣2)2﹣2=2(x﹣1)(x﹣3),
∴二次函数y=2x2﹣8x+6的图象的顶点坐标为(2,﹣2),
令y=0,则2(x﹣1)(x﹣3)=0,
解得x=1或x=3,
∴与x轴的交点为(1,0),(3,0),
∴AB=3﹣1=2,
∴m==2.
故选:C.
10.解:抛物线的对称轴为直线x=﹣=﹣2,
∵m﹣1<m,y1>y2,
∴当点A(m﹣1,y1)和B(m,y2)在直线x=﹣2的右侧,则m﹣1≥﹣2,解得m≥﹣1;
当点A(m﹣1,y1)和B(m,y2)在直线x=﹣2的两侧,则﹣2﹣(m﹣1)<m﹣(﹣2),解得m>﹣;
综上所述,m的范围为m>﹣.
故选:D.
二.填空题(共6小题,满分30分)
11.解:∵抛物线y=﹣x2﹣x+,
∴当y=0时,x1=﹣3,x2=1,当x=0时,y=,
∴点A的坐标为(﹣3,0),点B的坐标为(1,0),点C的坐标为(0,),
∴AB=1﹣(﹣3)=1+3=4,OC=,
∴△ABC的面积为:=3,
故答案为:3.
12.解:∵抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,与x轴的一个交点是(3,0),
∴抛物线与x轴的另一个交点为(﹣1,0),
∴当y=0时,0=ax2+bx+c的两个根为x=3或x=﹣1.
故答案为:x=3或x=﹣1.
13.解:∵水面宽度OA为12m,拱桥的最高点B到水面OA的距离为6m.
∴B(6,6),A(12,0),
设抛物线的解析式为y=a(x﹣6)2+6,
∴y=a(12﹣6)2+6,
∴0=a 62+6,
解得a=﹣,
∴抛物线的解析式为y=﹣(x﹣6)2+6;
故答案为:y=﹣(x﹣6)2+6.
14.解:由题意,得
当y=0时,﹣(x﹣2)2+2=0,
化简,得:(x﹣2)2=25,
解得:x1=7,x2=﹣3(舍去),
故答案为:7.
15.解:设P(x,x2﹣2x﹣3),
∵过点P分别向x轴和y轴作垂线,垂足分别为A、B,
∴四边形OAPB为矩形,
∴四边形OAPB周长=2PA+2OA
=﹣2(x2﹣2x﹣3)+2x
=﹣2x2+6x+6
=﹣2(x2﹣3x)+6,
=﹣2+.
∴当x=时,四边形OAPB周长有最大值,最大值为.
故答案为.
16.解:①∵4a﹣b=0,∴b=4a,对称轴是直线:x=﹣=﹣=﹣2,所以①正确,符合题意;
②∵m>n,∴m﹣2>n﹣2,只能确定出m﹣2和n﹣2的大小关系,即横坐标的大小关系,而要进一步确定纵坐标y1,y2,的大小关系,是必须知道横坐标与对称轴的关系,而题目中没办法给出在对称轴的同侧还是异侧,若都在对称轴的左侧故②错误,不合题意;
③由①知,对称轴是直线x=﹣2,抛物线与x轴的两交点就是在点(﹣2,0)左右两侧,且关于直线x=﹣2对称,又知道抛物线与x轴的两交点之间的距离小于2,所以一个根在﹣2和﹣3之间,另一个根在﹣2和﹣1之间,所以③正确,符合题意;
④,
解得<a<1,故④错误,不合题意.
故答案是:①③.
三.解答题(共4小题,满分40分)
17.解:(1)∵一元二次方程x2+x﹣m=0有两个不相等的实数根,
∴Δ>0,即1+4m>0,
∴m>﹣;
(2)二次函数y=x2+x﹣m图象的对称轴为直线x=﹣,
∴抛物线与x轴两个交点关于直线x=﹣对称,
由图可知抛物线与x轴一个交点为(1,0),
∴另一个交点为(﹣2,0),
∴一元二次方程x2+x﹣m=0的解为x1=1,x2=﹣2.
18.解:(1)由x2﹣2x﹣3=0,得:x=﹣1或=3,
∴AB=|﹣1﹣3|=4,
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴顶点坐标为 (1,﹣4);
(2)设新抛物线表达式:y=(x﹣m)2﹣3,把(3,0)代入得:m=3±,
∴新抛物线表达式:y=(x﹣3+)2﹣3或y=(x﹣3﹣)2﹣3.
19.解:(1)设一次函数关系式为y=kx+b(k≠0),
由图象可得,当x=50时,y=180;x=70时,y=140,
∴,
解得:,销售单价不低于成本价且不高于成本价的2倍,40≤x≤80,
∴y与x之间的关系式为:y=﹣2x+280(40≤x≤80);
(2)设该公司日获利为W元,由题意得W=(x﹣40)(﹣2x+280)﹣300=﹣2(x﹣90)2+4700,
∵a=﹣2<0,
∴抛物线开口向下,
∵对称轴直线x=90,
∴当x<90时,W随x的增大而增大,
∵40≤x≤80,
∴x=80时,W有最大值,
Wmax=﹣2×(80﹣90)2+4700=4500,
故当销售单价为每千克80元时,日获利最大,最大获利为4500元.
20.解:(1)∵点A、B在y=x2的图象上,A、B的横坐标分别为﹣2、4,
∴A(﹣2,1),B(4,4),
设直线AB的解析式为y=kx+b,
∴,解得,
∴直线AB的解析式为y=+2;
(2)在y=+2中,令x=0,则y=2,
∴C的坐标为(0,2),
∴OC=2,
∴S△AOB=S△AOC+S△BOC=+=6.
(3)过OC的中点,作AB的平行线交抛物线两个交点P1、P2,此时△P1AB的面积和△P2AB的面积等于△AOB的面积的一半,
作直线P1P2关于直线AB的对称直线,交抛物线两个交点P3、P4,此时△P3AB的面积和△P4AB的面积等于△AOB的面积的一半,
所以这样的点P共有4个,
故答案为4.
