高中数学人教新课标A版 空间几何体的外接球 课件(共29张PPT)
文档属性
| 名称 | 高中数学人教新课标A版 空间几何体的外接球 课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 09:13:41 | ||
图片预览


文档简介
(共29张PPT)
微专题:
空间几何体的外接球
厦门六中 郭祯
2015
2017
2018
2019
2020
感悟高考
延迟符
近几年新课标全国卷空间几何体外接球试题在题型、考查载体、考查能力、解题方法等方面呈现怎样的特征
01
考查以选择、填空题形式;难度中等;
02
载体以柱体、锥体为主,对空间想象能力要求较高;
03
解题关键是找出球心、半径与其它线面关系;
04
熟悉常见模型,将空间问题平面化.
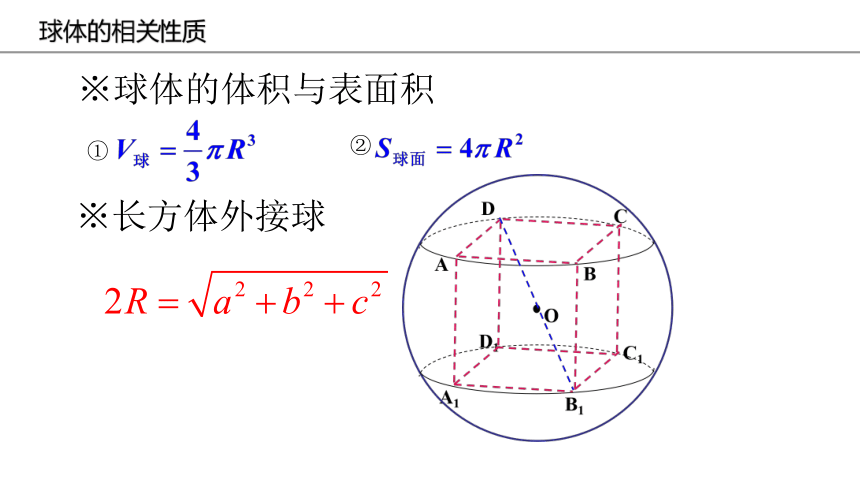
※球体的体积与表面积
①
②
※长方体外接球
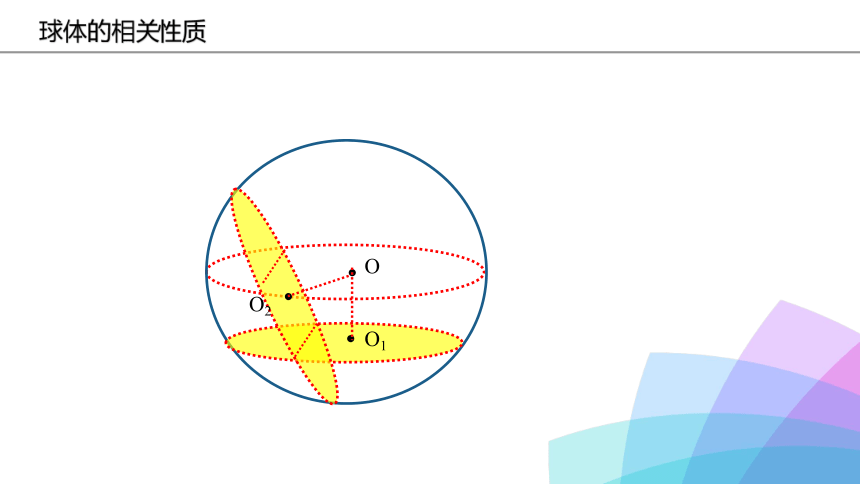
球体的相关性质
O
O1
O2
球体的相关性质
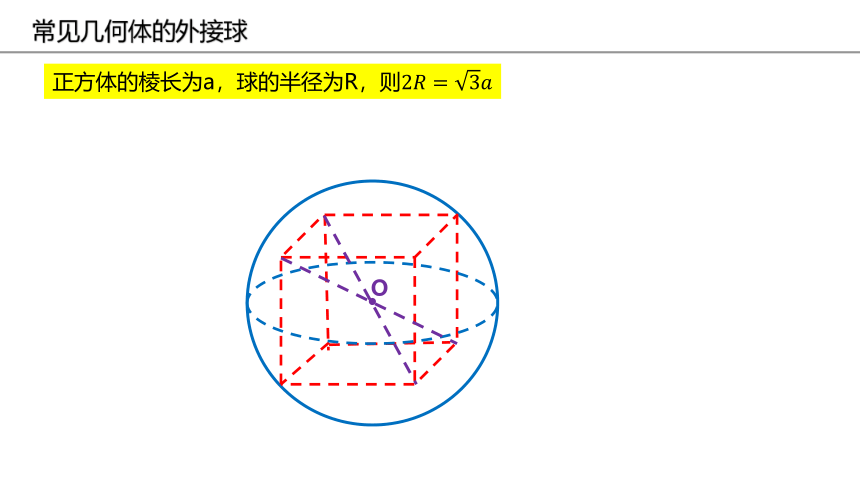
常见几何体的外接球
定义1:若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。
定义2:若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球.
常见几何体的外接球
正方体的棱长为a,球的半径为R,则
O
常见几何体的外接球
O
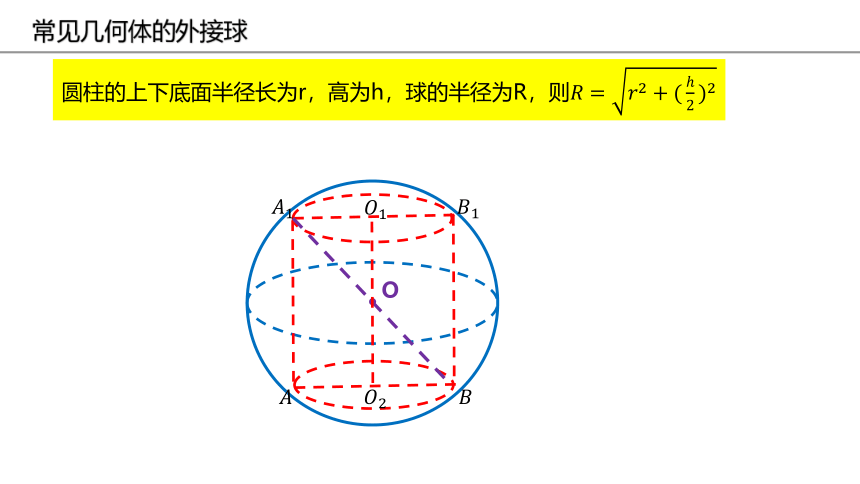
圆柱的上下底面半径长为r,高为h,球的半径为R,则
常见几何体的外接球
O
O1
A
B
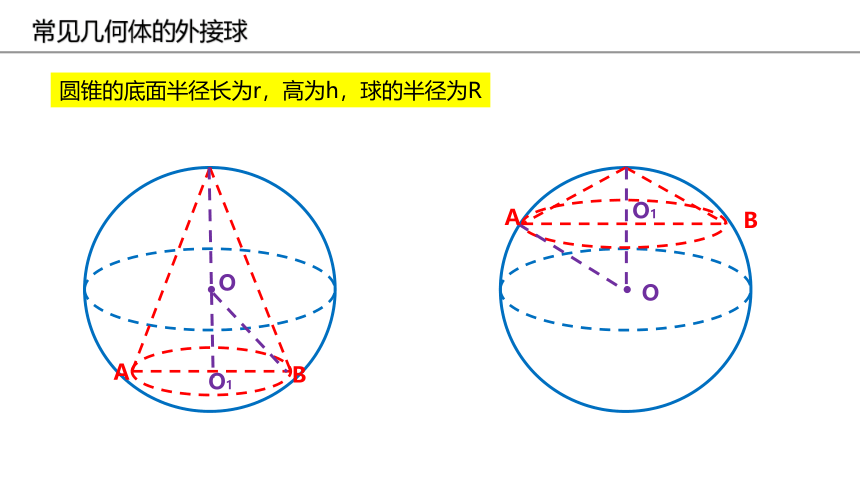
圆锥的底面半径长为r,高为h,球的半径为R
O
O1
A
B
常见几何体的外接球
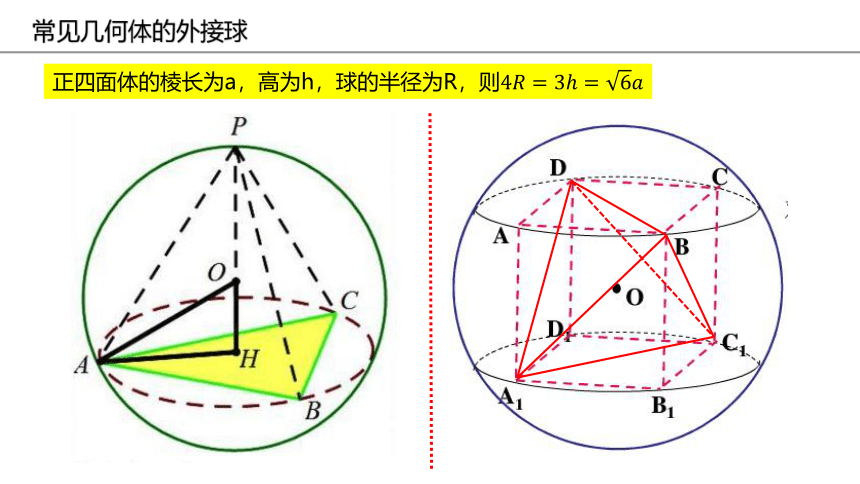
正四面体的棱长为a,高为h,球的半径为R,则
“墙角”模型
C
A
A1
B1
C1
D1
D
C
B
O2
O1
O
“墙角”模型
“墙角”模型
例1 [2019·全国卷Ⅰ] 已知三棱锥P-ABC的四个顶点在球O的球面,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为( )
A.8π B.4π C.2π D.π
思考?
“对棱相等”模型
例2
对棱相等,补全为长方体
“对棱相等”模型
“汉堡”模型
“汉堡”模型
例3 [2021·石家庄质检] 已知直三棱柱ABC-A1B1C1的底面ABC为等边三角形,若该三棱柱存在外接球与内切球,则其外接球与内切球的表面积之比为( )
A.25∶1 B.1∶25 C.1∶5 D.5∶1
“心有所依”模型
例4 [2020·十堰6月调研] 已知三棱锥M-ABC的四个顶点均在表面积为32π的球面上,AB=BC=2,AC=4,则三棱锥M-ABC的体积的最大值为( )
A.8 B.4+4 C. D.
M
“心有所依”模型
B
A
C
D
E
F
16π
P
D
C
A
B
O2
O1
O
“双心”模型
A
P
B
C
15π
“双心”模型
变式2
3
D
A
B
C
21π
O
O2
M
O1
O1
O
M
O2
“双心”模型
思考?
“双心”模型
“等体积法”模型
例6 [2020·福州质检] 在三棱锥P-ABC中,顶点P在底面ABC上的射影为△ABC的内心,三个侧面的面积分别为12,16,20,且底面面积为24,则三棱锥P-ABC的内切球的表面积为 ( )
A. B.12π C. D.16π
分析:由于三棱锥的内切球球心到各个面的距离是相等的,可以利用等体积法求半径,适用于球心不易找到的类型。
链接高考
1.
链接高考
链接高考
2.(2020·全国Ⅰ)已知A,B,C为球O的球面上的三个点,⊙O1为△ABC的外接圆.若⊙O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为( ) A.64π B.48π C.36π D.32π
当堂检测
B
B
D
请批评指正!
微专题:
空间几何体的外接球
厦门六中 郭祯
2015
2017
2018
2019
2020
感悟高考
延迟符
近几年新课标全国卷空间几何体外接球试题在题型、考查载体、考查能力、解题方法等方面呈现怎样的特征
01
考查以选择、填空题形式;难度中等;
02
载体以柱体、锥体为主,对空间想象能力要求较高;
03
解题关键是找出球心、半径与其它线面关系;
04
熟悉常见模型,将空间问题平面化.
※球体的体积与表面积
①
②
※长方体外接球
球体的相关性质
O
O1
O2
球体的相关性质
常见几何体的外接球
定义1:若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。
定义2:若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球.
常见几何体的外接球
正方体的棱长为a,球的半径为R,则
O
常见几何体的外接球
O
圆柱的上下底面半径长为r,高为h,球的半径为R,则
常见几何体的外接球
O
O1
A
B
圆锥的底面半径长为r,高为h,球的半径为R
O
O1
A
B
常见几何体的外接球
正四面体的棱长为a,高为h,球的半径为R,则
“墙角”模型
C
A
A1
B1
C1
D1
D
C
B
O2
O1
O
“墙角”模型
“墙角”模型
例1 [2019·全国卷Ⅰ] 已知三棱锥P-ABC的四个顶点在球O的球面,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为( )
A.8π B.4π C.2π D.π
思考?
“对棱相等”模型
例2
对棱相等,补全为长方体
“对棱相等”模型
“汉堡”模型
“汉堡”模型
例3 [2021·石家庄质检] 已知直三棱柱ABC-A1B1C1的底面ABC为等边三角形,若该三棱柱存在外接球与内切球,则其外接球与内切球的表面积之比为( )
A.25∶1 B.1∶25 C.1∶5 D.5∶1
“心有所依”模型
例4 [2020·十堰6月调研] 已知三棱锥M-ABC的四个顶点均在表面积为32π的球面上,AB=BC=2,AC=4,则三棱锥M-ABC的体积的最大值为( )
A.8 B.4+4 C. D.
M
“心有所依”模型
B
A
C
D
E
F
16π
P
D
C
A
B
O2
O1
O
“双心”模型
A
P
B
C
15π
“双心”模型
变式2
3
D
A
B
C
21π
O
O2
M
O1
O1
O
M
O2
“双心”模型
思考?
“双心”模型
“等体积法”模型
例6 [2020·福州质检] 在三棱锥P-ABC中,顶点P在底面ABC上的射影为△ABC的内心,三个侧面的面积分别为12,16,20,且底面面积为24,则三棱锥P-ABC的内切球的表面积为 ( )
A. B.12π C. D.16π
分析:由于三棱锥的内切球球心到各个面的距离是相等的,可以利用等体积法求半径,适用于球心不易找到的类型。
链接高考
1.
链接高考
链接高考
2.(2020·全国Ⅰ)已知A,B,C为球O的球面上的三个点,⊙O1为△ABC的外接圆.若⊙O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为( ) A.64π B.48π C.36π D.32π
当堂检测
B
B
D
请批评指正!
同课章节目录
