2022届高考数学二轮复习专题-点到平面的距离课件(共17张PPT)
文档属性
| 名称 | 2022届高考数学二轮复习专题-点到平面的距离课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-19 20:52:02 | ||
图片预览

文档简介
(共17张PPT)
点到平面的距离
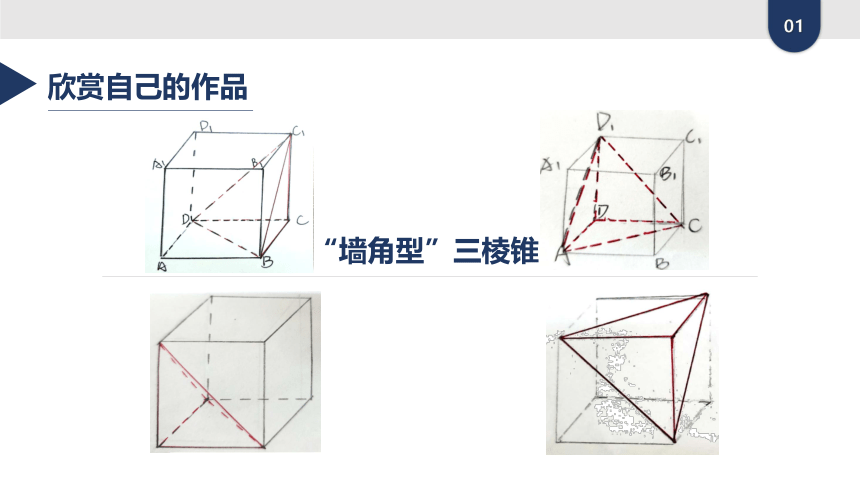
欣赏自己的作品
01
“墙角型”三棱锥
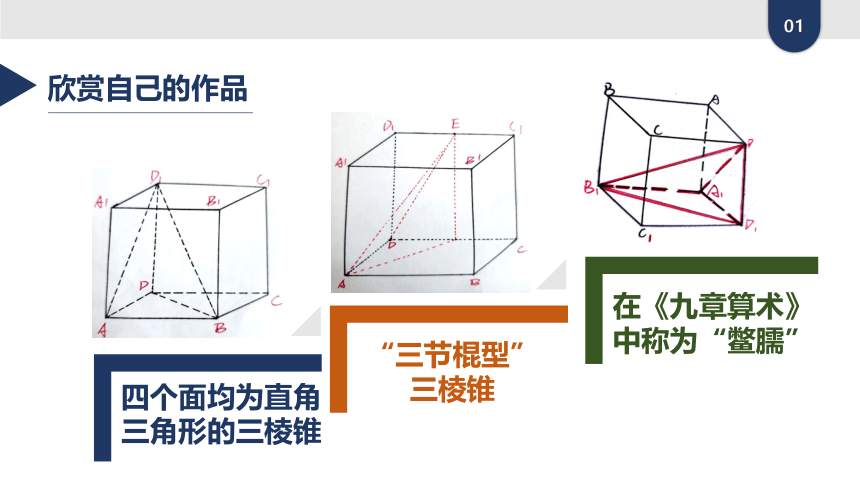
欣赏自己的作品
01
在《九章算术》
中称为“鳖臑”
四个面均为直角
三角形的三棱锥
“三节棍型”
三棱锥
01
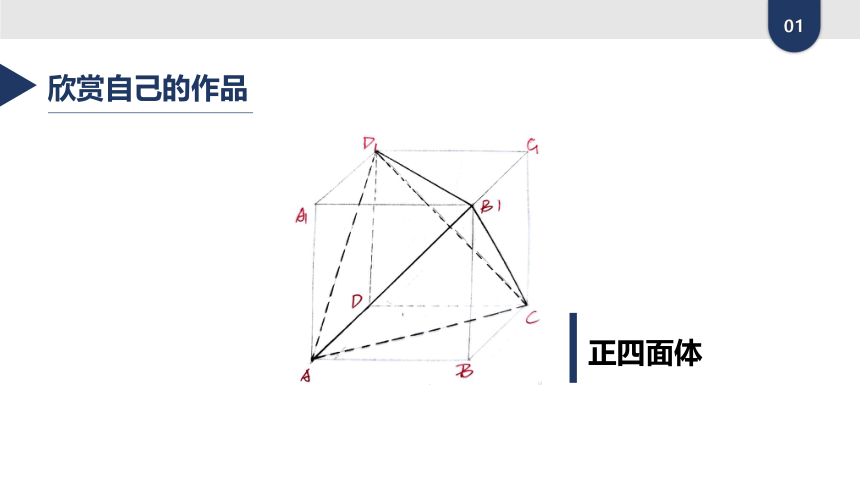
正四面体
欣赏自己的作品
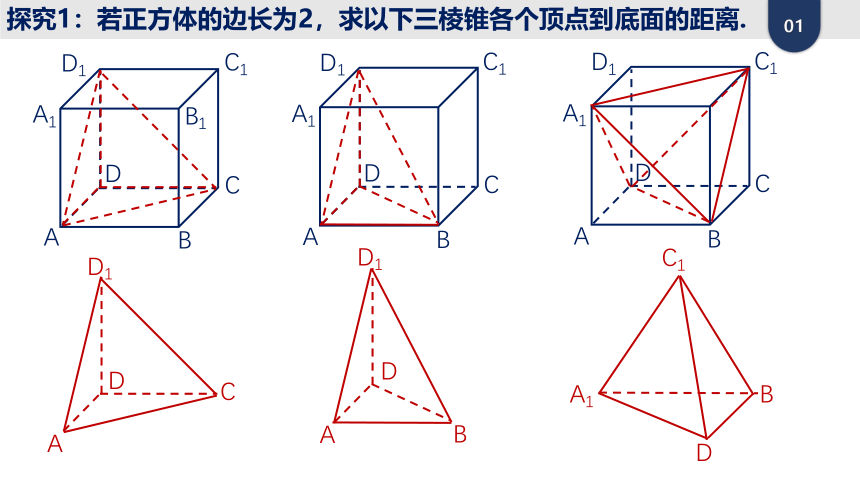
探究1:若正方体的边长为2,求以下三棱锥各个顶点到底面的距离.
01
A
B
C
D
A1
B1
C1
D1
A
C
D
D1
A
B
C
D
A1
C1
D1
A
B
D
D1
A
B
C
D
A1
C1
D1
C1
A1
D
B
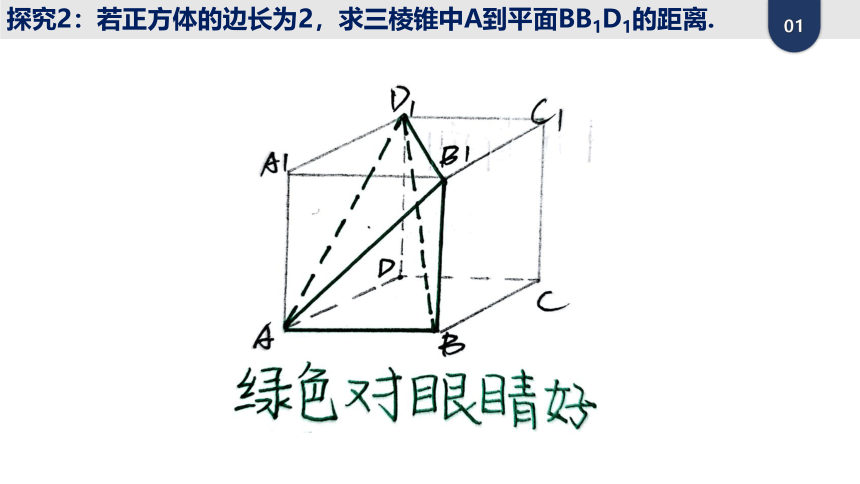
探究2:若正方体的边长为2,求三棱锥中A到平面BB1D1的距离.
01
02
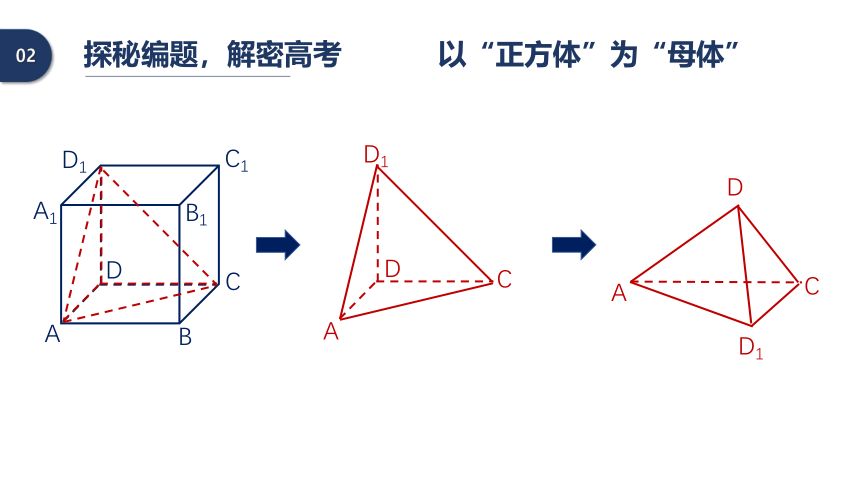
探秘编题,解密高考
以“正方体”为“母体”
A
B
C
D
A1
B1
C1
D1
A
C
D
D1
D
A
D1
C
02
探秘编题,解密高考
P
A
B
C
O
M
02
探秘编题,解密高考
如图,在三棱锥 P﹣ABC 中,AB=BC=2 ,PA=PB=PC=AC=4,O 为 AC 的中点.
(1)证明:PO⊥平面 ABC;
(2)若点 M 在棱 BC 上,且 MC=2MB,
求点 C 到平面 POM 的距离.
(2018年全国卷Ⅱ)
02
探秘编题,解密高考
02
探秘编题,解密高考
P
A
B
C
D
02
探秘编题,解密高考
(2017年全国卷Ⅱ)
如图,四棱锥 P﹣ABCD 中,侧面 PAD 为等边三角形且垂直于底面 ABCD,
AB = BC = AD,∠BAD =∠ABC = 90°.
(1)证明:直线 BC∥ 平面 PAD;
(2)若 △PCD 面积为 2,求四棱锥 P﹣ABCD 的体积.
02
探秘编题,解密高考
P
A
B
C
D
02
探秘编题,解密高考
(2017年全国卷Ⅰ )
如图,在四棱锥 P﹣ABCD 中,AB∥CD,且 ∠BAP =∠CDP = 90°.
(1)证明:平面 PAB⊥平面 PAD;
(2)若 PA=PD=AB=DC,∠APD=90°,且四棱锥 P﹣ABCD 的体积为 ,求该四棱锥的侧面积.
02
探秘编题,解密高考
E
A
B
C
D
02
探秘编题,解密高考
(2017年全国卷Ⅲ )
如图四面体 ABCD 中,△ABC 是正三角形,AD=CD.(1)证明:AC⊥BD;
(2)已知 △ACD 是直角三角形,AB=BD,若 E 为棱 BD 上与 D 不重合的点,且AE⊥EC,求四面体 ABCE 与四面体 ACDE 的体积比.
谢谢聆听
Thanks
点到平面的距离
欣赏自己的作品
01
“墙角型”三棱锥
欣赏自己的作品
01
在《九章算术》
中称为“鳖臑”
四个面均为直角
三角形的三棱锥
“三节棍型”
三棱锥
01
正四面体
欣赏自己的作品
探究1:若正方体的边长为2,求以下三棱锥各个顶点到底面的距离.
01
A
B
C
D
A1
B1
C1
D1
A
C
D
D1
A
B
C
D
A1
C1
D1
A
B
D
D1
A
B
C
D
A1
C1
D1
C1
A1
D
B
探究2:若正方体的边长为2,求三棱锥中A到平面BB1D1的距离.
01
02
探秘编题,解密高考
以“正方体”为“母体”
A
B
C
D
A1
B1
C1
D1
A
C
D
D1
D
A
D1
C
02
探秘编题,解密高考
P
A
B
C
O
M
02
探秘编题,解密高考
如图,在三棱锥 P﹣ABC 中,AB=BC=2 ,PA=PB=PC=AC=4,O 为 AC 的中点.
(1)证明:PO⊥平面 ABC;
(2)若点 M 在棱 BC 上,且 MC=2MB,
求点 C 到平面 POM 的距离.
(2018年全国卷Ⅱ)
02
探秘编题,解密高考
02
探秘编题,解密高考
P
A
B
C
D
02
探秘编题,解密高考
(2017年全国卷Ⅱ)
如图,四棱锥 P﹣ABCD 中,侧面 PAD 为等边三角形且垂直于底面 ABCD,
AB = BC = AD,∠BAD =∠ABC = 90°.
(1)证明:直线 BC∥ 平面 PAD;
(2)若 △PCD 面积为 2,求四棱锥 P﹣ABCD 的体积.
02
探秘编题,解密高考
P
A
B
C
D
02
探秘编题,解密高考
(2017年全国卷Ⅰ )
如图,在四棱锥 P﹣ABCD 中,AB∥CD,且 ∠BAP =∠CDP = 90°.
(1)证明:平面 PAB⊥平面 PAD;
(2)若 PA=PD=AB=DC,∠APD=90°,且四棱锥 P﹣ABCD 的体积为 ,求该四棱锥的侧面积.
02
探秘编题,解密高考
E
A
B
C
D
02
探秘编题,解密高考
(2017年全国卷Ⅲ )
如图四面体 ABCD 中,△ABC 是正三角形,AD=CD.(1)证明:AC⊥BD;
(2)已知 △ACD 是直角三角形,AB=BD,若 E 为棱 BD 上与 D 不重合的点,且AE⊥EC,求四面体 ABCE 与四面体 ACDE 的体积比.
谢谢聆听
Thanks
同课章节目录
