人教版新高考数学二轮复习课件--专项突破二 三角函数与解三角形解答题
文档属性
| 名称 | 人教版新高考数学二轮复习课件--专项突破二 三角函数与解三角形解答题 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 14:09:11 | ||
图片预览











文档简介
(共51张PPT)
专项突破二 三角函数与解三角形解答题
专题二
2022
高中总复习优化设计
GAO ZHONG ZONG FU XI YOU HUA SHE JI
内容索引
01
02
必备知识 精要梳理
关键能力 学案突破
必备知识 精要梳理
1.“五点法”作函数y=Asin(ωx+φ)(Aω≠0)的图象
2.确定函数y=Asin(ωx+φ)(A>0,ω>0)单调区间的方法
采用“换元”法整体代换,将“ωx+φ”看作一个整体,令“z=ωx+φ”,即通过求y=Asin z的单调区间而得到原函数的单调区间.
温馨提示若ω<0,可利用诱导公式先将x的系数转变为正数,再求单调区间.
3.求函数y=Asin(ωx+φ)(A>0,ω>0)最值的方法
(1)若x∈R,则当ωx+φ=2kπ+ (k∈Z)时函数取得最大值A,当ωx+φ=2kπ- (k∈Z)时函数取得最小值-A.
(2)若x∈[a,b],则应首先确定ωx+φ的取值区间,再根据正弦函数的性质求得函数的最值.
误区警示当x∈[a,b]时,函数y=Asin(ωx+φ)(A>0,ω>0)的最值不一定在区间的端点处取得,直接将端点值代入求得最值是错误的.
4.正弦定理、余弦定理及其变形
在△ABC中,内角A,B,C所对的边分别为a,b,c.
不能推出△ABC是锐角三角形
关键能力 学案突破
考向一
三角函数的图象与性质
命题角度1 三角函数的图象
(1)求函数f(x)的最大值,并求使f(x)取得最大值的x的取值集合;
(2)设函数h(x)=f(x)-g(x),画出h(x)在区间[0,π]上的图象.
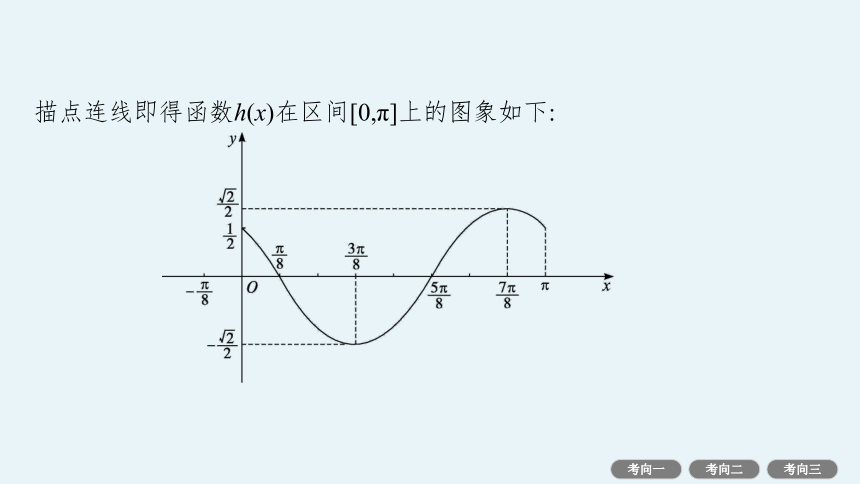
描点连线即得函数h(x)在区间[0,π]上的图象如下:
名师点析五点作图法注意点
利用五点作图法画函数f(x)=Asin(ωx+φ)(Aω≠0)在一个周期上的图象时,如果不指定具体的区间,则可由ωx+φ=0,2π确定区间的两个端点,画出一个周期上的图象;如果指定了区间,则除了找出位于该区间内的关键点以外,还要把区间的端点也要列在表格中,然后通过描点、连线,得到函数在该区间上的一段图象.
精典对练 得高分
(1)求函数f(x)的解析式;
(2)已知函数f(x)的图象上的三点M,N,P的横坐标分别为-1,1,5,求sin∠MNP的值.
解 (1)由题图可知,A=1,最小正周期T=4×2=8.
命题角度2 三角函数的性质
方法技巧求函数y=Asin(ωx+φ)(A>0,ω>0)在区间[a,b]上的最值和值域时,应先求出当x∈[a,b]时,ωx+φ的取值范围,然后再结合正弦函数的图象及性质求出函数y=Asin(ωx+φ)(A>0,ω>0)在区间[a,b]上的最值和值域.
精典对练 得高分
(2021·浙江,18)设函数f(x)=sin x+cos x(x∈R).
易错防范 不丢分
易错警示函数y=Asin(ωx+φ)+h(Aω≠0)的单调区间及最值求解易错提醒
(1)求函数y=Asin(ωx+φ)+h(Aω≠0)的单调区间时,主要利用整体换元思想,但应注意:①当自变量x的系数ω<0时,应先利用诱导公式,将系数化为正数,才能进行求解,否则易导致错解.②在y=Asin(ωx+φ)+h(Aω≠0)中,如果A<0,则原函数的单调区间与函数y=sin(ωx+φ)的单调区间恰好相反,应注意转换.
(2)求函数y=Asin(ωx+φ)+h(Aω≠0)在闭区间[a,b]上的最值时,一方面不能错误地认为y=sin(ωx+φ)的最大值和最小值就是1和-1,也不能认为最值一定在区间端点a,b处取得,而应该依据x∈[a,b]求出ωx+φ的取值区间,然后结合正弦函数的性质来确定函数的最值以及取得最值时自变量的值.
考向二
利用正弦定理、余弦定理解三角形
[例2](2021·新高考Ⅰ,19)记△ABC的内角A,B,C的对边分别为a,b,c.已知b2=ac,点D在边AC上,BDsin∠ABC=asin C.
(1)证明:BD=b;
(2)若AD=2DC,求cos∠ABC.
方法技巧解三角形问题的基本策略
(1)选定理.
①已知两角及一边,求其余的边或角,利用正弦定理.
②已知两边及其一边的对角,求另一边所对的角,利用正弦定理.
③已知两边及其夹角,求第三边,利用余弦定理.
④已知三边求角或角的余弦值,利用余弦定理的推论.
⑤已知两边及其一边的对角,求另一边,利用余弦定理.
(2)巧转化.化边为角后一般要结合三角形的内角和定理与三角恒等变换进行转化;若将条件转化为边之间的关系,则式子一般比较复杂,要注意根据式子结构特征灵活化简.
(3)得结论.利用三角函数公式,结合三角形的有关性质(如大边对大角,三角形的内角取值范围等),并注意利用数形结合求出三角形的边、角或判断出三角形的形状等.
精典对练 得高分
(1)求cos∠BDC;
(2)求BC的长.
一题多解 练思维
所以(x+y)2≤64,当且仅当x=y=4时等号成立,即(x+y)max=8,所以(AB+AD+BD)max=8+4=12,故△ABD周长的最大值为12.
方法技巧在已知三角形的一边及其对角的前提下,求该三角形周长或面积的最值通常有两种方法
(1)代数变换法:先利用余弦定理,建立三角形中未知的两条边满足的条件等式,然后利用基本不等式求出两边之和或两边之积的最值,最后结合周长公式或面积公式即得三角形周长或面积的最值.
(2)三角变换法:先利用正弦定理,建立三角形中未知的两条边和两角满足的关系式,并用其中的一个角表示两条边,然后根据周长公式或面积公式建立周长或面积关于该角的函数关系式,最后通过三角恒等变换对函数解析式进行化简,即可求得周长或面积的最值.
考向三
三角函数的实际应用
[例3](2021·吉林长春月考)如图,某污水处理厂要在一个矩形污水处理池ABCD的池底水平铺设污水净化管道(Rt△FHE三条边,H是直角顶点)来处理污水,管道越长,污水净化效果越好.要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上,已知AB=20米,AD=10 米,记∠BHE=θ.
(1)试将污水净化管道的总长度L(即Rt△FHE的周长)表示为θ的函数,并求出定义域;
(2)问当θ取何值时,污水净化效果最好 并求出此时
管道的总长度.
方法点拨利用三角函数解决实际应用问题的方法步骤
(1)分析理解题意,弄清已知与未知,抽象出一个或几个三角形.
(2)根据已知条件与求解目标,建立三角函数模型.
(3)根据正弦定理、余弦定理以及三角恒等变换等方法解决三角函数问题.
(4)得到原实际问题的解.
精典对练 得高分
(2021·山东青岛一模)如图,在△ABC中,AB⊥AC,AB=AC=2,点E,F是线段BC(含端点)上的动点,且点E在点F的右下方,在运动的过程中,始终保持∠EAF= 不变,设∠EAB=θ.
(1)写出θ的取值范围,并分别求出线段AE,AF关于θ的函数关系式;
(2)求△EAF面积S的最小值.
专项突破二 三角函数与解三角形解答题
专题二
2022
高中总复习优化设计
GAO ZHONG ZONG FU XI YOU HUA SHE JI
内容索引
01
02
必备知识 精要梳理
关键能力 学案突破
必备知识 精要梳理
1.“五点法”作函数y=Asin(ωx+φ)(Aω≠0)的图象
2.确定函数y=Asin(ωx+φ)(A>0,ω>0)单调区间的方法
采用“换元”法整体代换,将“ωx+φ”看作一个整体,令“z=ωx+φ”,即通过求y=Asin z的单调区间而得到原函数的单调区间.
温馨提示若ω<0,可利用诱导公式先将x的系数转变为正数,再求单调区间.
3.求函数y=Asin(ωx+φ)(A>0,ω>0)最值的方法
(1)若x∈R,则当ωx+φ=2kπ+ (k∈Z)时函数取得最大值A,当ωx+φ=2kπ- (k∈Z)时函数取得最小值-A.
(2)若x∈[a,b],则应首先确定ωx+φ的取值区间,再根据正弦函数的性质求得函数的最值.
误区警示当x∈[a,b]时,函数y=Asin(ωx+φ)(A>0,ω>0)的最值不一定在区间的端点处取得,直接将端点值代入求得最值是错误的.
4.正弦定理、余弦定理及其变形
在△ABC中,内角A,B,C所对的边分别为a,b,c.
不能推出△ABC是锐角三角形
关键能力 学案突破
考向一
三角函数的图象与性质
命题角度1 三角函数的图象
(1)求函数f(x)的最大值,并求使f(x)取得最大值的x的取值集合;
(2)设函数h(x)=f(x)-g(x),画出h(x)在区间[0,π]上的图象.
描点连线即得函数h(x)在区间[0,π]上的图象如下:
名师点析五点作图法注意点
利用五点作图法画函数f(x)=Asin(ωx+φ)(Aω≠0)在一个周期上的图象时,如果不指定具体的区间,则可由ωx+φ=0,2π确定区间的两个端点,画出一个周期上的图象;如果指定了区间,则除了找出位于该区间内的关键点以外,还要把区间的端点也要列在表格中,然后通过描点、连线,得到函数在该区间上的一段图象.
精典对练 得高分
(1)求函数f(x)的解析式;
(2)已知函数f(x)的图象上的三点M,N,P的横坐标分别为-1,1,5,求sin∠MNP的值.
解 (1)由题图可知,A=1,最小正周期T=4×2=8.
命题角度2 三角函数的性质
方法技巧求函数y=Asin(ωx+φ)(A>0,ω>0)在区间[a,b]上的最值和值域时,应先求出当x∈[a,b]时,ωx+φ的取值范围,然后再结合正弦函数的图象及性质求出函数y=Asin(ωx+φ)(A>0,ω>0)在区间[a,b]上的最值和值域.
精典对练 得高分
(2021·浙江,18)设函数f(x)=sin x+cos x(x∈R).
易错防范 不丢分
易错警示函数y=Asin(ωx+φ)+h(Aω≠0)的单调区间及最值求解易错提醒
(1)求函数y=Asin(ωx+φ)+h(Aω≠0)的单调区间时,主要利用整体换元思想,但应注意:①当自变量x的系数ω<0时,应先利用诱导公式,将系数化为正数,才能进行求解,否则易导致错解.②在y=Asin(ωx+φ)+h(Aω≠0)中,如果A<0,则原函数的单调区间与函数y=sin(ωx+φ)的单调区间恰好相反,应注意转换.
(2)求函数y=Asin(ωx+φ)+h(Aω≠0)在闭区间[a,b]上的最值时,一方面不能错误地认为y=sin(ωx+φ)的最大值和最小值就是1和-1,也不能认为最值一定在区间端点a,b处取得,而应该依据x∈[a,b]求出ωx+φ的取值区间,然后结合正弦函数的性质来确定函数的最值以及取得最值时自变量的值.
考向二
利用正弦定理、余弦定理解三角形
[例2](2021·新高考Ⅰ,19)记△ABC的内角A,B,C的对边分别为a,b,c.已知b2=ac,点D在边AC上,BDsin∠ABC=asin C.
(1)证明:BD=b;
(2)若AD=2DC,求cos∠ABC.
方法技巧解三角形问题的基本策略
(1)选定理.
①已知两角及一边,求其余的边或角,利用正弦定理.
②已知两边及其一边的对角,求另一边所对的角,利用正弦定理.
③已知两边及其夹角,求第三边,利用余弦定理.
④已知三边求角或角的余弦值,利用余弦定理的推论.
⑤已知两边及其一边的对角,求另一边,利用余弦定理.
(2)巧转化.化边为角后一般要结合三角形的内角和定理与三角恒等变换进行转化;若将条件转化为边之间的关系,则式子一般比较复杂,要注意根据式子结构特征灵活化简.
(3)得结论.利用三角函数公式,结合三角形的有关性质(如大边对大角,三角形的内角取值范围等),并注意利用数形结合求出三角形的边、角或判断出三角形的形状等.
精典对练 得高分
(1)求cos∠BDC;
(2)求BC的长.
一题多解 练思维
所以(x+y)2≤64,当且仅当x=y=4时等号成立,即(x+y)max=8,所以(AB+AD+BD)max=8+4=12,故△ABD周长的最大值为12.
方法技巧在已知三角形的一边及其对角的前提下,求该三角形周长或面积的最值通常有两种方法
(1)代数变换法:先利用余弦定理,建立三角形中未知的两条边满足的条件等式,然后利用基本不等式求出两边之和或两边之积的最值,最后结合周长公式或面积公式即得三角形周长或面积的最值.
(2)三角变换法:先利用正弦定理,建立三角形中未知的两条边和两角满足的关系式,并用其中的一个角表示两条边,然后根据周长公式或面积公式建立周长或面积关于该角的函数关系式,最后通过三角恒等变换对函数解析式进行化简,即可求得周长或面积的最值.
考向三
三角函数的实际应用
[例3](2021·吉林长春月考)如图,某污水处理厂要在一个矩形污水处理池ABCD的池底水平铺设污水净化管道(Rt△FHE三条边,H是直角顶点)来处理污水,管道越长,污水净化效果越好.要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上,已知AB=20米,AD=10 米,记∠BHE=θ.
(1)试将污水净化管道的总长度L(即Rt△FHE的周长)表示为θ的函数,并求出定义域;
(2)问当θ取何值时,污水净化效果最好 并求出此时
管道的总长度.
方法点拨利用三角函数解决实际应用问题的方法步骤
(1)分析理解题意,弄清已知与未知,抽象出一个或几个三角形.
(2)根据已知条件与求解目标,建立三角函数模型.
(3)根据正弦定理、余弦定理以及三角恒等变换等方法解决三角函数问题.
(4)得到原实际问题的解.
精典对练 得高分
(2021·山东青岛一模)如图,在△ABC中,AB⊥AC,AB=AC=2,点E,F是线段BC(含端点)上的动点,且点E在点F的右下方,在运动的过程中,始终保持∠EAF= 不变,设∠EAB=θ.
(1)写出θ的取值范围,并分别求出线段AE,AF关于θ的函数关系式;
(2)求△EAF面积S的最小值.
同课章节目录
