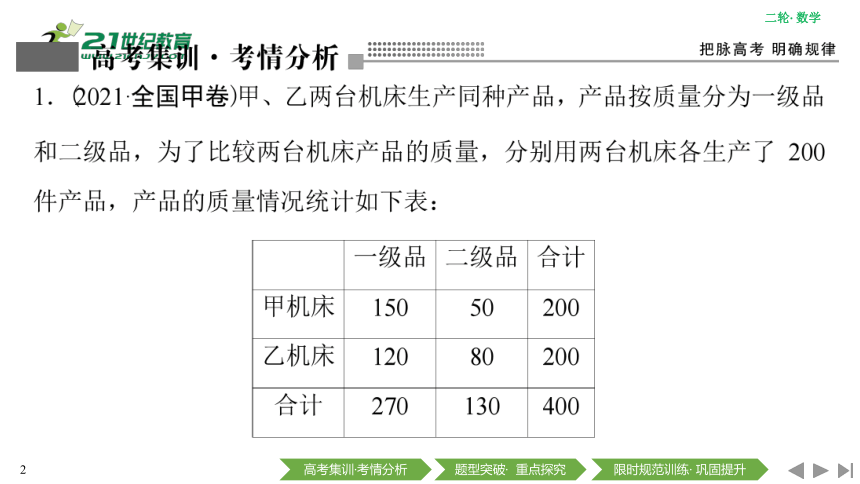
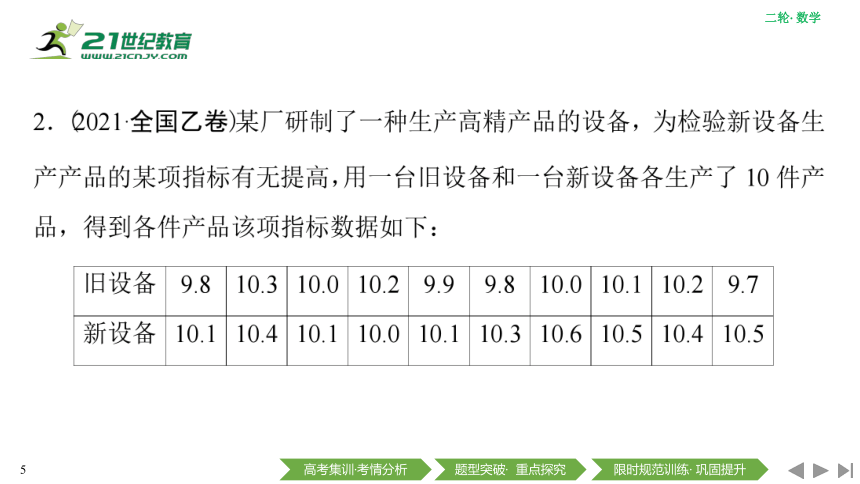
13概率与统计——2022高考数学二轮复习课件
文档属性
| 名称 | 13概率与统计——2022高考数学二轮复习课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 16:02:19 | ||
图片预览










文档简介
(共98张PPT)
13概率与统计
二轮复习
.
(1)求甲连胜四场的概率;
(2)求需要进行第五场比赛的概率;
(3)求丙最终获胜的概率.
(3)分层抽样:根据植物覆盖面积的大小对地块分层,再对200个地块进行分层抽样.
理由如下:由(2)知各样区的这种野生动物数量与植物覆盖面积有很强的正相关.由于各地块间植物覆盖面积差异很大,从而各地块间这种野生动物数量差异也很大,采用分层抽样的方法较好地保持了样本结构与总体结构的一致性,提高了样本的代表性,从而可以获得该地区这种野生动物数量更准确的估计.
5.(2020·全国卷Ⅲ)某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位:天):
锻炼人次
空气质量等级 [0,200] (200,400] (400,600]
1(优) 2 16 25
2(良) 5 10 12
3(轻度污染) 6 7 8
4(中度污染) 7 2 0
(1)分别估计该市一天的空气质量等级为1,2,3,4的概率;
(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);
(3)若某天的空气质量等级为1或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关?
.
6.(2019·全国卷Ⅰ)为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得-1分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.
[把脉考情]
考什么 1.相互独立事件、独立重复试验概率的求法.
2.离散型随机变量的均值与方差的求法.
3.二项分布与正态分布的应用.
4.与回归分析、独立性检验交汇考查.
新动向 以社会热点话题为背景,结合“五育并举”要求在解答题中继续考查概率与统计的综合问题,注意近两年综合性、交汇性加强,难度增大.
年份 2010 2011 2012 2013 2014 2015 2016 2017 2018
年生产量(万台) 3 4 5 6 7 7 9 10 12
产品年利
润(千万元) 3.6 4.1 4.4 5.2 6.2 7.8 7.5 7.9 9.1
年返修量(台) 47 42 48 50 92 83 72 87 90
(1)从该公司2010~2018年的相关数据中任意选取3年的数据,以X表示3年中生产部门获得考核优秀的次数,求X的分布列和数学期望;
(2)根据散点图发现2015年数据偏差较大,如果去掉该年的数据,试用剩下的数据求出年利润y(千万元)关于年生产量x(万台)的线性回归方程
(精确到0.01).
破解概率与回归分析的综合问题的关键
(1)读准题目中的数据.
(2)学会对问题进行分析转化.
(3)熟练掌握求线性回归方程的步骤.
[即学即用]
(2021·云南师大附中月考)某项科研活动共进行了5次试验,其数据如表所示:
次数
特征量 第1次 第2次 第3次 第4次 第5次
x 2 5 8 9 11
y 12 10 8 8 7
(1)根据表中的数据,运用相关系数进行分析说明,是否可以用线性回归模型拟合y与x的关系,并指出是正相关还是负相关;
(2)求特征量y关于x的经验回归方程,并预测当特征量x为12时特征量y的值.
(1)完成2×2列联表,并回答能否有99%的把握认为“对线上教育是否满意与性别有关”;
满意 不满意 合计
男生
女生
合计 120
解决独立性检验与概率综合问题的步骤
(1)分析数据:根据条件中提供的数据准确分析数据.
(2)准确计算:对频率的计算或K2的计算确保计算准确.
(3)作出结论:用频率估计概率或根据K2的观测值与临界值进行对比时,注意问题的结论回答准确.
[即学即用]
(2021·沈阳铁路中学月考)司机在开机动车时使用手机是违法行为,会存在严重的安全隐患,危及自己和他人的生命.为了研究司机开车时使用手机的情况,交警部门调查了100名机动车司机,得到以下统计:在55名男性司机中,开车时使用手机的有40人,开车时不使用手机的有15人;在45名女性司机中,开车时使用手机的有20人,开车时不使用手机的有25人.
(1)完成下面的2×2列联表,并判断是否有99.5%的把握认为开车时使用手机与司机的性别有关;
开车时使用手机 开车时不使用手机 合计
男性司机人数
女性司机人数
合计
[学审题]
条件信息 想到方法 注意什么
信息 零件数X 利用正态分布、二项分布性质求解 (1)注意利用对立事件的概率求P(X≥1)
(2)注意3σ原则的应用
信息 给出生产过程可能出现异常情况的条件 利用独立性检验的思想判断监控生产过程方法的合理性
信息 利用估计值判断问题 确定μ-3σ,μ+3σ的取值,以剔除(μ-3σ,μ+3σ)之外的数据
解决正态分布问题有三个关键点
(1)对称轴x=μ.
(2)标准差σ.
(3)分布区间.利用对称性求指定范围内的概率值;由μ,σ分布区间的特征进行转化,使分布区间转化为3σ特殊区间,从而求出所求概率.
已知小明能正确回答A类问题的概率为0.8,能正确回答B类问题的概率为0.6,且能正确回答问题的概率与回答次序无关.
(1)若小明先回答A类问题,记X为小明的累计得分,求X的分布列;
(2)为使累计得分的期望最大,小明应选择先回答哪类问题?并说明理由.
[解析] (1)由题易知X的所有可能取值为0,20,100,
P(X=0)=1-0.8=0.2,
P(X=20)=0.8×(1-0.6)=0.32,
P(X=100)=0.8×0.6=0.48,
所以X的分布列为:
X 0 20 100
P 0.2 0.32 0.48
1.求解离散型随机变量的期望与方差的解题模型
2.期望与方差在优化决策中应用注意点
(1)若期望值差距较大,可用期望值得出结论.
(2)若期望值相同,可用方差得出结论,注意方差越小,波动性越小,较稳定.
[即学即用]
随着国内电商的不断发展,快递业也进入了高速发展时期,按照国务院的发展战略布局,以及国家邮政管理总局对快递业的宏观调控,某快递公司收取快递费的标准:质量不超过1 kg的包裹收费10元;质量超过1 kg的包裹,在收费10元的基础上,每超过1 kg(不足1 kg,按1 kg计算)需再收5元.某县该快递公司代办点将最近承揽的100件包裹的质量统计如下表:
质量(单位:kg) (0,1] (1,2] (2,3] (3,4] (4,5]
件数 43 30 15 8 4
(1)计算该代办点未来5天内不少于2天揽件数在101~300之间的概率;
(2)①估计该代办点对每件包裹收取的快递费的平均值;
②根据以往的经验,该代办点将快递费的三分之一作为前台工作人员的工资和利润,其余的用作其他费用.目前该代办点前台有工作人员3人,每人每天揽件不超过150件,日工资110元.代办点正在考虑是否将前台工作人员裁减1人,试计算裁员前后代办点每日利润的数学期望,若你是决策者,是否裁减工作人员1人?
https://www.21cnjy.com/help/help_extract.php
13概率与统计
二轮复习
.
(1)求甲连胜四场的概率;
(2)求需要进行第五场比赛的概率;
(3)求丙最终获胜的概率.
(3)分层抽样:根据植物覆盖面积的大小对地块分层,再对200个地块进行分层抽样.
理由如下:由(2)知各样区的这种野生动物数量与植物覆盖面积有很强的正相关.由于各地块间植物覆盖面积差异很大,从而各地块间这种野生动物数量差异也很大,采用分层抽样的方法较好地保持了样本结构与总体结构的一致性,提高了样本的代表性,从而可以获得该地区这种野生动物数量更准确的估计.
5.(2020·全国卷Ⅲ)某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位:天):
锻炼人次
空气质量等级 [0,200] (200,400] (400,600]
1(优) 2 16 25
2(良) 5 10 12
3(轻度污染) 6 7 8
4(中度污染) 7 2 0
(1)分别估计该市一天的空气质量等级为1,2,3,4的概率;
(2)求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);
(3)若某天的空气质量等级为1或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关?
.
6.(2019·全国卷Ⅰ)为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得-1分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.
[把脉考情]
考什么 1.相互独立事件、独立重复试验概率的求法.
2.离散型随机变量的均值与方差的求法.
3.二项分布与正态分布的应用.
4.与回归分析、独立性检验交汇考查.
新动向 以社会热点话题为背景,结合“五育并举”要求在解答题中继续考查概率与统计的综合问题,注意近两年综合性、交汇性加强,难度增大.
年份 2010 2011 2012 2013 2014 2015 2016 2017 2018
年生产量(万台) 3 4 5 6 7 7 9 10 12
产品年利
润(千万元) 3.6 4.1 4.4 5.2 6.2 7.8 7.5 7.9 9.1
年返修量(台) 47 42 48 50 92 83 72 87 90
(1)从该公司2010~2018年的相关数据中任意选取3年的数据,以X表示3年中生产部门获得考核优秀的次数,求X的分布列和数学期望;
(2)根据散点图发现2015年数据偏差较大,如果去掉该年的数据,试用剩下的数据求出年利润y(千万元)关于年生产量x(万台)的线性回归方程
(精确到0.01).
破解概率与回归分析的综合问题的关键
(1)读准题目中的数据.
(2)学会对问题进行分析转化.
(3)熟练掌握求线性回归方程的步骤.
[即学即用]
(2021·云南师大附中月考)某项科研活动共进行了5次试验,其数据如表所示:
次数
特征量 第1次 第2次 第3次 第4次 第5次
x 2 5 8 9 11
y 12 10 8 8 7
(1)根据表中的数据,运用相关系数进行分析说明,是否可以用线性回归模型拟合y与x的关系,并指出是正相关还是负相关;
(2)求特征量y关于x的经验回归方程,并预测当特征量x为12时特征量y的值.
(1)完成2×2列联表,并回答能否有99%的把握认为“对线上教育是否满意与性别有关”;
满意 不满意 合计
男生
女生
合计 120
解决独立性检验与概率综合问题的步骤
(1)分析数据:根据条件中提供的数据准确分析数据.
(2)准确计算:对频率的计算或K2的计算确保计算准确.
(3)作出结论:用频率估计概率或根据K2的观测值与临界值进行对比时,注意问题的结论回答准确.
[即学即用]
(2021·沈阳铁路中学月考)司机在开机动车时使用手机是违法行为,会存在严重的安全隐患,危及自己和他人的生命.为了研究司机开车时使用手机的情况,交警部门调查了100名机动车司机,得到以下统计:在55名男性司机中,开车时使用手机的有40人,开车时不使用手机的有15人;在45名女性司机中,开车时使用手机的有20人,开车时不使用手机的有25人.
(1)完成下面的2×2列联表,并判断是否有99.5%的把握认为开车时使用手机与司机的性别有关;
开车时使用手机 开车时不使用手机 合计
男性司机人数
女性司机人数
合计
[学审题]
条件信息 想到方法 注意什么
信息 零件数X 利用正态分布、二项分布性质求解 (1)注意利用对立事件的概率求P(X≥1)
(2)注意3σ原则的应用
信息 给出生产过程可能出现异常情况的条件 利用独立性检验的思想判断监控生产过程方法的合理性
信息 利用估计值判断问题 确定μ-3σ,μ+3σ的取值,以剔除(μ-3σ,μ+3σ)之外的数据
解决正态分布问题有三个关键点
(1)对称轴x=μ.
(2)标准差σ.
(3)分布区间.利用对称性求指定范围内的概率值;由μ,σ分布区间的特征进行转化,使分布区间转化为3σ特殊区间,从而求出所求概率.
已知小明能正确回答A类问题的概率为0.8,能正确回答B类问题的概率为0.6,且能正确回答问题的概率与回答次序无关.
(1)若小明先回答A类问题,记X为小明的累计得分,求X的分布列;
(2)为使累计得分的期望最大,小明应选择先回答哪类问题?并说明理由.
[解析] (1)由题易知X的所有可能取值为0,20,100,
P(X=0)=1-0.8=0.2,
P(X=20)=0.8×(1-0.6)=0.32,
P(X=100)=0.8×0.6=0.48,
所以X的分布列为:
X 0 20 100
P 0.2 0.32 0.48
1.求解离散型随机变量的期望与方差的解题模型
2.期望与方差在优化决策中应用注意点
(1)若期望值差距较大,可用期望值得出结论.
(2)若期望值相同,可用方差得出结论,注意方差越小,波动性越小,较稳定.
[即学即用]
随着国内电商的不断发展,快递业也进入了高速发展时期,按照国务院的发展战略布局,以及国家邮政管理总局对快递业的宏观调控,某快递公司收取快递费的标准:质量不超过1 kg的包裹收费10元;质量超过1 kg的包裹,在收费10元的基础上,每超过1 kg(不足1 kg,按1 kg计算)需再收5元.某县该快递公司代办点将最近承揽的100件包裹的质量统计如下表:
质量(单位:kg) (0,1] (1,2] (2,3] (3,4] (4,5]
件数 43 30 15 8 4
(1)计算该代办点未来5天内不少于2天揽件数在101~300之间的概率;
(2)①估计该代办点对每件包裹收取的快递费的平均值;
②根据以往的经验,该代办点将快递费的三分之一作为前台工作人员的工资和利润,其余的用作其他费用.目前该代办点前台有工作人员3人,每人每天揽件不超过150件,日工资110元.代办点正在考虑是否将前台工作人员裁减1人,试计算裁员前后代办点每日利润的数学期望,若你是决策者,是否裁减工作人员1人?
https://www.21cnjy.com/help/help_extract.php
同课章节目录
