12概率、统计、统计案例——2022高考数学二轮复习课件
文档属性
| 名称 | 12概率、统计、统计案例——2022高考数学二轮复习课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 16:02:19 | ||
图片预览










文档简介
(共71张PPT)
12概率、统计、统计案例
二轮复习
C
B
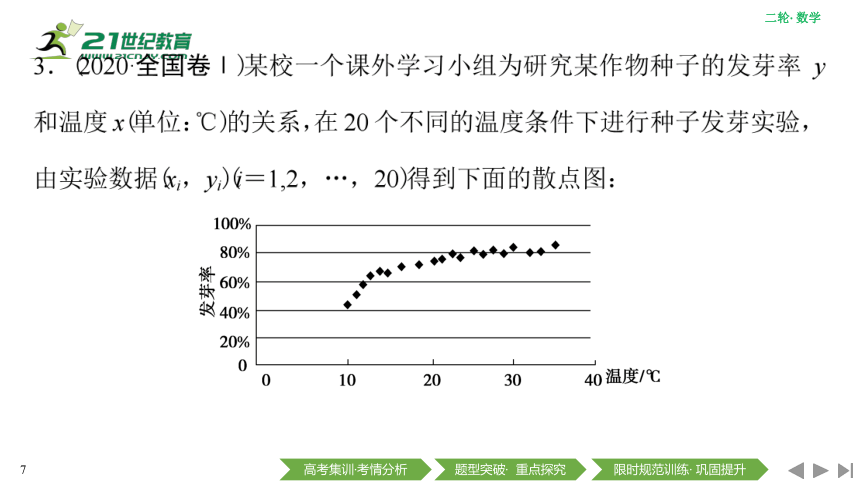
由此散点图,在10 ℃至40 ℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是( )
A.y=a+bx B.y=a+bx2
C.y=a+bex D.y=a+bln x
解析:由散点图可以看出,点大致分布在对数型函数的图象附近.
D
B
5.(2019·全国卷Ⅰ)某学校为了解1 000名新生的身体素质,将这些学生编号为1,2,…,1 000,从这些新生中用系统抽样方法等距抽取100名学生进行体质测验.若46号学生被抽到,则下面4名学生中被抽到的是( )
A.8号学生 B.200号学生
C.616号学生 D.815号学生
C
A
7.(2021·全国甲卷)为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
C
解析:由频率分布直方图可得,该地农户家庭年收入低于4.5万元和不低于10.5万元的频率分别为0.06和0.10,则农户比率分别为6%和10%,故A、B中结论正确;家庭年收入介于4.5万元和8.5万元之间的频率为0.10+0.14+0.20+0.20=0.64,故D中结论正确;
家庭年收入的平均值为0.02×3+0.04×4+0.10×5+0.14×6+0.20×7+0.20×8+0.10×9+0.10×10+0.04×11+0.02×12+0.02×13+0.02×14=7.68万元,因为7.68>6.5,所以估计该地区农户家庭年收入的平均值超过6.5万元,故C中结论不正确.
8.(2021·新高考全国Ⅰ卷)有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回地随机取两次,每次取1个球.甲表示事件“第一次取出的球的数字是1”,乙表示事件“第二次取出的球的数字是2”,丙表示事件“两次取出的球的数字之和是8”,丁表示事件“两次取出的球的数字之和是7”,则( )
A.甲与丙相互独立 B.甲与丁相互独立
C.乙与丙相互独立 D.丙与丁相互独立
B
9.(2019·全国卷Ⅰ)甲、乙两队进行篮球决赛,采取七场四胜制(当一队赢得四场胜利时,该队获胜,决赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主主客客主客主”.设甲队主场取胜的概率为0.6,客场取胜的概率为0.5,且各场比赛结果相互独立,则甲队以4∶1获胜的概率是________.
解析:甲队以4∶1获胜,甲队在第5场(主场)获胜,前4场中有一场输.
若在主场输一场,则概率为2×0.6×0.4×0.5×0.5×0.6;
若在客场输一场,则概率为2×0.6×0.6×0.5×0.5×0.6.
∴甲队以4∶1获胜的概率P=2×0.6×0.5×0.5×(0.6+0.4)×0.6=0.18.
答案:0.18
[把脉考情]
考什么 1.抽样方法(系统抽样、分层抽样)的应用.
2.古典概型与几何概型求法.
3.用样本估计总体的应用.
4.相互独立事件的概率,独立重复试验的应用.
新动向 1.在选择和填空题中继续考查抽样方法、用样本估计总体及概率的求法.
2.与概率交汇考查概率与统计的综合应用.
解析:由题意得,抽取的样本容量为(15 500+7 500+5 000)×4%=1 120,抽取的高中生参与家务劳动的人数为5 000×0.55×4%=110.
答案:C
C
3.(2021·重庆模拟)为了更好地支持中小型企业的发展,某市决定对部分企业的税收进行适当的减免,某机构调查了当地的中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,下面三个结论:
①样本数据落在区间[300,500)的频率为0.45;
②如果规定年收入在500万元以内的企业才能享受减免税收政策,估计有55%的当地中小型企业能享受到减免税收政策;
③样本的中位数为480万元.
其中正确结论的个数为( )
A.0 B.1
C.2 D.3
D
4.将甲、乙两个篮球队10场比赛的得分数据整理成如图所示的茎叶图,由图可知( )
A.甲队得分的众数是3
B.甲、乙两队得分在[30,39)分数段频率相等
C.甲、乙两队得分的极差相等
D.乙队得分的中位数是38.5
D
1.众数、中位数、平均数与直方图的关系
(1)众数为频率分布直方图中最高矩形的底边中点的横坐标.
(2)中位数为平分频率分布直方图面积且垂直于横轴的直线与横轴交点的横坐标.
(3)平均数等于频率分布直方图中每个小矩形的面积乘小矩形底边中点的横坐标之和.
2.方差的计算与含义
计算方差首先要计算平均数,再按照方差的计算公式进行计算,方差和标准差是描述一个样本和总体的波动大小的特征数,方差、标准差越大说明波动越大.
D
(2)(2021·黑龙江模拟)千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了所在地区A的100天日落情况和夜晚天气,得到如下2×2列联表,并计算得到K2≈19.05.下列小波对地区A的天气判断不正确的是( )
B
P(K2≥k) 0.050 0.010 0.001
k 3.841 6.635 10.828
,
A
C
A
A
B
1.古典概型概率的求解关键及注意点
(1)正确求出基本事件总数和所求概率事件包含的基本事件总数.
(2)对于较复杂的题目条件计数时要正确分类,分类时应不重不漏.
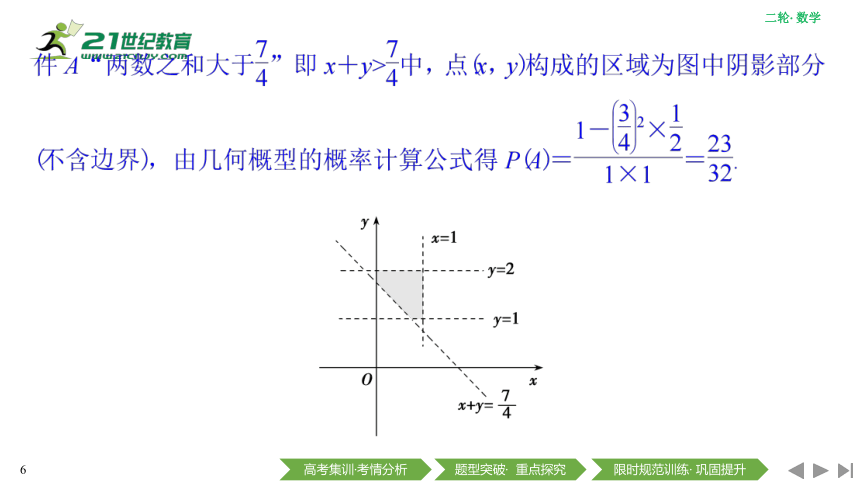
2.几何概型的适用条件及求解关键
(1)当构成试验的结果的区域为长度、面积、体积、弧长、夹角等时,应考虑使用几何概型求解.
(2)求解关键是寻找构成试验的全部结果的区域和事件发生的区域,有时需要设出变量,在坐标系中表示所需要的区域.
B
B
2.复杂事件概率的求法
(1)直接法:正确分析复杂事件的构成,求复杂事件转化为几个彼此互斥的事件的和事件或几个相互独立事件同时发生的积事件或一独立重复试验问题,然后用相应概率公式求解.
(2)间接法:当复杂事件正面情况比较多,反面情况较少时,则可利用其对立事件进行求解.对于“至少”“至多”等问题往往也用这种方法求解.
C
C
https://www.21cnjy.com/help/help_extract.php
12概率、统计、统计案例
二轮复习
C
B
由此散点图,在10 ℃至40 ℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是( )
A.y=a+bx B.y=a+bx2
C.y=a+bex D.y=a+bln x
解析:由散点图可以看出,点大致分布在对数型函数的图象附近.
D
B
5.(2019·全国卷Ⅰ)某学校为了解1 000名新生的身体素质,将这些学生编号为1,2,…,1 000,从这些新生中用系统抽样方法等距抽取100名学生进行体质测验.若46号学生被抽到,则下面4名学生中被抽到的是( )
A.8号学生 B.200号学生
C.616号学生 D.815号学生
C
A
7.(2021·全国甲卷)为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
C
解析:由频率分布直方图可得,该地农户家庭年收入低于4.5万元和不低于10.5万元的频率分别为0.06和0.10,则农户比率分别为6%和10%,故A、B中结论正确;家庭年收入介于4.5万元和8.5万元之间的频率为0.10+0.14+0.20+0.20=0.64,故D中结论正确;
家庭年收入的平均值为0.02×3+0.04×4+0.10×5+0.14×6+0.20×7+0.20×8+0.10×9+0.10×10+0.04×11+0.02×12+0.02×13+0.02×14=7.68万元,因为7.68>6.5,所以估计该地区农户家庭年收入的平均值超过6.5万元,故C中结论不正确.
8.(2021·新高考全国Ⅰ卷)有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回地随机取两次,每次取1个球.甲表示事件“第一次取出的球的数字是1”,乙表示事件“第二次取出的球的数字是2”,丙表示事件“两次取出的球的数字之和是8”,丁表示事件“两次取出的球的数字之和是7”,则( )
A.甲与丙相互独立 B.甲与丁相互独立
C.乙与丙相互独立 D.丙与丁相互独立
B
9.(2019·全国卷Ⅰ)甲、乙两队进行篮球决赛,采取七场四胜制(当一队赢得四场胜利时,该队获胜,决赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主主客客主客主”.设甲队主场取胜的概率为0.6,客场取胜的概率为0.5,且各场比赛结果相互独立,则甲队以4∶1获胜的概率是________.
解析:甲队以4∶1获胜,甲队在第5场(主场)获胜,前4场中有一场输.
若在主场输一场,则概率为2×0.6×0.4×0.5×0.5×0.6;
若在客场输一场,则概率为2×0.6×0.6×0.5×0.5×0.6.
∴甲队以4∶1获胜的概率P=2×0.6×0.5×0.5×(0.6+0.4)×0.6=0.18.
答案:0.18
[把脉考情]
考什么 1.抽样方法(系统抽样、分层抽样)的应用.
2.古典概型与几何概型求法.
3.用样本估计总体的应用.
4.相互独立事件的概率,独立重复试验的应用.
新动向 1.在选择和填空题中继续考查抽样方法、用样本估计总体及概率的求法.
2.与概率交汇考查概率与统计的综合应用.
解析:由题意得,抽取的样本容量为(15 500+7 500+5 000)×4%=1 120,抽取的高中生参与家务劳动的人数为5 000×0.55×4%=110.
答案:C
C
3.(2021·重庆模拟)为了更好地支持中小型企业的发展,某市决定对部分企业的税收进行适当的减免,某机构调查了当地的中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,下面三个结论:
①样本数据落在区间[300,500)的频率为0.45;
②如果规定年收入在500万元以内的企业才能享受减免税收政策,估计有55%的当地中小型企业能享受到减免税收政策;
③样本的中位数为480万元.
其中正确结论的个数为( )
A.0 B.1
C.2 D.3
D
4.将甲、乙两个篮球队10场比赛的得分数据整理成如图所示的茎叶图,由图可知( )
A.甲队得分的众数是3
B.甲、乙两队得分在[30,39)分数段频率相等
C.甲、乙两队得分的极差相等
D.乙队得分的中位数是38.5
D
1.众数、中位数、平均数与直方图的关系
(1)众数为频率分布直方图中最高矩形的底边中点的横坐标.
(2)中位数为平分频率分布直方图面积且垂直于横轴的直线与横轴交点的横坐标.
(3)平均数等于频率分布直方图中每个小矩形的面积乘小矩形底边中点的横坐标之和.
2.方差的计算与含义
计算方差首先要计算平均数,再按照方差的计算公式进行计算,方差和标准差是描述一个样本和总体的波动大小的特征数,方差、标准差越大说明波动越大.
D
(2)(2021·黑龙江模拟)千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了所在地区A的100天日落情况和夜晚天气,得到如下2×2列联表,并计算得到K2≈19.05.下列小波对地区A的天气判断不正确的是( )
B
P(K2≥k) 0.050 0.010 0.001
k 3.841 6.635 10.828
,
A
C
A
A
B
1.古典概型概率的求解关键及注意点
(1)正确求出基本事件总数和所求概率事件包含的基本事件总数.
(2)对于较复杂的题目条件计数时要正确分类,分类时应不重不漏.
2.几何概型的适用条件及求解关键
(1)当构成试验的结果的区域为长度、面积、体积、弧长、夹角等时,应考虑使用几何概型求解.
(2)求解关键是寻找构成试验的全部结果的区域和事件发生的区域,有时需要设出变量,在坐标系中表示所需要的区域.
B
B
2.复杂事件概率的求法
(1)直接法:正确分析复杂事件的构成,求复杂事件转化为几个彼此互斥的事件的和事件或几个相互独立事件同时发生的积事件或一独立重复试验问题,然后用相应概率公式求解.
(2)间接法:当复杂事件正面情况比较多,反面情况较少时,则可利用其对立事件进行求解.对于“至少”“至多”等问题往往也用这种方法求解.
C
C
https://www.21cnjy.com/help/help_extract.php
同课章节目录
