20专题提能 破解解析几何中重、难点策略——2022高考数学二轮复习课件
文档属性
| 名称 | 20专题提能 破解解析几何中重、难点策略——2022高考数学二轮复习课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 16:02:19 | ||
图片预览



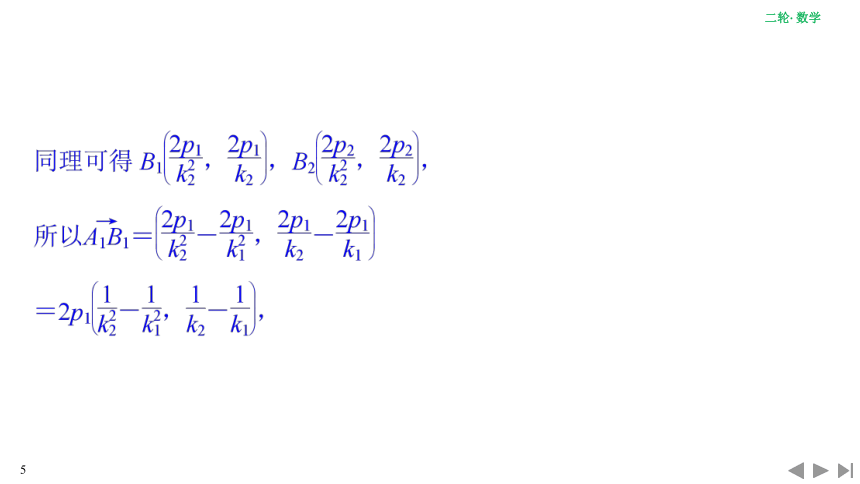
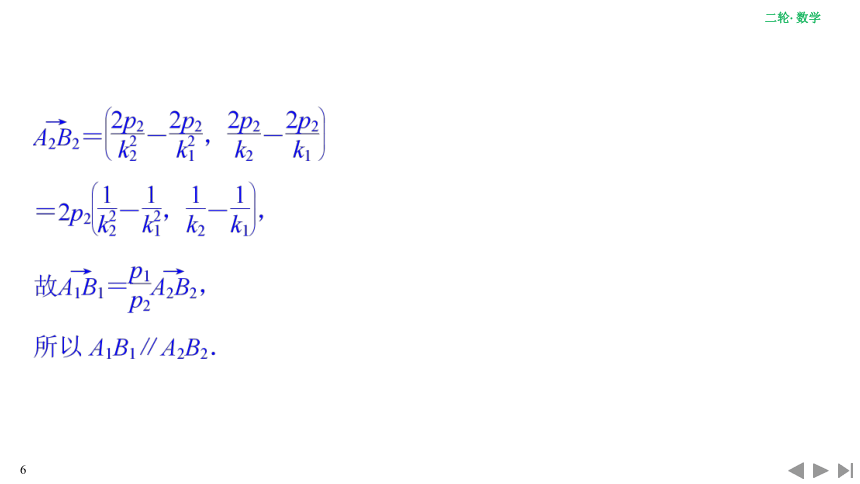





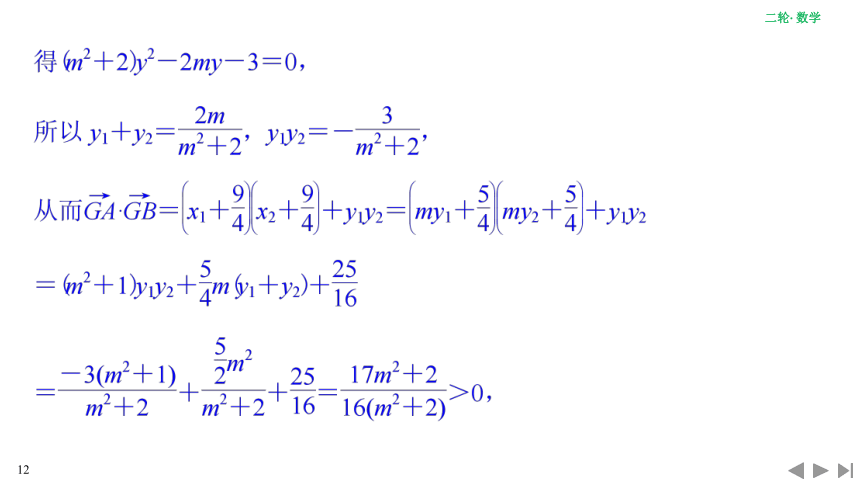
文档简介
(共55张PPT)
20专项提升 破解解析几何中重、难点策略
二轮复习
(一)用向量破解圆锥曲线中的夹角与共线问题
1.利用向量解决两直线的平行或点共线问题
证明两直线平行有两种方法:一是利用a与b共线的充要条件:当且仅当存在实数λ,使a=λb成立;二是利用向量的坐标形式,即利用两个向量a=(x1,y1),b=(x2,y2)共线的充要条件x1y2-x2y1=0解答,其中,a,b为两直线的方向向量.证明三点共线可转化为两个向量共线来证明.
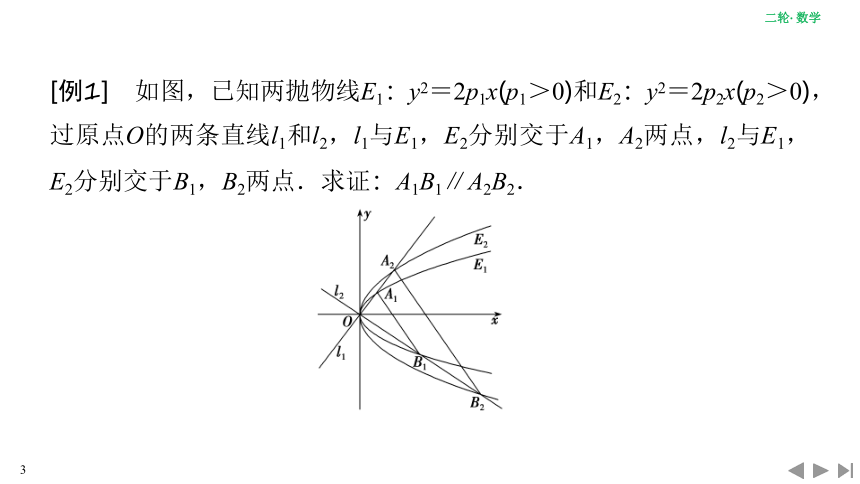
[例1] 如图,已知两抛物线E1:y2=2p1x(p1>0)和E2:y2=2p2x(p2>0),过原点O的两条直线l1和l2,l1与E1,E2分别交于A1,A2两点,l2与E1,E2分别交于B1,B2两点.求证:A1B1∥A2B2.
本题也可以利用两直线的斜率相等来证明A1B1∥A2B2,但计算量较大,而利用向量法解题将大大减少计算量.
2.利用向量解决与角度有关的问题
利用向量的数量积的符号,可以判断这两个向量的夹角是锐角、直角还是钝角,进而可以判断三角形的形状和点与圆的位置关系.
本题也可以通过利用根与系数的关系确定圆心,然后计算圆心到点G的距离并和半径比较得解,由于要用到两点间的距离公式,出现根式,解题过程将十分复杂;但利用向量,通过判断数量积的正负来确定点和圆的位置关系,就不会出现根式,计算量大大减少.本题综合性较强,较好地考查了学生分析问题、解决问题的能力.
(二)减少解析几何运算量的4个策略
中学解析几何是将几何图形置于直角坐标系中,用方程的观点来研究曲线,体现了用代数的方法解决几何问题的优越性,但有时运算量过大,或需繁杂的讨论,这些都会影响解题的速度,甚至会中止解题的过程,达到“望题兴叹”的地步,特别是高考过程中,在规定的时间内,保质保量完成解题的任务,计算能力是一个重要的方向.为此,从以下几个方面探索减轻运算量的方法和技巧,合理简化解题过程,优化思维过程.
1.巧用定义,优化过程
定义是导出其性质的“发源地”,解题时,应善于运用圆锥曲线的定义,以数形结合思想为指导,把定量运算与定性分析有机结合起来,则可使解题计算量简化,使解题构筑在较高的水平上.
D
本题巧妙运用椭圆和双曲线的定义建立|AF1|,|AF2|的等量关系,从而快速求出双曲线实半轴长a的值,进而求出双曲线的离心率,大大降低了运算量.
2.巧用根与系数的关系,化繁为简
某些涉及线段长度关系的问题可以通过解方程、求坐标,用距离公式计算长度的方法来解;但也可以利用一元二次方程,使相关的点的同名坐标为方程的根,由根与系数的关系求出两根间的关系或有关线段长度间的关系.后者往往计算量小,解题过程简捷.
3.借助曲线系理清规律
利用曲线系解题,往往简捷明快,事半功倍,所以灵活运用曲线系是解析几何中重要的解题方法和技巧之一.
B
本题利用了共渐近线系双曲线方程,可使问题马上得到解决.避免了复杂的判断、可能的分类讨论、繁杂的解方程组,事半功倍.
A
4.巧引参数,化难为易
换元引参是一种重要的数学方法,特别是解析几何中的最值问题、不等式问题等,利用换元引参使一些关系能够相互联系起来,激活了解题的方法,往往能化难为易,事半功倍.
常见的参数可以选择点的坐标、直线的斜率、直线的倾斜角等.在换元过程中,还要注意代换的等价性,防止扩大或缩小原来变量的取值范围或改变原题条件.
求解本题利用椭圆的参数方程,可快速建立各点之间的联系,降低运算量.
https://www.21cnjy.com/help/help_extract.php
20专项提升 破解解析几何中重、难点策略
二轮复习
(一)用向量破解圆锥曲线中的夹角与共线问题
1.利用向量解决两直线的平行或点共线问题
证明两直线平行有两种方法:一是利用a与b共线的充要条件:当且仅当存在实数λ,使a=λb成立;二是利用向量的坐标形式,即利用两个向量a=(x1,y1),b=(x2,y2)共线的充要条件x1y2-x2y1=0解答,其中,a,b为两直线的方向向量.证明三点共线可转化为两个向量共线来证明.
[例1] 如图,已知两抛物线E1:y2=2p1x(p1>0)和E2:y2=2p2x(p2>0),过原点O的两条直线l1和l2,l1与E1,E2分别交于A1,A2两点,l2与E1,E2分别交于B1,B2两点.求证:A1B1∥A2B2.
本题也可以利用两直线的斜率相等来证明A1B1∥A2B2,但计算量较大,而利用向量法解题将大大减少计算量.
2.利用向量解决与角度有关的问题
利用向量的数量积的符号,可以判断这两个向量的夹角是锐角、直角还是钝角,进而可以判断三角形的形状和点与圆的位置关系.
本题也可以通过利用根与系数的关系确定圆心,然后计算圆心到点G的距离并和半径比较得解,由于要用到两点间的距离公式,出现根式,解题过程将十分复杂;但利用向量,通过判断数量积的正负来确定点和圆的位置关系,就不会出现根式,计算量大大减少.本题综合性较强,较好地考查了学生分析问题、解决问题的能力.
(二)减少解析几何运算量的4个策略
中学解析几何是将几何图形置于直角坐标系中,用方程的观点来研究曲线,体现了用代数的方法解决几何问题的优越性,但有时运算量过大,或需繁杂的讨论,这些都会影响解题的速度,甚至会中止解题的过程,达到“望题兴叹”的地步,特别是高考过程中,在规定的时间内,保质保量完成解题的任务,计算能力是一个重要的方向.为此,从以下几个方面探索减轻运算量的方法和技巧,合理简化解题过程,优化思维过程.
1.巧用定义,优化过程
定义是导出其性质的“发源地”,解题时,应善于运用圆锥曲线的定义,以数形结合思想为指导,把定量运算与定性分析有机结合起来,则可使解题计算量简化,使解题构筑在较高的水平上.
D
本题巧妙运用椭圆和双曲线的定义建立|AF1|,|AF2|的等量关系,从而快速求出双曲线实半轴长a的值,进而求出双曲线的离心率,大大降低了运算量.
2.巧用根与系数的关系,化繁为简
某些涉及线段长度关系的问题可以通过解方程、求坐标,用距离公式计算长度的方法来解;但也可以利用一元二次方程,使相关的点的同名坐标为方程的根,由根与系数的关系求出两根间的关系或有关线段长度间的关系.后者往往计算量小,解题过程简捷.
3.借助曲线系理清规律
利用曲线系解题,往往简捷明快,事半功倍,所以灵活运用曲线系是解析几何中重要的解题方法和技巧之一.
B
本题利用了共渐近线系双曲线方程,可使问题马上得到解决.避免了复杂的判断、可能的分类讨论、繁杂的解方程组,事半功倍.
A
4.巧引参数,化难为易
换元引参是一种重要的数学方法,特别是解析几何中的最值问题、不等式问题等,利用换元引参使一些关系能够相互联系起来,激活了解题的方法,往往能化难为易,事半功倍.
常见的参数可以选择点的坐标、直线的斜率、直线的倾斜角等.在换元过程中,还要注意代换的等价性,防止扩大或缩小原来变量的取值范围或改变原题条件.
求解本题利用椭圆的参数方程,可快速建立各点之间的联系,降低运算量.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
