29专项提升 函数与导数综合问题的突破策略——2022高考数学二轮复习课件
文档属性
| 名称 | 29专项提升 函数与导数综合问题的突破策略——2022高考数学二轮复习课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 16:02:19 | ||
图片预览









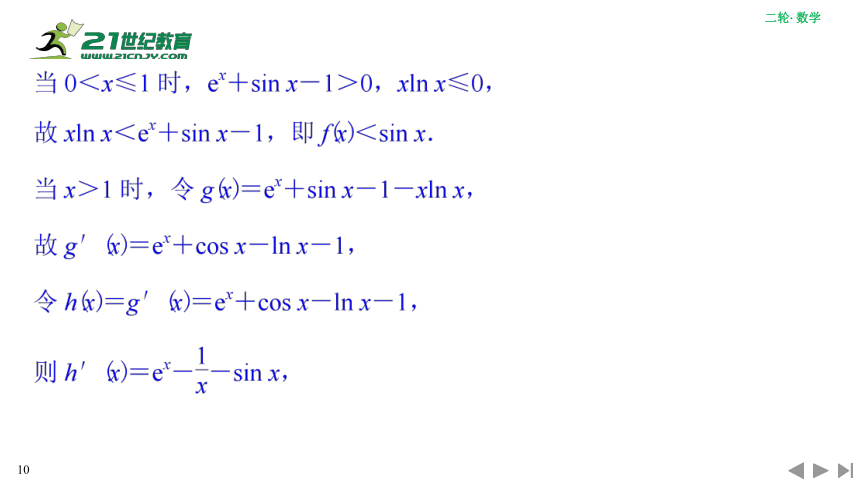


文档简介
(共59张PPT)
29专项提升 函数与导数综合问题的突破策略
二轮复习
本题是应用导数证明不等式.证明的关键在于构造适当的函数,然后在相应区间上用二次求导的办法判定导数的符号,获得函数的单调性,再利用单调性证明不等式.
当导数值等于0这个方程求解困难时,考虑用二次求导不失为一种妙法.
(二)消元消参巧构造、妙解极值点偏移问题
1.极值点偏移的含义、判定
极值点偏移的含义
若单峰函数f(x)的极值点为x0,则极值点的偏移问题的图示及函数值的大小关系如下表所示.
2.函数极值点偏移问题的题型及解法
(1)极值点偏移问题的题设一般有以下四种形式:
①若函数f(x)在定义域上存在两个零点x1,x2(x1≠x2),求证:x1+x2>2x0(x0为函数f(x)的极值点);
②若在函数f(x)的定义域上存在x1,x2(x1≠x2)满足f(x1)=f(x2),求证:x1+x2>2x0(x0为函数f(x)的极值点);
上述解题过程就是解决极值点偏移问题的最基本的方法,共有四个解题要点:
(1)求函数g(x)的极值点x0.
(2)构造函数F(x)=g(x0+x)-g(x0-x).
(3)确定函数F(x)的单调性.
(4)结合F(0)=0,确定g(x0+x)与g(x0-x)的大小关系.
其口诀为:极值偏离对称轴,构造函数觅行踪,四个步骤环相扣,两次单调紧跟随.
该方法的关键是巧妙引入变量s,然后利用等量关系,把t1,t2消掉,从而构造相应的函数,转化所证问题.其解题要点为:
(1)取差构元:记s=t2-t1,则t2=t1+s,利用该式消掉t2.
(2)巧解消参:利用g(t1)=g(t2),构造方程,解之,利用s表示t1.
(3)构造函数:依据消参之后所得不等式的形式,构造关于s的函数G(s).
(4)转化求解:利用导数研究函数G(s)的单调性和最小值,从而证得结论.
https://www.21cnjy.com/help/help_extract.php
29专项提升 函数与导数综合问题的突破策略
二轮复习
本题是应用导数证明不等式.证明的关键在于构造适当的函数,然后在相应区间上用二次求导的办法判定导数的符号,获得函数的单调性,再利用单调性证明不等式.
当导数值等于0这个方程求解困难时,考虑用二次求导不失为一种妙法.
(二)消元消参巧构造、妙解极值点偏移问题
1.极值点偏移的含义、判定
极值点偏移的含义
若单峰函数f(x)的极值点为x0,则极值点的偏移问题的图示及函数值的大小关系如下表所示.
2.函数极值点偏移问题的题型及解法
(1)极值点偏移问题的题设一般有以下四种形式:
①若函数f(x)在定义域上存在两个零点x1,x2(x1≠x2),求证:x1+x2>2x0(x0为函数f(x)的极值点);
②若在函数f(x)的定义域上存在x1,x2(x1≠x2)满足f(x1)=f(x2),求证:x1+x2>2x0(x0为函数f(x)的极值点);
上述解题过程就是解决极值点偏移问题的最基本的方法,共有四个解题要点:
(1)求函数g(x)的极值点x0.
(2)构造函数F(x)=g(x0+x)-g(x0-x).
(3)确定函数F(x)的单调性.
(4)结合F(0)=0,确定g(x0+x)与g(x0-x)的大小关系.
其口诀为:极值偏离对称轴,构造函数觅行踪,四个步骤环相扣,两次单调紧跟随.
该方法的关键是巧妙引入变量s,然后利用等量关系,把t1,t2消掉,从而构造相应的函数,转化所证问题.其解题要点为:
(1)取差构元:记s=t2-t1,则t2=t1+s,利用该式消掉t2.
(2)巧解消参:利用g(t1)=g(t2),构造方程,解之,利用s表示t1.
(3)构造函数:依据消参之后所得不等式的形式,构造关于s的函数G(s).
(4)转化求解:利用导数研究函数G(s)的单调性和最小值,从而证得结论.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
