35紧扣高考方向 解密命题趋势——2022高考数学二轮复习课件
文档属性
| 名称 | 35紧扣高考方向 解密命题趋势——2022高考数学二轮复习课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 16:02:44 | ||
图片预览










文档简介
(共42张PPT)
35紧扣高考方向
解锁命题趋势
二轮复习
2017版(2020修订)数学课程标准中强调高考命题要严格落实《国务院关于深化考试招生制度改革的实施意见》中提出的深化高考考试内容改革,依据高校人才选拔要求和国家课程标准,科学设计命题内容,增强基础性、综合性,着重考查学生独立思考和运用所学知识分析问题、解决问题的能力.高考考试内容改革全面贯彻党的教育方针,
落实构建德智体美劳全面培养教育体系的要求,以立德树人为鲜明导向,以促进素质教育发展为基本遵循,科学构建基于德智体美劳全面发展要求的高考评价体系.高考评价体系由“一核四层四翼”组成,包括考查目的、考查内容和考查要求.
具体说来命题变化主要有以下三个方面的新趋势.
命题趋势一 与“五育”结合培养时代新人
1.德育为先,立德树人
[例1] 中国女排的影响力早已超越体育本身的意义,不仅是时代的集体记忆,更是激励国人继续奋斗、自强不息的精神符号.某大学组织学生看过电影《夺冠》后,举行了“学习女排精神,塑造健康体魄”
的主题活动,一段时间后,学生的身体素质明显提高.现随机抽取800个学生进行体能测试,成绩的频率分布直方图如图所示,数据(单位:分)分成[40,50),[50,60),…,[90,100]六组,则成绩落在[70,80)内的人数为( )
A.12 B.120
C.24 D.240
[解析] 易知题图中所有小长方形(包括区间[70,80)对应的小长方形)的面积之和等于1,则成绩落在[70,80)内的频率为p=1-10×(0.01+0.015+0.015+0.025+0.005)=0.3.因为一共抽取800个学生进行体能测试,所以样本容量为800,所以成绩落在[70,80)内的人数为800×0.3=240.
[答案] D
[点评] 本题以电影《夺冠》为背景考查用样本估计总体,体现了德育的素养导向.
A
[点评] 本题以“唐代诗人李颀的诗《古从军行》中的数学问题”为背景,考查直线与圆的位置关系、对称性问题与最值问题,体现了智育的素养导向.破解此类最值问题的关键在于“化折为直”,即把一动点到两定点的距离和的最小值问题,通过对称思想,转化为两点间的距离问题.
3.体育为基,强健体魄
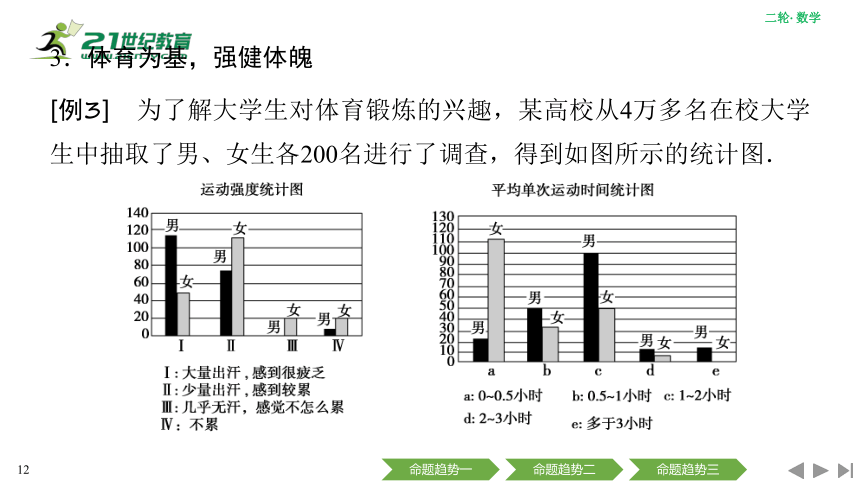
[例3] 为了解大学生对体育锻炼的兴趣,某高校从4万多名在校大学生中抽取了男、女生各200名进行了调查,得到如图所示的统计图.
对比图中信息并进行分析,下列说法正确的是( )
A.大量出汗并感到很疲乏的男生人数是女生人数的2倍
B.男生中运动时间超过1小时的超过70%
C.女生的平均运动强度高于男生的平均运动强度
D.运动时间在0.5~1小时内的男生人数与运动时间在1~2小时内的女生人数相同
D
[点评] 本题以“大学生运动强度和单次运动时间”为背景,借助条形图考查了统计知识.
B
[点评] 本题以“正八边形形状的U盘”“正八边形窗户”为背景,结合平面向量考查了向量夹角知识体会对称之美,体现了美育导向.
5.劳育为本,习行技法
[例5] (2021·榆林模拟)数学实践活动小组到附近的湿地公园测量园内雕塑的高度.如图,用测角仪在A处测得雕塑顶点C的仰角为30°,再往雕塑方向前进4 m 至B处,测得仰角为45°,则该雕塑高度为________.(测角仪高度忽略不计,结果不取近似值)
[点评] 本题以“学生到湿地公园测量园内雕塑的高度”为背景,考查解直角三角形、正弦定理等知识,引导学生积极关注并参与社会活动.
命题趋势二 与社会热点、生产生活结合,尽显责任担当
[例6] (交通出行)2021年春节期间,我国高速公路
小型客车可免费通行.某路桥公司为了解春节期间
车辆出行的高峰情况,在某高速公路收费点记录了
大年初三上午9:20~10:40这一时间段内通过的车辆数,统计发现这一时间段内共有600辆车通过该收费点,它们通过该收费点的时刻的频率分布直方图如图所示,其中时间段9:20~9:40记作区间[20,40),9:40~10:00记作[40,60),10:00~10:20记作[60,80),10:20~10:40记作[80,100].例如:10点04分记作时刻64.
(1)估计这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值(同一组中的数据用该组区间的中点值为代表);
(2)为了对数据进行分析,现采用分层抽样的方法从这600辆车中抽取10辆,再从这10辆车中随机抽取4辆,设抽到的4辆车中,在9:20~10:00之间通过的车辆数为X,求X的分布列与数学期望;
(3)由大数据分析可知,车辆每天通过该收费点的时刻服从正态分布N(μ,σ2),其中μ可用这600辆车在9:20~10:40这一时间段内通过该收费点的时刻的平均值近似代替,σ2可用样本的方差近似代替(同一组中的数据用该组区间的中点值为代表).已知大年初五全天共有1 000辆车通过该收费点,估计在9:46~10:22这一时间段内通过的车辆数(结果保留整数).
参考数据:若T~N(μ,σ2),则①P(μ-σ<T≤μ+σ)≈0.682 6;②P(μ-2σ<T≤μ+2σ)≈0.954 4;③P(μ-3σ<T≤μ+3σ)≈0.997 4.
[解析] (1)这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值为(30×0.005+50×0.015+70×0.020+90×0.010)×20=64,即10点04分.
(3)由(1)可得μ=64,
σ2=(30-64)2×0.1+(50-64)2×0.3+(70-64)2×0.4+(90-64)2×0.2=324,所以σ=18.
9:46与10:22对应的时刻分别为46,82,即64-18,64+18,
由T~N(μ,σ2),得P(64-18<T≤64+18)≈0.682 6,
所以估计在9:46~10:22这一时间段内通过的车辆数为
1 000×0.682 6≈683.
[点评] 本题以国家节假日高速公路小型客车免费出行为背景,考查了正态分布、频率分布直方图、分层抽样等相关知识,体现了以社会热点为命题新情境这一素养要求.
D
[点评] 本题以“北斗三号全球卫星导航系统”为背景考查三角函数的定义、质点的轨迹等知识,意在考查数学建模、逻辑推理和数学运算核心素养.求解此类题的关键是能从长串的文字语言中提炼出关键字眼,并能根据关键字眼寻找轨迹方程,即可判断函数模型.
[例8] (5G技术)5G智能手机是全世界很多年轻人非常喜欢的产品.为了研究某城市甲、乙两个5G智能手机专卖店的销售状况,统计了2020年4月到9月甲、乙两店每月的营业额(单位:万元),得到如图所示的折线图,则下列说法不正确的是( )
A.根据甲店的月营业额折线图可知,该店月营业额的平均值在[31,32]内
B.根据乙店的月营业额折线图可知,该店月营业额总体呈上升趋势
C.根据甲、乙两店的月营业额折线图可知,乙店的月营业额极差比甲店小
D.根据甲、乙两店的月营业额折线图可知,7,8,9月份的总营业额甲店比乙店少
[答案] C
[点评] 本题以5G技术为背景,考查了图象信息处理问题,处理此类题的关键是正确读懂读准图中数据信息.
https://www.21cnjy.com/help/help_extract.php
35紧扣高考方向
解锁命题趋势
二轮复习
2017版(2020修订)数学课程标准中强调高考命题要严格落实《国务院关于深化考试招生制度改革的实施意见》中提出的深化高考考试内容改革,依据高校人才选拔要求和国家课程标准,科学设计命题内容,增强基础性、综合性,着重考查学生独立思考和运用所学知识分析问题、解决问题的能力.高考考试内容改革全面贯彻党的教育方针,
落实构建德智体美劳全面培养教育体系的要求,以立德树人为鲜明导向,以促进素质教育发展为基本遵循,科学构建基于德智体美劳全面发展要求的高考评价体系.高考评价体系由“一核四层四翼”组成,包括考查目的、考查内容和考查要求.
具体说来命题变化主要有以下三个方面的新趋势.
命题趋势一 与“五育”结合培养时代新人
1.德育为先,立德树人
[例1] 中国女排的影响力早已超越体育本身的意义,不仅是时代的集体记忆,更是激励国人继续奋斗、自强不息的精神符号.某大学组织学生看过电影《夺冠》后,举行了“学习女排精神,塑造健康体魄”
的主题活动,一段时间后,学生的身体素质明显提高.现随机抽取800个学生进行体能测试,成绩的频率分布直方图如图所示,数据(单位:分)分成[40,50),[50,60),…,[90,100]六组,则成绩落在[70,80)内的人数为( )
A.12 B.120
C.24 D.240
[解析] 易知题图中所有小长方形(包括区间[70,80)对应的小长方形)的面积之和等于1,则成绩落在[70,80)内的频率为p=1-10×(0.01+0.015+0.015+0.025+0.005)=0.3.因为一共抽取800个学生进行体能测试,所以样本容量为800,所以成绩落在[70,80)内的人数为800×0.3=240.
[答案] D
[点评] 本题以电影《夺冠》为背景考查用样本估计总体,体现了德育的素养导向.
A
[点评] 本题以“唐代诗人李颀的诗《古从军行》中的数学问题”为背景,考查直线与圆的位置关系、对称性问题与最值问题,体现了智育的素养导向.破解此类最值问题的关键在于“化折为直”,即把一动点到两定点的距离和的最小值问题,通过对称思想,转化为两点间的距离问题.
3.体育为基,强健体魄
[例3] 为了解大学生对体育锻炼的兴趣,某高校从4万多名在校大学生中抽取了男、女生各200名进行了调查,得到如图所示的统计图.
对比图中信息并进行分析,下列说法正确的是( )
A.大量出汗并感到很疲乏的男生人数是女生人数的2倍
B.男生中运动时间超过1小时的超过70%
C.女生的平均运动强度高于男生的平均运动强度
D.运动时间在0.5~1小时内的男生人数与运动时间在1~2小时内的女生人数相同
D
[点评] 本题以“大学生运动强度和单次运动时间”为背景,借助条形图考查了统计知识.
B
[点评] 本题以“正八边形形状的U盘”“正八边形窗户”为背景,结合平面向量考查了向量夹角知识体会对称之美,体现了美育导向.
5.劳育为本,习行技法
[例5] (2021·榆林模拟)数学实践活动小组到附近的湿地公园测量园内雕塑的高度.如图,用测角仪在A处测得雕塑顶点C的仰角为30°,再往雕塑方向前进4 m 至B处,测得仰角为45°,则该雕塑高度为________.(测角仪高度忽略不计,结果不取近似值)
[点评] 本题以“学生到湿地公园测量园内雕塑的高度”为背景,考查解直角三角形、正弦定理等知识,引导学生积极关注并参与社会活动.
命题趋势二 与社会热点、生产生活结合,尽显责任担当
[例6] (交通出行)2021年春节期间,我国高速公路
小型客车可免费通行.某路桥公司为了解春节期间
车辆出行的高峰情况,在某高速公路收费点记录了
大年初三上午9:20~10:40这一时间段内通过的车辆数,统计发现这一时间段内共有600辆车通过该收费点,它们通过该收费点的时刻的频率分布直方图如图所示,其中时间段9:20~9:40记作区间[20,40),9:40~10:00记作[40,60),10:00~10:20记作[60,80),10:20~10:40记作[80,100].例如:10点04分记作时刻64.
(1)估计这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值(同一组中的数据用该组区间的中点值为代表);
(2)为了对数据进行分析,现采用分层抽样的方法从这600辆车中抽取10辆,再从这10辆车中随机抽取4辆,设抽到的4辆车中,在9:20~10:00之间通过的车辆数为X,求X的分布列与数学期望;
(3)由大数据分析可知,车辆每天通过该收费点的时刻服从正态分布N(μ,σ2),其中μ可用这600辆车在9:20~10:40这一时间段内通过该收费点的时刻的平均值近似代替,σ2可用样本的方差近似代替(同一组中的数据用该组区间的中点值为代表).已知大年初五全天共有1 000辆车通过该收费点,估计在9:46~10:22这一时间段内通过的车辆数(结果保留整数).
参考数据:若T~N(μ,σ2),则①P(μ-σ<T≤μ+σ)≈0.682 6;②P(μ-2σ<T≤μ+2σ)≈0.954 4;③P(μ-3σ<T≤μ+3σ)≈0.997 4.
[解析] (1)这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值为(30×0.005+50×0.015+70×0.020+90×0.010)×20=64,即10点04分.
(3)由(1)可得μ=64,
σ2=(30-64)2×0.1+(50-64)2×0.3+(70-64)2×0.4+(90-64)2×0.2=324,所以σ=18.
9:46与10:22对应的时刻分别为46,82,即64-18,64+18,
由T~N(μ,σ2),得P(64-18<T≤64+18)≈0.682 6,
所以估计在9:46~10:22这一时间段内通过的车辆数为
1 000×0.682 6≈683.
[点评] 本题以国家节假日高速公路小型客车免费出行为背景,考查了正态分布、频率分布直方图、分层抽样等相关知识,体现了以社会热点为命题新情境这一素养要求.
D
[点评] 本题以“北斗三号全球卫星导航系统”为背景考查三角函数的定义、质点的轨迹等知识,意在考查数学建模、逻辑推理和数学运算核心素养.求解此类题的关键是能从长串的文字语言中提炼出关键字眼,并能根据关键字眼寻找轨迹方程,即可判断函数模型.
[例8] (5G技术)5G智能手机是全世界很多年轻人非常喜欢的产品.为了研究某城市甲、乙两个5G智能手机专卖店的销售状况,统计了2020年4月到9月甲、乙两店每月的营业额(单位:万元),得到如图所示的折线图,则下列说法不正确的是( )
A.根据甲店的月营业额折线图可知,该店月营业额的平均值在[31,32]内
B.根据乙店的月营业额折线图可知,该店月营业额总体呈上升趋势
C.根据甲、乙两店的月营业额折线图可知,乙店的月营业额极差比甲店小
D.根据甲、乙两店的月营业额折线图可知,7,8,9月份的总营业额甲店比乙店少
[答案] C
[点评] 本题以5G技术为背景,考查了图象信息处理问题,处理此类题的关键是正确读懂读准图中数据信息.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
