08空间几何体的三视图、表面积与体积及空间线面位置关系的判定——2022高考数学二轮复习课件
文档属性
| 名称 | 08空间几何体的三视图、表面积与体积及空间线面位置关系的判定——2022高考数学二轮复习课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 10.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 16:01:15 | ||
图片预览







文档简介
(共72张PPT)
08空间几何体的三识图、表面积与体积及空间线面位置关系的判定
二轮复习
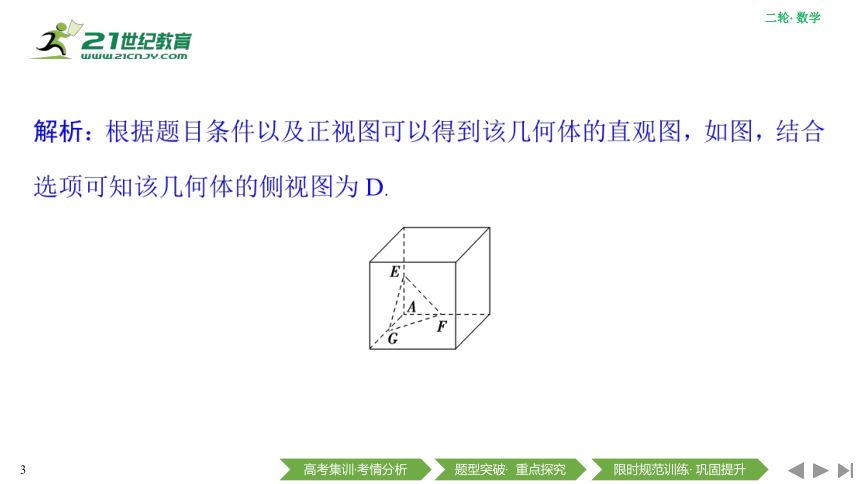
D
D
A
C
A
A
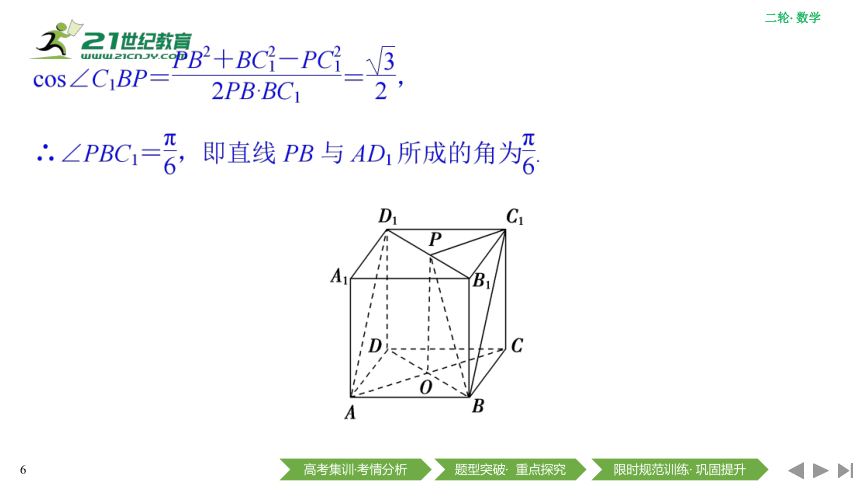
7.(2019·全国卷Ⅲ)如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则( )
A.BM=EN,且直线BM,EN是相交直线
B.BM≠EN,且直线BM,EN是相交直线
C.BM=EN,且直线BM,EN是异面直线
D.BM≠EN,且直线BM,EN是异面直线
B
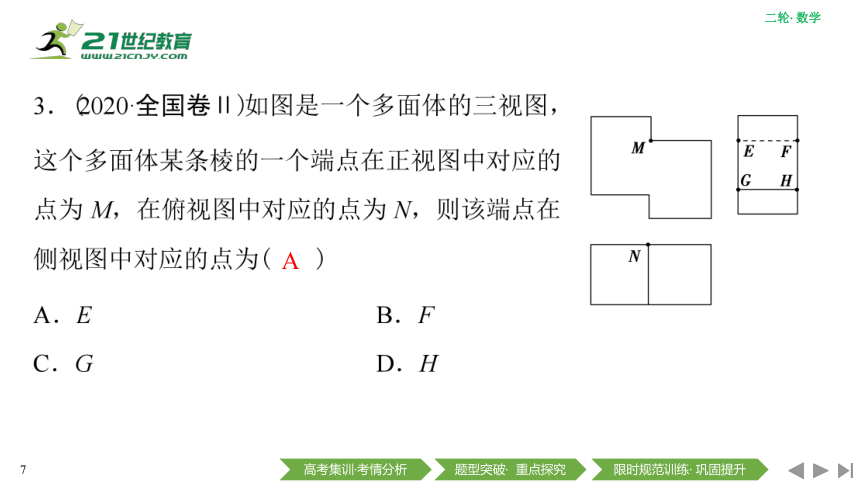
解析:根据“长对正、高平齐、宽相等”及图中数据,可知图②③只能是侧视图,图④⑤只能是俯视图,则组成某个三棱锥的三视图,所选侧视图和俯视图的编号依次是③④或②⑤.若是③④,则原几何体如图1所示;若是②⑤,则原几何体如图2所示.
答案:③④(答案不唯一,②⑤也可以)
[把脉考情]
考什么 1.三视图的判断与几何体的还原.
2.空间几何体的面积与体积的求法.
3.与球有关的切、接问题.
4.空间点、线、面位置关系的判断及应用.
新动向 1.继续在选择、填空题中考查空间几何体的面积与体积的求法,注意数学文化的渗透考查.
2.与空间几何体表面积、体积有关的最值问题是命题的热点,多涉及用基本不等式与导数法求最值.
A
解析:根据几何体的三视图可知该几何体为柱体.当选A时,正视图的中间的竖线应为虚线.选项B,C,D都有可能.
B
D
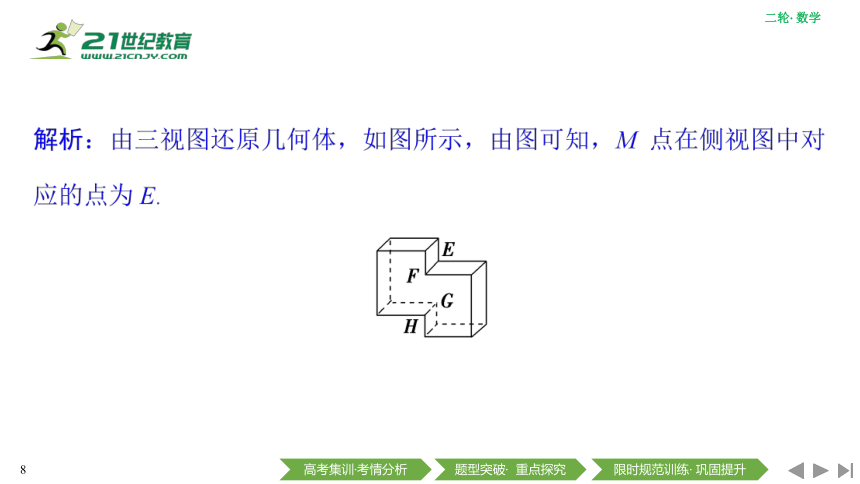
熟练掌握规则几何体的三视图是由三视图还原几何体的基础,在明确三视图画法规则的基础上,按以下步骤可轻松解决此类问题:
C
C
C
求几何体的表面积或体积的策略
(1)对于规则几何体,可直接利用公式计算.
(2)对于不规则几何体,可采用割补法求解;对于某些三棱锥,有时可采用等体积转换法求解.
(3)求解旋转体的表面积和体积时,注意圆柱的轴截面是矩形,圆锥的轴截面是等腰三角形,圆台的轴截面是等腰梯形的应用.
A
C
3.阿基米德(Archimedes,公元前287年—公元前212年)是古希腊伟大的数学家、物理学家和天文学家.他推导出的结论“圆柱内切球体的体积是圆柱体积的三分之二,并且球的表面积也是圆柱表面积的三分之二”是其毕生最满意的数学发现,后人按照他生前的要求,在他的墓碑上刻着一个圆柱容器里放了一个球,如图,该球顶天立地,四周碰边,圆柱的底面直径与高都等于球的直径.若球的体积为36π,则圆柱的表面积为( )
A.36π B.45π
C.54π D.63π
D
1.空间几何体的面积与体积的创新考法
(1)与数学文化交汇考查面积与体积的计算.
(2)与最值交汇创新考查.
2.求解立体几何最值问题的策略
(1)结合图形分析,确定取得最值的临界位置直接求解.
(2)建立目标函数求解与体积、面积有关的最值问题,最值的求法多用基本不等式或导数法.
C
[解析] (1)根据几何体的三视图可知该几何体为底面为等腰直角三角形,高为2的三棱锥.如图所示:
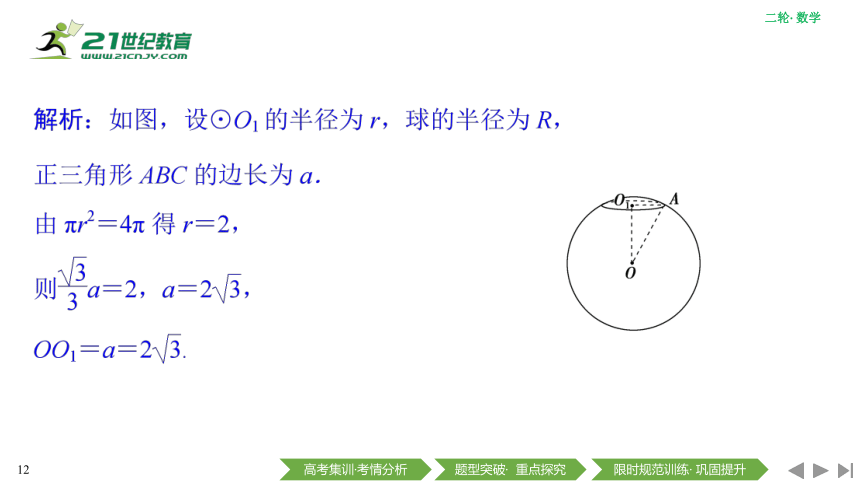
与球有关的“切”“接”问题的处理方法
(1)“切”的处理:解决与球有关的内切问题主要是指球内切多面体与旋转体,解答时要先找准切点,通过作截面来解决.如果内切的是多面体,则多通过多面体过球心的对角面来作截面.
(2)“接”的处理:把一个多面体的几个顶点放在球面上即球的外接问题.解决这类问题的关键是抓住外接的特点,即球心到多面体的顶点的距离等于球的半径.
C
B
B
/
D
3.如图,在三棱锥P-ABC中,已知PA⊥底面ABC,AB⊥BC,E,F分别是线段PB,PC上的动点,则下列说法错误的是( )
A.当AE⊥PB时,△AEF一定是直角三角形
B.当AF⊥PC对,△AEF一定是直角三角形
C.当EF∥平面ABC时,△AEF一定是直角三角形
D.当PC⊥平面AEF时,△AEF一定是直角三角形
B
解析:由PA⊥底面ABC,得PA⊥BC.又AB⊥BC,PA∩AB=A,所以BC⊥平面PAB,BC⊥AE.又AE⊥PB,BC∩PB=B,所以AE⊥平面PBC,所以AE⊥EF,故A正确;当EF∥平面ABC时,因为EF 平面PBC,平面PBC∩平面ABC=BC,所以EF∥BC,故EF⊥平面PAB,AE⊥EF,故C正确;当PC⊥平面AEF时,PC⊥AE.又BC⊥AE,PC∩BC=C,所以AE⊥平面PBC,所以AE⊥EF,故D正确.
判断与空间位置关系有关命题真假的方法
(1)借助空间线面平行、面面平行、线面垂直、面面垂直的判定定理和性质定理进行判断.
(2)借助空间几何模型,如从长方体模型、四面体模型等模型中观察线面位置关系,结合有关定理,进行肯定或否定.
(3)借助反证法,当从正面入手较难时,可利用反证法,推出与题设或公认的结论相矛盾的命题,进而作出判断.
https://www.21cnjy.com/help/help_extract.php
08空间几何体的三识图、表面积与体积及空间线面位置关系的判定
二轮复习
D
D
A
C
A
A
7.(2019·全国卷Ⅲ)如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则( )
A.BM=EN,且直线BM,EN是相交直线
B.BM≠EN,且直线BM,EN是相交直线
C.BM=EN,且直线BM,EN是异面直线
D.BM≠EN,且直线BM,EN是异面直线
B
解析:根据“长对正、高平齐、宽相等”及图中数据,可知图②③只能是侧视图,图④⑤只能是俯视图,则组成某个三棱锥的三视图,所选侧视图和俯视图的编号依次是③④或②⑤.若是③④,则原几何体如图1所示;若是②⑤,则原几何体如图2所示.
答案:③④(答案不唯一,②⑤也可以)
[把脉考情]
考什么 1.三视图的判断与几何体的还原.
2.空间几何体的面积与体积的求法.
3.与球有关的切、接问题.
4.空间点、线、面位置关系的判断及应用.
新动向 1.继续在选择、填空题中考查空间几何体的面积与体积的求法,注意数学文化的渗透考查.
2.与空间几何体表面积、体积有关的最值问题是命题的热点,多涉及用基本不等式与导数法求最值.
A
解析:根据几何体的三视图可知该几何体为柱体.当选A时,正视图的中间的竖线应为虚线.选项B,C,D都有可能.
B
D
熟练掌握规则几何体的三视图是由三视图还原几何体的基础,在明确三视图画法规则的基础上,按以下步骤可轻松解决此类问题:
C
C
C
求几何体的表面积或体积的策略
(1)对于规则几何体,可直接利用公式计算.
(2)对于不规则几何体,可采用割补法求解;对于某些三棱锥,有时可采用等体积转换法求解.
(3)求解旋转体的表面积和体积时,注意圆柱的轴截面是矩形,圆锥的轴截面是等腰三角形,圆台的轴截面是等腰梯形的应用.
A
C
3.阿基米德(Archimedes,公元前287年—公元前212年)是古希腊伟大的数学家、物理学家和天文学家.他推导出的结论“圆柱内切球体的体积是圆柱体积的三分之二,并且球的表面积也是圆柱表面积的三分之二”是其毕生最满意的数学发现,后人按照他生前的要求,在他的墓碑上刻着一个圆柱容器里放了一个球,如图,该球顶天立地,四周碰边,圆柱的底面直径与高都等于球的直径.若球的体积为36π,则圆柱的表面积为( )
A.36π B.45π
C.54π D.63π
D
1.空间几何体的面积与体积的创新考法
(1)与数学文化交汇考查面积与体积的计算.
(2)与最值交汇创新考查.
2.求解立体几何最值问题的策略
(1)结合图形分析,确定取得最值的临界位置直接求解.
(2)建立目标函数求解与体积、面积有关的最值问题,最值的求法多用基本不等式或导数法.
C
[解析] (1)根据几何体的三视图可知该几何体为底面为等腰直角三角形,高为2的三棱锥.如图所示:
与球有关的“切”“接”问题的处理方法
(1)“切”的处理:解决与球有关的内切问题主要是指球内切多面体与旋转体,解答时要先找准切点,通过作截面来解决.如果内切的是多面体,则多通过多面体过球心的对角面来作截面.
(2)“接”的处理:把一个多面体的几个顶点放在球面上即球的外接问题.解决这类问题的关键是抓住外接的特点,即球心到多面体的顶点的距离等于球的半径.
C
B
B
/
D
3.如图,在三棱锥P-ABC中,已知PA⊥底面ABC,AB⊥BC,E,F分别是线段PB,PC上的动点,则下列说法错误的是( )
A.当AE⊥PB时,△AEF一定是直角三角形
B.当AF⊥PC对,△AEF一定是直角三角形
C.当EF∥平面ABC时,△AEF一定是直角三角形
D.当PC⊥平面AEF时,△AEF一定是直角三角形
B
解析:由PA⊥底面ABC,得PA⊥BC.又AB⊥BC,PA∩AB=A,所以BC⊥平面PAB,BC⊥AE.又AE⊥PB,BC∩PB=B,所以AE⊥平面PBC,所以AE⊥EF,故A正确;当EF∥平面ABC时,因为EF 平面PBC,平面PBC∩平面ABC=BC,所以EF∥BC,故EF⊥平面PAB,AE⊥EF,故C正确;当PC⊥平面AEF时,PC⊥AE.又BC⊥AE,PC∩BC=C,所以AE⊥平面PBC,所以AE⊥EF,故D正确.
判断与空间位置关系有关命题真假的方法
(1)借助空间线面平行、面面平行、线面垂直、面面垂直的判定定理和性质定理进行判断.
(2)借助空间几何模型,如从长方体模型、四面体模型等模型中观察线面位置关系,结合有关定理,进行肯定或否定.
(3)借助反证法,当从正面入手较难时,可利用反证法,推出与题设或公认的结论相矛盾的命题,进而作出判断.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
