10专项提升 立体几何中的高考热点求解策略——2022高考数学二轮复习课件
文档属性
| 名称 | 10专项提升 立体几何中的高考热点求解策略——2022高考数学二轮复习课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 16:01:15 | ||
图片预览


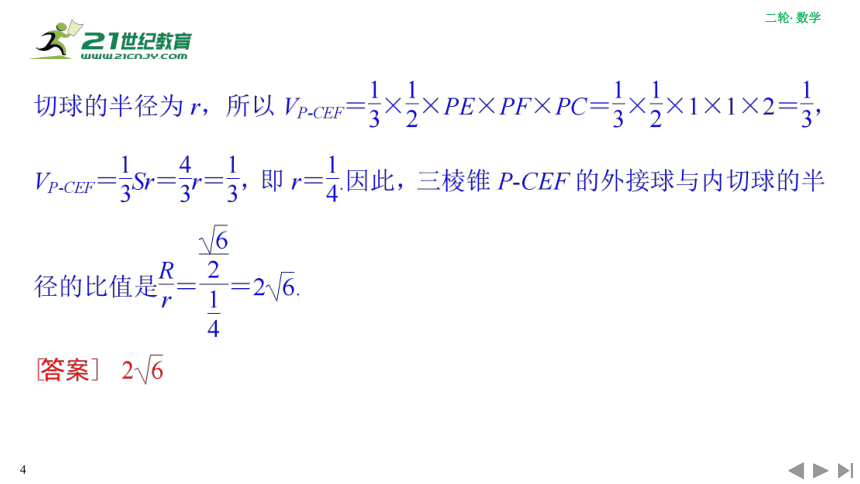






文档简介
(共43张PPT)
10专项提升 立体几何中的高考热点求解策略
二轮复习
(一)构造法解决与球有关的问题
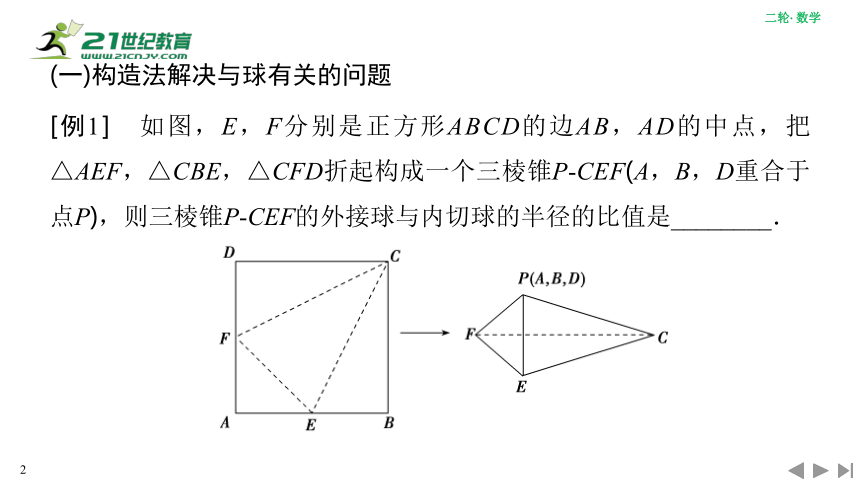
[例1] 如图,E,F分别是正方形ABCD的边AB,AD的中点,把△AEF,△CBE,△CFD折起构成一个三棱锥P CEF(A,B,D重合于点P),则三棱锥P CEF的外接球与内切球的半径的比值是________.
构造长方体或正方体确定球心的途径
(1)正四面体、三条侧棱两两垂直的正三棱锥都分别可构造正方体.
(2)同一个顶点上的三条棱两两垂直的四面体、四个面都是直角三角形的三棱锥、相对的棱相等的三棱锥都分别可构造长方体或正方体.
(3)若已知棱锥中含有线面垂直关系,则可将棱锥构造成长方体或正方体.
(二)割补法解决空间几何体的体积
1.分割法求空间几何体的体积
把一个不规则的几何体分割成几个规则的几何体,求出每个规则几何体的体积,然后进行体积求和即可.
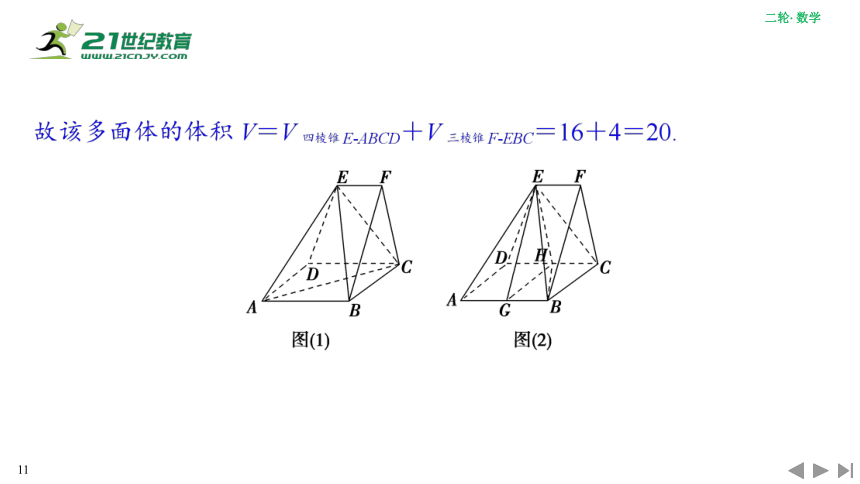
[例2] 如图所示,在多面体ABCDEF中,已知四边形ABCD是边长为4的正方形,EF∥AB,EF=2,EF上任意一点到平面ABCD的距离均为3,求该多面体的体积.
2.补形法求空间几何体的体积
当求某些几何体的体积较困难时,可以将它放置在我们熟悉的几何体中,如正方体、长方体等对称性比较好的几何体,以此来求几何体的体积.
常见情况如下:
①将正四面体补为正方体,如图所示.
②将对棱长相等的三棱锥补成长方体,如图所示.
③将三条侧棱两两垂直的三棱锥补成长方体或正方体,如图所示,PA⊥PB,PA⊥PC,PB⊥PC.
④将三棱锥补成三棱柱或平行六面体,如图(1)(2)所示.
⑤将三棱柱补成平行六面体,如图所示.
⑥将台体补成锥体,如图所示.
[例3] 某几何体的三视图如图所示,
则该几何体的体积为( )
A.12
B.18
C.24
D.30
C
B
(三)翻折与探索性问题
主要考查平面图形与空间图形的转换,且多涉及空间线面、面面的平行与垂直问题的证明或判断,以及探索性问题.
求解平面图形折叠问题的关键和方法
(1)关键:分清翻折前后哪些位置关系和数量关系改变,哪些不变,抓住翻折前后不变的量,充分利用原平面图形的信息是解决问题的突破口.
(2)方法:把平面图形翻折后,经过恰当连线就能得到三棱锥、四棱锥等几何体,从而把问题转化到我们熟悉的几何体中解决.
(1)求证:平面PAE⊥平面ABCE;
(2)若点F在线段PC上,满足PC=4PF,求平面PAE与平面ABF所成的锐二面角的余弦值.
https://www.21cnjy.com/help/help_extract.php
10专项提升 立体几何中的高考热点求解策略
二轮复习
(一)构造法解决与球有关的问题
[例1] 如图,E,F分别是正方形ABCD的边AB,AD的中点,把△AEF,△CBE,△CFD折起构成一个三棱锥P CEF(A,B,D重合于点P),则三棱锥P CEF的外接球与内切球的半径的比值是________.
构造长方体或正方体确定球心的途径
(1)正四面体、三条侧棱两两垂直的正三棱锥都分别可构造正方体.
(2)同一个顶点上的三条棱两两垂直的四面体、四个面都是直角三角形的三棱锥、相对的棱相等的三棱锥都分别可构造长方体或正方体.
(3)若已知棱锥中含有线面垂直关系,则可将棱锥构造成长方体或正方体.
(二)割补法解决空间几何体的体积
1.分割法求空间几何体的体积
把一个不规则的几何体分割成几个规则的几何体,求出每个规则几何体的体积,然后进行体积求和即可.
[例2] 如图所示,在多面体ABCDEF中,已知四边形ABCD是边长为4的正方形,EF∥AB,EF=2,EF上任意一点到平面ABCD的距离均为3,求该多面体的体积.
2.补形法求空间几何体的体积
当求某些几何体的体积较困难时,可以将它放置在我们熟悉的几何体中,如正方体、长方体等对称性比较好的几何体,以此来求几何体的体积.
常见情况如下:
①将正四面体补为正方体,如图所示.
②将对棱长相等的三棱锥补成长方体,如图所示.
③将三条侧棱两两垂直的三棱锥补成长方体或正方体,如图所示,PA⊥PB,PA⊥PC,PB⊥PC.
④将三棱锥补成三棱柱或平行六面体,如图(1)(2)所示.
⑤将三棱柱补成平行六面体,如图所示.
⑥将台体补成锥体,如图所示.
[例3] 某几何体的三视图如图所示,
则该几何体的体积为( )
A.12
B.18
C.24
D.30
C
B
(三)翻折与探索性问题
主要考查平面图形与空间图形的转换,且多涉及空间线面、面面的平行与垂直问题的证明或判断,以及探索性问题.
求解平面图形折叠问题的关键和方法
(1)关键:分清翻折前后哪些位置关系和数量关系改变,哪些不变,抓住翻折前后不变的量,充分利用原平面图形的信息是解决问题的突破口.
(2)方法:把平面图形翻折后,经过恰当连线就能得到三棱锥、四棱锥等几何体,从而把问题转化到我们熟悉的几何体中解决.
(1)求证:平面PAE⊥平面ABCE;
(2)若点F在线段PC上,满足PC=4PF,求平面PAE与平面ABF所成的锐二面角的余弦值.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
