2022年陕西省西安交通大学少年班自主招生数学试题(word含答案)
文档属性
| 名称 | 2022年陕西省西安交通大学少年班自主招生数学试题(word含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 434.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 14:57:49 | ||
图片预览

文档简介
2022年西安交通大学少年班数学试题
1.已知,则的值为______.
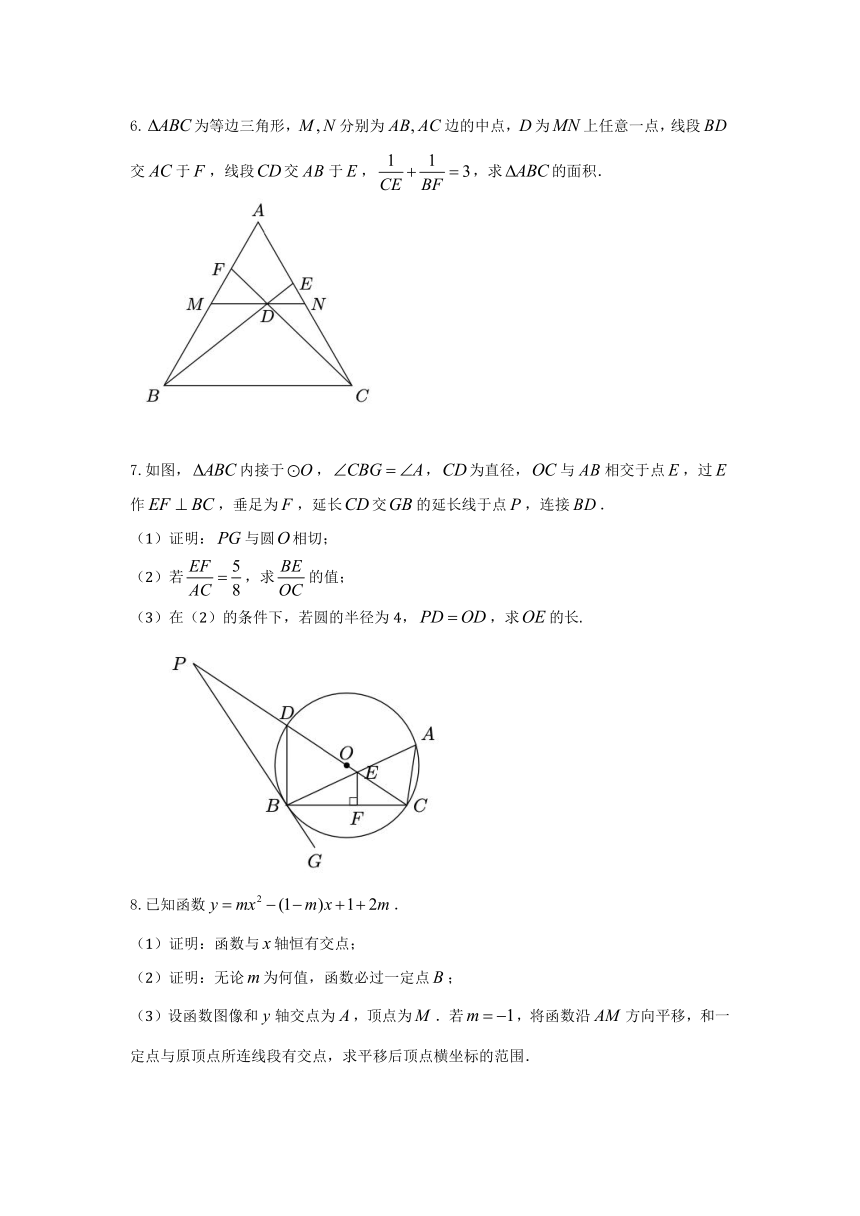
2.已知点,为轴上的一动点,为切线,已知圆半径为1,则的最小值为______.
3.,为该方程两根.则的值为______.
4.已知矩形,.为上一动点沿翻折,当为直角三角形时,则的周长为______.
5.点有一个无人机,一个人在点观测,离点45处点有一栋建筑物高,无人机水平向右以的速度飞行.
(1)无人机的高度为___________.
(2)无人机离开视线的时间为___________.
6.为等边三角形,分别为边的中点,为上任意一点,线段交于,线段交于,,求的面积.
7.如图,内接于,,为直径,与相交于点,过作,垂足为,延长交的延长线于点,连接.
(1)证明:与圆相切;
(2)若,求的值;
(3)在(2)的条件下,若圆的半径为4,,求的长.
8.已知函数.
(1)证明:函数与轴恒有交点;
(2)证明:无论为何值,函数必过一定点;
(3)设函数图像和轴交点为,顶点为.若,将函数沿方向平移,和一定点与原顶点所连线段有交点,求平移后顶点横坐标的范围.
9.某大学生创业,购进共300件,设的件数.的单价比的单价多6元.设,的总售价分别为函数.
与销售件数之间是一次函数的关系,如下表:
与之间的函数关系如图所示:
(1)直接写出与的函数关系;
(2)设销售两种商品所获利总利润为元,求与之间的函数解析式;
(3)大学生引进的300件商品全部售完,共获利350元,他计划每件商品捐给学校基金分别捐元,元, 捐款数恰好为总成本的,求的值.
10.对于大于1的奇数, 将其平方后拆分成2个相邻的整数, 这三个数为勾股数.
如:;;;
对于大于2的偶数,将其除以2再平方,将平方所得数分别加减1,这三个数为勾股数,如.
则以这种方法,12所得的勾股数中最大的数为__________.
11.证明:对于任意实数,求证:.
12.证明:
2022年西安交通大学少年班数学试题参考答案
1、7
2、
3、36
4、或6
5、(1)米 (2)秒
6、
7、(1)弦切角;(2);(3)
8、(1);(2)前系数为0的点
9、(1)
10、37
11、(1)设
当时,根据函数的性质,有
同理,对于上式也成立.
12、证明:此题可以利用等式,然后对的取值情况分类讨论证出,这里,我们通过构造辅助函数来处理.
作辅助函数
函数具有以下性质:对任意,均有
这表明,是一个以为周期的函数,又注意到对任意,中表达式内任意一项都为0,故。对任意,均有,这就是要证的结论
1.已知,则的值为______.
2.已知点,为轴上的一动点,为切线,已知圆半径为1,则的最小值为______.
3.,为该方程两根.则的值为______.
4.已知矩形,.为上一动点沿翻折,当为直角三角形时,则的周长为______.
5.点有一个无人机,一个人在点观测,离点45处点有一栋建筑物高,无人机水平向右以的速度飞行.
(1)无人机的高度为___________.
(2)无人机离开视线的时间为___________.
6.为等边三角形,分别为边的中点,为上任意一点,线段交于,线段交于,,求的面积.
7.如图,内接于,,为直径,与相交于点,过作,垂足为,延长交的延长线于点,连接.
(1)证明:与圆相切;
(2)若,求的值;
(3)在(2)的条件下,若圆的半径为4,,求的长.
8.已知函数.
(1)证明:函数与轴恒有交点;
(2)证明:无论为何值,函数必过一定点;
(3)设函数图像和轴交点为,顶点为.若,将函数沿方向平移,和一定点与原顶点所连线段有交点,求平移后顶点横坐标的范围.
9.某大学生创业,购进共300件,设的件数.的单价比的单价多6元.设,的总售价分别为函数.
与销售件数之间是一次函数的关系,如下表:
与之间的函数关系如图所示:
(1)直接写出与的函数关系;
(2)设销售两种商品所获利总利润为元,求与之间的函数解析式;
(3)大学生引进的300件商品全部售完,共获利350元,他计划每件商品捐给学校基金分别捐元,元, 捐款数恰好为总成本的,求的值.
10.对于大于1的奇数, 将其平方后拆分成2个相邻的整数, 这三个数为勾股数.
如:;;;
对于大于2的偶数,将其除以2再平方,将平方所得数分别加减1,这三个数为勾股数,如.
则以这种方法,12所得的勾股数中最大的数为__________.
11.证明:对于任意实数,求证:.
12.证明:
2022年西安交通大学少年班数学试题参考答案
1、7
2、
3、36
4、或6
5、(1)米 (2)秒
6、
7、(1)弦切角;(2);(3)
8、(1);(2)前系数为0的点
9、(1)
10、37
11、(1)设
当时,根据函数的性质,有
同理,对于上式也成立.
12、证明:此题可以利用等式,然后对的取值情况分类讨论证出,这里,我们通过构造辅助函数来处理.
作辅助函数
函数具有以下性质:对任意,均有
这表明,是一个以为周期的函数,又注意到对任意,中表达式内任意一项都为0,故。对任意,均有,这就是要证的结论
同课章节目录
