2022届高三数学二轮复习-三角函数的图象与性质课件(共20张PPT)
文档属性
| 名称 | 2022届高三数学二轮复习-三角函数的图象与性质课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 16:05:08 | ||
图片预览





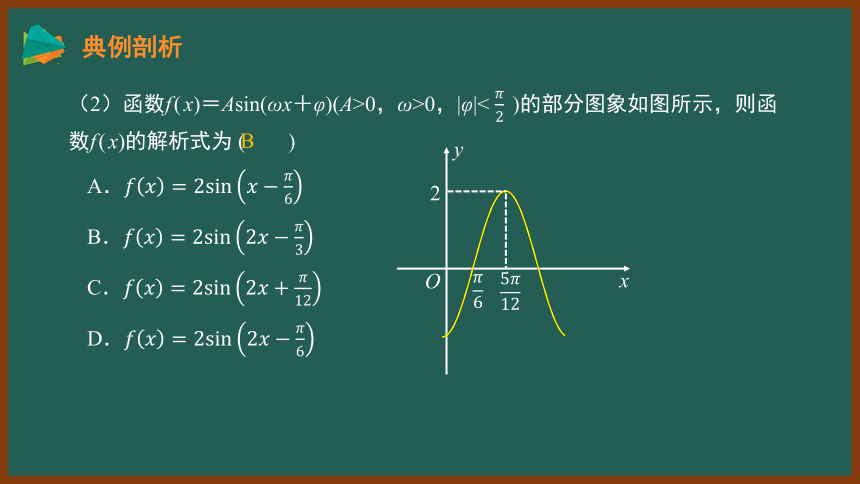


文档简介
(共20张PPT)
高三二轮复习
——《三角函数的图象与性质》
2.大题考法:利用三角函数的性质求解三角函数的值、参数、最值、值域、单调区间等,难度中等.
1.小题考法:三角函数图象变换、由图象确定解析式,难度中等.
考点1:三角函数的图象变换
(1)要想得到函数y=sin 2x+1的图象,只需将函数y=cos 2x的图象 ( )
A.向左平移个单位长度,再向上平移1个单位长度
B
B.向右平移个单位长度,再向上平移1个单位长度
C.向左平移个单位长度,再向下平移1个单位长度
D.向右平移个单位长度,再向下平移1个单位长度
三角函数图象平移问题处理的“三看”策略
一看平移要求
首先要看题目要求由哪个函数平移得到哪个函数,这是判断平移方向的关键点.
二看平移方向
平移的方向一般记为“正向左,负向右”,看y=Asin(ωx+φ)(ω>0)中φ的正负和它的平移要求.
三看平移单位
在函数y=Asin(ωx+φ)中,周期变换和相位变换都是沿x轴方向的,所以ω和φ之间有一定的关系, φ是初相,再经过ω的压缩,最后平移的单位是.
(2)函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< )的部分图象如图所示,则函数f(x)的解析式为 ( )
A.
B
B.
C.
D.
O
x
y
2
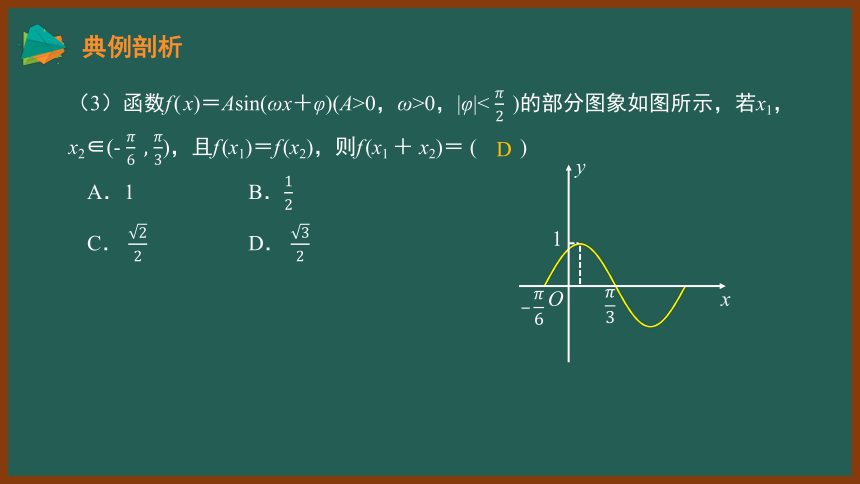
(3)函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< )的部分图象如图所示,若x1,x2∈(- ),且f(x1)=f(x2),则f(x1 + x2)= ( )
A.1 B.
D
C. D.
O
x
y
1
函数表达式 y=Asin(ωx+φ)+B 的确定方法
字母 确定途径 说明
A 由最值确定 A=
B 由最值确定 B=
ω 由函数的周期确定 相邻的最高点与最低点的横坐标之差的绝对值为半个周期,最高点(或最低点)的横坐标与相邻零点之差的绝对值为个周期,ω=.
φ 由图象上的特殊点确定 一般把第一个零点作为突破口,可以从图象的升降找准第一个零点的位置,利用待定系数法并结合图象列方程或方程组求解.
考点2:三角函数的性质
(1)函数,x∈[-1,1],则 ( )
A.f(x)为偶函数,且在[0,1]上单调递减
A
B.f(x)为偶函数,且在[0,1]上单调递增
C.f(x)为奇函数,且在[-1,0]上单调递增
D.f(x)为奇函数,且在[-1,0]上单调递减
求函数单调区间的方法
代换法
求形如y=Asin(ωx+φ)(或y=Acos(ωx+φ))(A,ω,φ为常数,A≠0,ω>0)的单调区间时,令ωx+φ=t,得y=Asin t(或y=Acos t),然后由复合函数的单调性求得.
图象法
画出三角函数的图象,结合图象求其单调区间.
(2)已知函数f(x)=sin xcos 2x,则下列关于函数 f(x)的结论中,错误的是 ( )
A.最大值为1
D
B.图象关于直线 x=对称
C.既是奇函数又是周期函数
D.图象关于点(,0)中心对称
判断函数对称性和对称轴的方法
利用函数y=Asin(ωx+φ)的对称轴一定经过图象的最高点或最低点,对称中心一定是函数的零点这一性质,通过检验f(x0)的值进行判断.
求三角函数周期常用结论
y=Asin(ωx+φ)和y=Acos(ωx+φ)的最小正周期为,y=tan(ωx+φ)的最小正周期为.
正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是个周期,相邻的对称中心与对称轴之间的距离是个周期;正切曲线相邻两对称中心之间的距离是个周期.
(3)已知函数 f(x)=sin(ωx+φ)(ω>0,|φ|< ) ,x=-为f(x)的零点, x=为y=f(x)图象的对称轴,且f(x)在( , )上单调,则ω的最大值为 ( )
A.11 B.9 C.7 D.5
B
考点3:三角函数的值域与最值
(1)函数f(x)=cos 2x+6cos(-x)的最大值为 ( )
A.4 B.5 C.6 D.7
B
(2)已知函数f(x)=sin(x+),其中x∈[- ,a],若f(x)的值域是[- ,1],则实数a的取值范围是________.
[
O
y
x
-
-
求三角函数值域的常见类型及方法
三角函数类型 求值域(最值)方法
y=asin x+bcos x+c 先化为y=Asin(ωx+φ)+k的形式,再求值域(最值)
y=asin2x+bsin x+c 可先设sin x=t,化为关于t的二次函数,再求值域
(最值)
y=asin xcos x+b(sin x±cos x)+c 可先设t=sin x±cos x,化为关于t的二次函数,再求值域(最值)
y= 一般可看成过定点的直线与圆上动点连线的斜率问题,利用数形结合求解
再见!
高三二轮复习
——《三角函数的图象与性质》
2.大题考法:利用三角函数的性质求解三角函数的值、参数、最值、值域、单调区间等,难度中等.
1.小题考法:三角函数图象变换、由图象确定解析式,难度中等.
考点1:三角函数的图象变换
(1)要想得到函数y=sin 2x+1的图象,只需将函数y=cos 2x的图象 ( )
A.向左平移个单位长度,再向上平移1个单位长度
B
B.向右平移个单位长度,再向上平移1个单位长度
C.向左平移个单位长度,再向下平移1个单位长度
D.向右平移个单位长度,再向下平移1个单位长度
三角函数图象平移问题处理的“三看”策略
一看平移要求
首先要看题目要求由哪个函数平移得到哪个函数,这是判断平移方向的关键点.
二看平移方向
平移的方向一般记为“正向左,负向右”,看y=Asin(ωx+φ)(ω>0)中φ的正负和它的平移要求.
三看平移单位
在函数y=Asin(ωx+φ)中,周期变换和相位变换都是沿x轴方向的,所以ω和φ之间有一定的关系, φ是初相,再经过ω的压缩,最后平移的单位是.
(2)函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< )的部分图象如图所示,则函数f(x)的解析式为 ( )
A.
B
B.
C.
D.
O
x
y
2
(3)函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< )的部分图象如图所示,若x1,x2∈(- ),且f(x1)=f(x2),则f(x1 + x2)= ( )
A.1 B.
D
C. D.
O
x
y
1
函数表达式 y=Asin(ωx+φ)+B 的确定方法
字母 确定途径 说明
A 由最值确定 A=
B 由最值确定 B=
ω 由函数的周期确定 相邻的最高点与最低点的横坐标之差的绝对值为半个周期,最高点(或最低点)的横坐标与相邻零点之差的绝对值为个周期,ω=.
φ 由图象上的特殊点确定 一般把第一个零点作为突破口,可以从图象的升降找准第一个零点的位置,利用待定系数法并结合图象列方程或方程组求解.
考点2:三角函数的性质
(1)函数,x∈[-1,1],则 ( )
A.f(x)为偶函数,且在[0,1]上单调递减
A
B.f(x)为偶函数,且在[0,1]上单调递增
C.f(x)为奇函数,且在[-1,0]上单调递增
D.f(x)为奇函数,且在[-1,0]上单调递减
求函数单调区间的方法
代换法
求形如y=Asin(ωx+φ)(或y=Acos(ωx+φ))(A,ω,φ为常数,A≠0,ω>0)的单调区间时,令ωx+φ=t,得y=Asin t(或y=Acos t),然后由复合函数的单调性求得.
图象法
画出三角函数的图象,结合图象求其单调区间.
(2)已知函数f(x)=sin xcos 2x,则下列关于函数 f(x)的结论中,错误的是 ( )
A.最大值为1
D
B.图象关于直线 x=对称
C.既是奇函数又是周期函数
D.图象关于点(,0)中心对称
判断函数对称性和对称轴的方法
利用函数y=Asin(ωx+φ)的对称轴一定经过图象的最高点或最低点,对称中心一定是函数的零点这一性质,通过检验f(x0)的值进行判断.
求三角函数周期常用结论
y=Asin(ωx+φ)和y=Acos(ωx+φ)的最小正周期为,y=tan(ωx+φ)的最小正周期为.
正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是个周期,相邻的对称中心与对称轴之间的距离是个周期;正切曲线相邻两对称中心之间的距离是个周期.
(3)已知函数 f(x)=sin(ωx+φ)(ω>0,|φ|< ) ,x=-为f(x)的零点, x=为y=f(x)图象的对称轴,且f(x)在( , )上单调,则ω的最大值为 ( )
A.11 B.9 C.7 D.5
B
考点3:三角函数的值域与最值
(1)函数f(x)=cos 2x+6cos(-x)的最大值为 ( )
A.4 B.5 C.6 D.7
B
(2)已知函数f(x)=sin(x+),其中x∈[- ,a],若f(x)的值域是[- ,1],则实数a的取值范围是________.
[
O
y
x
-
-
求三角函数值域的常见类型及方法
三角函数类型 求值域(最值)方法
y=asin x+bcos x+c 先化为y=Asin(ωx+φ)+k的形式,再求值域(最值)
y=asin2x+bsin x+c 可先设sin x=t,化为关于t的二次函数,再求值域
(最值)
y=asin xcos x+b(sin x±cos x)+c 可先设t=sin x±cos x,化为关于t的二次函数,再求值域(最值)
y= 一般可看成过定点的直线与圆上动点连线的斜率问题,利用数形结合求解
再见!
同课章节目录
