2022届高三数学二轮专题复习-数学应用与创新,数学文化课件(共34张PPT)
文档属性
| 名称 | 2022届高三数学二轮专题复习-数学应用与创新,数学文化课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 15:50:12 | ||
图片预览











文档简介
(共34张PPT)
数学应用与创新 数学文化
唐县第一中学高三实验部
教学目标:
1.学会用灵活,创新的思维能力进行发散性,求异性思考
2.寻找对材料内涵的解释和解决问题的办法
3掌握数学文化与高中知识的有机结合,对试题所提供的信息进行整理和分析
教学重难点:
1.用扎实的数学基础知识,良好的心态坦然面对新题型
2.感受数学思维方式,体验数学的理性精神
知识点回顾:
1.数列中的数学文化题一般以我国古代数学名著中的等差数列和等比数列问题为背景,考查等差数列和等比数列的概念、通项公式和前n项和公式.
2.立体几何中的数学文化题一般以我国古代发现的球的体积公式、圆柱的体积公式、圆锥的体积公式、圆台的体积公式和“牟合方盖”“阳马”“鳖臑”“堑堵”等中国古代几何名词为背景考查空间几何体的体积与表面积等.
3.三角函数中的数学文化题一般以我国古代数学名著中的几何测量问题或几何图形为背景,考查解三角形或三角变换.
新型题:
1.“新运算”是指在现有的运算法则和运算律的基础上定义的一种新的运算,是一种特别设计的计算形式,它使用一些特殊的运算符号,如“x”“②”“※”等,这些符号与四则运算中的加减乘除符号是不一样的.“新运算”类问题的情境一般比较陌生,求解时需要坦然面对,先准确理解“新运算”法则,再加以灵活运用即可解决问题.特别注意:新定义的算式在没有转化前,是不适合运用现有的运算法则和运算律进行计算的.
2.“新定义”试题是指给出一个未接触过的新规定、新概念,要求现学现用,其目的是考查阅读理解能力、应变能力和创新能力,培养学生自主学习、主动探究的品质.此类型问题可能以文字的形式出现,也可能以数学符号或数学表达式的形式出现,要求先准确理解“新定义”的特点,再加以灵活运用.特别提醒:“给什么,用什么”是应用“新定义”解题的基本思路.
3.“新模型”试题指已知条件中给出具体的解题模型,需要学生将所给解题模型迁移至新情境中,对目标问题进行合理探究.此类型问题要求学生现学现用,着重考查学生的阅读理解能力,接受能力,应变能力和创新、探究能力,有利于培养学生养成善于思考、勤于钻研的好习惯.特别提醒:紧扣“新模型”的思维本质,是解题的基本原则.
例题分析:
例1:
答案:
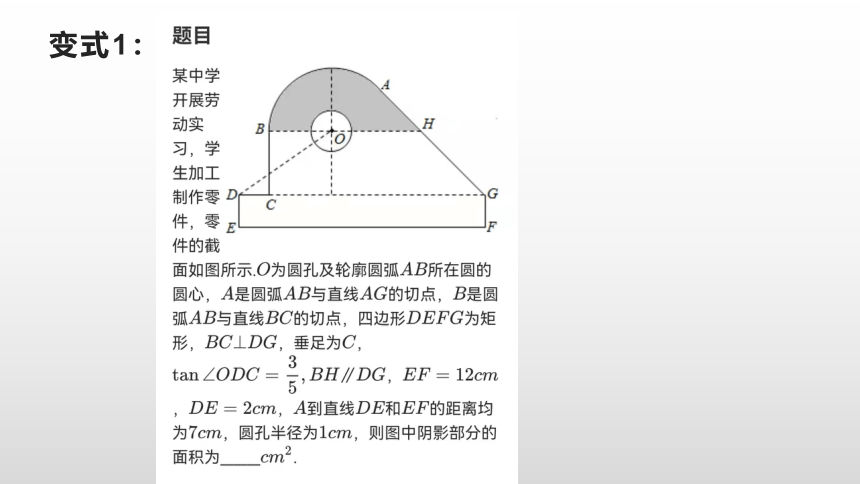
变式1:
例2:
变式2:
例3:
变式3
答案:
例4:1
2.
3、
4.
例5:1
2、
例6:
课堂小结:
解决数学文化问题的关键:
(1)读懂题意.“脱去”数学文化的背景,提取关键信息
(2)构建模型.由题意构建数列、立体几何、三角、概率等模型.
(3)求解模型.把文字语言转化为相关信息,解答问题.
创新情境问题注重对所学数学知识、方法的有效整合,侧重考查学生的综合运用能力.此类型问题的设置充分体现了考纲要求——对数学基础知识的考查,注重学科的内在联系和知识的综合性,在知识网络的交汇点处设计试题,使对数学基础知识的考查达到必要的深度;对数学能力的考查,强调“以能力立意”,侧重体现对知识的理解和应用,尤其是综合和灵活的应用,以此来检测考生将知识迁移到不同情境中去的能力,从而检测出学生的理性思维的广度和深度以及进一步学习的潜能。
谢 谢
数学应用与创新 数学文化
唐县第一中学高三实验部
教学目标:
1.学会用灵活,创新的思维能力进行发散性,求异性思考
2.寻找对材料内涵的解释和解决问题的办法
3掌握数学文化与高中知识的有机结合,对试题所提供的信息进行整理和分析
教学重难点:
1.用扎实的数学基础知识,良好的心态坦然面对新题型
2.感受数学思维方式,体验数学的理性精神
知识点回顾:
1.数列中的数学文化题一般以我国古代数学名著中的等差数列和等比数列问题为背景,考查等差数列和等比数列的概念、通项公式和前n项和公式.
2.立体几何中的数学文化题一般以我国古代发现的球的体积公式、圆柱的体积公式、圆锥的体积公式、圆台的体积公式和“牟合方盖”“阳马”“鳖臑”“堑堵”等中国古代几何名词为背景考查空间几何体的体积与表面积等.
3.三角函数中的数学文化题一般以我国古代数学名著中的几何测量问题或几何图形为背景,考查解三角形或三角变换.
新型题:
1.“新运算”是指在现有的运算法则和运算律的基础上定义的一种新的运算,是一种特别设计的计算形式,它使用一些特殊的运算符号,如“x”“②”“※”等,这些符号与四则运算中的加减乘除符号是不一样的.“新运算”类问题的情境一般比较陌生,求解时需要坦然面对,先准确理解“新运算”法则,再加以灵活运用即可解决问题.特别注意:新定义的算式在没有转化前,是不适合运用现有的运算法则和运算律进行计算的.
2.“新定义”试题是指给出一个未接触过的新规定、新概念,要求现学现用,其目的是考查阅读理解能力、应变能力和创新能力,培养学生自主学习、主动探究的品质.此类型问题可能以文字的形式出现,也可能以数学符号或数学表达式的形式出现,要求先准确理解“新定义”的特点,再加以灵活运用.特别提醒:“给什么,用什么”是应用“新定义”解题的基本思路.
3.“新模型”试题指已知条件中给出具体的解题模型,需要学生将所给解题模型迁移至新情境中,对目标问题进行合理探究.此类型问题要求学生现学现用,着重考查学生的阅读理解能力,接受能力,应变能力和创新、探究能力,有利于培养学生养成善于思考、勤于钻研的好习惯.特别提醒:紧扣“新模型”的思维本质,是解题的基本原则.
例题分析:
例1:
答案:
变式1:
例2:
变式2:
例3:
变式3
答案:
例4:1
2.
3、
4.
例5:1
2、
例6:
课堂小结:
解决数学文化问题的关键:
(1)读懂题意.“脱去”数学文化的背景,提取关键信息
(2)构建模型.由题意构建数列、立体几何、三角、概率等模型.
(3)求解模型.把文字语言转化为相关信息,解答问题.
创新情境问题注重对所学数学知识、方法的有效整合,侧重考查学生的综合运用能力.此类型问题的设置充分体现了考纲要求——对数学基础知识的考查,注重学科的内在联系和知识的综合性,在知识网络的交汇点处设计试题,使对数学基础知识的考查达到必要的深度;对数学能力的考查,强调“以能力立意”,侧重体现对知识的理解和应用,尤其是综合和灵活的应用,以此来检测考生将知识迁移到不同情境中去的能力,从而检测出学生的理性思维的广度和深度以及进一步学习的潜能。
谢 谢
同课章节目录
