北师大版九年级数学下册第二章二次函数综合练习 (Word版,附答案解析)
文档属性
| 名称 | 北师大版九年级数学下册第二章二次函数综合练习 (Word版,附答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 180.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 21:00:55 | ||
图片预览




文档简介
北师大版九年级数学下册第2章《二次函数》综合练习
一、单选题
1.抛物线y=(x+2)2+3的顶点坐标是( )
A.(﹣2,﹣3) B.(﹣2,3)
C.(2,﹣3) D.(2,3)
2.二次函数 有( )
A.最大值 B.最小值 C.最大值 D.最小值
3.抛物线 的对称轴是( )
A. B. C. D.
4.二次函数y=3x2+1和y=3(x﹣1)2 , 以下说法:
①它们的图象都是开口向上;
②它们的对称轴都是y轴,顶点坐标都是原点(0,0);
③当x>0时,它们的函数值y都是随着x的增大而增大;
④它们的开口的大小是一样的.
其中正确的说法有( )
A.1个 B.2 C.3 D.4个
5.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①抛物线的对称轴为x=﹣1;②abc=0;③方程ax2+bx+c+1=0有两个不相等的实数根;④无论x取何值,ax2+bx≤a﹣b.其中,正确的个数为( )
A.4 B.3 C.2 D.1
6.已知二次函数 ,当自变量x分别取-2,2,5时,对应的值分别为 ,则 的大小关系正确的是( )
A. B. C. D.
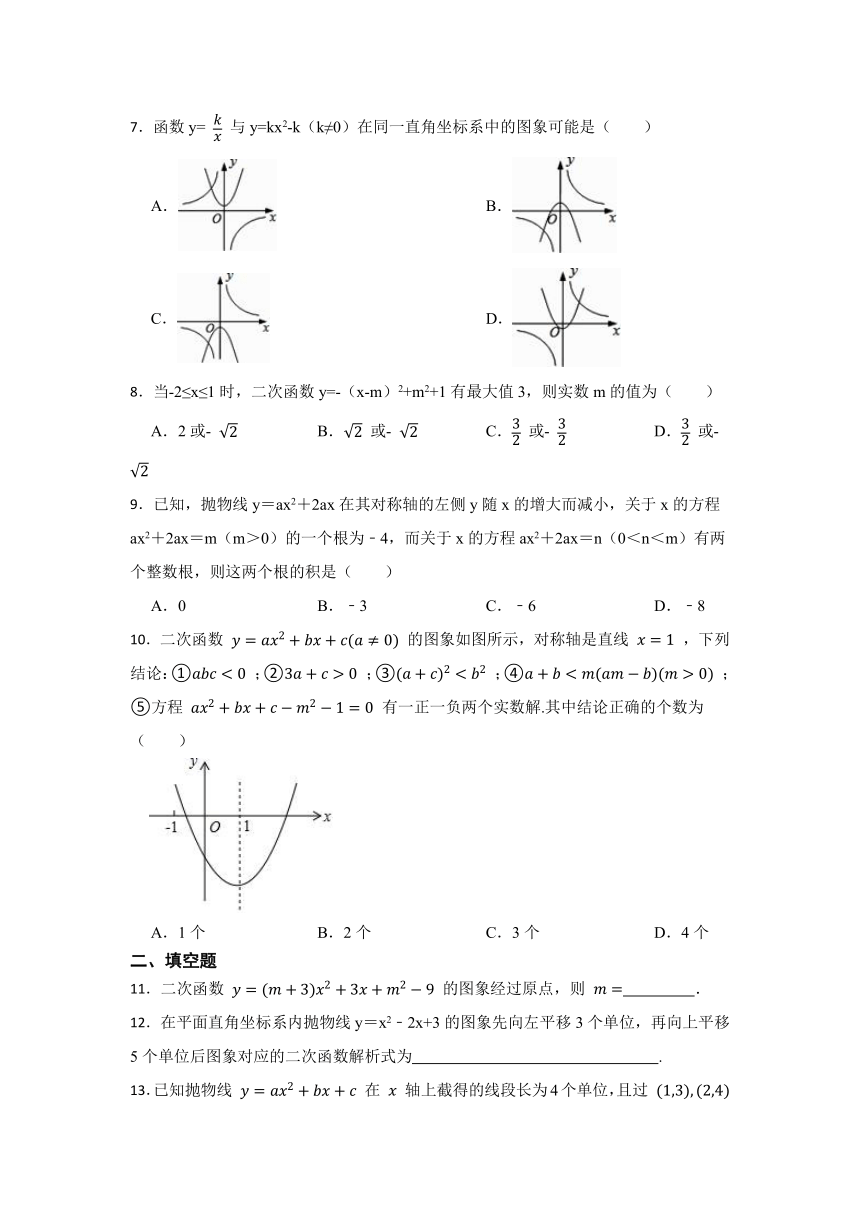
7.函数y= 与y=kx2-k(k≠0)在同一直角坐标系中的图象可能是( )
A. B.
C. D.
8.当-2≤x≤1时,二次函数y=-(x-m)2+m2+1有最大值3,则实数m的值为( )
A.2或- B. 或- C. 或- D. 或-
9.已知,抛物线y=ax2+2ax在其对称轴的左侧y随x的增大而减小,关于x的方程ax2+2ax=m(m>0)的一个根为﹣4,而关于x的方程ax2+2ax=n(0<n<m)有两个整数根,则这两个根的积是( )
A.0 B.﹣3 C.﹣6 D.﹣8
10.二次函数 的图象如图所示,对称轴是直线 ,下列结论:① ;② ;③ ;④ ;⑤方程 有一正一负两个实数解.其中结论正确的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.二次函数 的图象经过原点,则 .
12.在平面直角坐标系内抛物线y=x2﹣2x+3的图象先向左平移3个单位,再向上平移5个单位后图象对应的二次函数解析式为 .
13.已知抛物线 在 轴上截得的线段长为4个单位,且过 两点,则 = .
14.如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧,其图象与x轴交于点A(﹣1,0)与点C(x2,0),且与y轴交于点B(0,﹣2),小强得到以下结论:①0<a<2;②﹣1<b<0;③c=﹣1;④当|a|=|b|时x2> ﹣1;以上结论中正确结论的序号为 .
15.某校购买了一套乒乓球桌和自动发球机,侧面如图1所示,球台长度AB=274cm,发球机紧贴球台端线点A处,高出球台的部分AC=12cm,出球管道CD=5 cm,若将水平状态的CD绕点C逆时针旋转45°到CD的位置,发球机模式为“一跳球",路线呈抛物线,离球台正中间的球网GH左侧72cm处到达最高点高出台面21cm,则EB= cm
16.如图,在平面直角坐标系 xOy 中,已知 A 是抛物线 y=2x2+bx 上一点,顶点 B 的横坐标是1,当△AOB 是直角三角形时,点 A 的坐标为 .
三、解答题
17.已知抛物线y=﹣2x2+(m﹣3)x﹣8.
(1)若抛物线的对称轴为y轴,求m的值;
(2)若抛物线的顶点在x正半轴上,求m的值.
18.二次函数图像的顶点坐标是(-2,3),并经过点(1,2),求这个二次函数的函数关系式.
19. 已知二次函数的图象经过,两点,求b,c的值.
20.某商店购进一批单价为20元的日用商品,如果以单价30元销售,那么半月内可售出400件,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件,如果提高售价,请问将售价定每件为多少元时,才能在半月内获得最大利润?并求出最大利润.
21.如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)求抛物线的表达式;
(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;
(3)如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
22.如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=﹣ x2+ x+4经过A、B两点.
(1)写出点A、点B的坐标;
(2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连接PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;
(3)在(2)的条件下,是否存在t,使得△PAM是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
答案解析部分
1.【答案】B
【解析】【解答】解:二次函数y=(x+2)2+3的图象的顶点坐标为(﹣2,3).
故答案为:B.
【分析】根据二次函数的解析式求解即可。
2.【答案】C
【解析】【解答】解:由二次函数 可得: ,
∵ ,
∴当x=1时,二次函数有最大值为-4;
故答案为:C.
【分析】由二次函数 中,a=-1<0,可得抛物线开口向下,函数存在最大值,利用二次函数的性质求出其最大值即可.
3.【答案】A
【解析】【解答】解:∵ ,
∴对称轴为直线x=- ,
故答案为:A.
【分析】抛物线(a≠0)的对称轴为直线x=,据此计算即可.
4.【答案】B
【解析】【解答】解:①因为a=3>0,它们的图象都是开口向上,此说法正确;
② 对称轴是y轴,顶点坐标是(0,1), 的对称轴是x=1,顶点坐标是(1,0),此说法错误;
③二次函数 ,当x>0时,y随着x的增大而增大; 当 时,y随着x的增大而增大;此说法错误;
④因为a=3,所以它们的开口的大小是一样的,此选项正确.
综上所知,正确的有①④两个.
故答案为:B.
【分析】①由两个二次函数的解析式可得a=3>0,于是可得这两个二次函数的图象的开口向上;
②由抛物线y=3x2+1可知其对称轴是y轴,顶点坐标是(0,1);由抛物线y=3(x-1)2可知其对称轴是x=1,顶点坐标是(1,0);
③结合②的结论可知:抛物线y=3x2+1,当x>0时,y随着x的增大而增大;抛物线y=3(x-1)2,当 时,y随着x的增大而增大;
④由两个二次函数的解析式可得a=3,于是可得它们的开口的大小是一样的.
5.【答案】A
【解析】【解答】解:∵抛物线与x轴的交点坐标为(﹣2,0),(0,0),
∴对称轴为x= =﹣1,故①正确;
∵抛物线开口向下,a<0,抛物线与原点相交,c=0,
∴abc=0,故②正确;
∵c=0,
∴b2﹣4a(c+1)=b2﹣4a>0,故③正确;
当x=﹣1时,抛物线有最大值,
∴无论x取何值,ax2+bx+c≤a﹣b+c,
即ax2+bx≤a﹣b,故④正确.
正确的为①②③④,
故答案为:A.
【分析】根据抛物线与x轴两交点的坐标,及抛物线的对称性即可得出其对称轴直线是x=-1,故①正确;抛物线开口向下,a<0,抛物线与原点相交,c=0,抛物线的对称轴在y轴的左侧,故a,b同号,从而得出b<0,故abc=0,故②正确;算出方程 ax2+bx+c+1=0 的根的判别式的值,由判别式的值大于0,得出该方程 有两个不相等的实数根 ,故③正确;当x=﹣1时,抛物线有最大值,故无论x取何值,ax2+bx+c≤a﹣b+c,即ax2+bx≤a﹣b,故④正确,综上所述即可得出答案。
6.【答案】C
【解析】【解答】解:由二次函数 知,二次函数的开口向上,对称轴为直线x=2,
又-2对应的点离对称轴最远,2对应的点离对称轴最近,
∴
故答案为:C.
【分析】根据二次函数的图象开口向上,则离对称轴越远的点的函数值越大即可解答.
7.【答案】D
【解析】【解答】由解析式y=-kx2+k可得:抛物线对称轴x=0;
选项A,由双曲线的两支分别位于二、四象限,可得k<0,则-k>0,抛物线开口方向向上、抛物线与y轴的交点为y轴的负半轴上;本图象与k的取值相矛盾,选项A不符合题意;
选项B,由双曲线的两支分别位于一、三象限,可得k>0,则-k<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象与k的取值相矛盾,选项B不符合题意;
选项C,由双曲线的两支分别位于一、三象限,可得k>0,则-k<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的负半轴上,本图象与k的取值相矛盾,选项C不符合题意;
选项D,由双曲线的两支分别位于一、三象限,可得k>0,则-k<0,抛物线开口方向向上、抛物线与y轴的交点在y轴的负半轴上,本图象与k的取值相矛盾,选项D符合题意.
故答案为:D.
【分析】先由反比例函数的图象得到字母系数的正负,再与二次函数的图象相比较看是否一致,由此即可解答.
8.【答案】D
【解析】【解答】二次函数y=-(x-m)2+m2+1,
可化为:y=-x2+2mx+1,
故二次函数的对称轴为直线x=m,
①m<-2时,x=-2时二次函数有最大值,
此时-(-2-m)2+m2+1=3,
解得m=- ,与m<-2矛盾,故m值不存在;
②当-2≤m≤1时,x=m时,二次函数有最大值,
此时,m2+1=3,
解得m=- ,m= (舍去);
③当m>1时,x=1时二次函数有最大值,
此时,-(1-m)2+m2+1=3,
解得m= .
综上所述,m的值为 或- .
故答案为:D.
【分析】求出二次函数对称轴为直线x=m,再分m<-2,-2≤m≤1,m>1三种情况,根据二次函数的增减性列方程求解即可.
9.【答案】B
【解析】【解答】抛物线y=ax2+2ax的对称轴为直线x=﹣ =﹣1,
∵抛物线y=ax2+2ax在其对称轴的左侧y随x的增大而减小,
∴a>0,抛物线的开口向上,
当y=0时,ax2+2ax=0,解得 ,
即抛物线y=ax2+2ax与x轴的交点坐标为 ,如图所示:
∵关于x的方程ax2+2ax=m(m>0)的一个根为﹣4,
∴关于x的方程ax2+2ax=m(m>0)的另一个根为2,
∵关于x的方程ax2+2ax=n(0<n<m)有两个整数根,
∴关于x的方程ax2+2ax=n(0<n<m)有两个整数根只能为 ,
∴这两个根的积是为﹣3.
故答案为:B.
【分析】 先求得抛物线y=ax2+2ax的对称轴,开口向上,利用抛物线的对称性得到方程ax2+2ax=m的另一个根,利用图象法得到方程ax2+2ax=n的两个整数根,即可求出这两个根的积.
10.【答案】D
【解析】【解答】解:①∵抛物线开口向上,∴a>0,
∵抛物线的对称轴在y轴右侧,∴b<0
∵抛物线与y轴交于负半轴,
∴c<0,
∴abc>0,①不符合题意;
②当x= 1时,y>0,∴a b+c>0,
∵ =1,∴b= 2a,
把b= 2a代入a b+c>0中得3a+c>0,所以②符合题意;
③当x=1时,y<0,∴a+b+c<0,
∴a+c< b,
当x= 1时,y>0,∴a b+c>0,
∴a+c>b,
∴|a+c|<|b|
∴(a+c)2<b2,所以③符合题意;
④∵抛物线的对称轴为直线x=1,
∴x=1时,函数的最小值为a+b+c,
∵ ,∴-m<0,
由图像可知,当x=-m时,y>a+b+c,
∴ ,④符合题意.
⑤令y2= ,则y2≥1,根据函数图像可得交点的横坐标为一正一负,故方程 有一正一负两个实数解,符合题意.
故答案为:D.
【分析】①由抛物线开口方向得到a>0,对称轴在y轴右侧,得到a与b异号,又抛物线与y轴正半轴相交,得到c<0,可得出abc>0,选项①不符合题意;
②把b= 2a代入a b+c>0中得3a+c>0,所以②符合题意;
③由x=1时对应的函数值y<0,可得出a+b+c<0,得到a+c< b,x= 1时,y>0,可得出a b+c>0,得到|a+c|<|b|,即可得到(a+c)2 b2<0,选项③符合题意;
④由对称轴为直线x=1,即x=1时,y有最小值,可得结论,即可得到④符合题意.
⑤令y2= ,则y2≥1,根据函数图像可得交点的横坐标为一正一负,故可判断⑤.
11.【答案】3
【解析】【解答】解:根据二次函数图象过原点,把 代入解析式,
得 ,整理得 ,解得 ,
∵ ,
∴ ,
∴ .
故答案为:3.
【分析】先求出,再求出,最后计算求解即可。
12.【答案】y=(x+2)2+7或y=x2+4x+11
【解析】【解答】解:二次函数y=x2﹣2x+3=(x﹣1)2+2的图象在坐标平面内向左平移3个单位,再向上平移5个单位后图象对应的二次函数解析式为y=(x﹣1+3)2+2+5,即y=(x+2)2+7或y=x2+4x+11.
故答案为:y=(x+2)2+7或y=x2+4x+11(两种形式都可以).
【分析】根据抛物线的平移规律“左加右减、上加下减”可求解.
13.【答案】
【解析】【解答】解:由题意可知:
解得:或.
故答案为: .
【分析】将点 代入 抛物线 得出两个方程,再根据抛物线在x轴上截得的线段长为4,列出第三个方程,然后解这三个方程组成的方程组即可求出a的值.
14.【答案】①④
【解析】【解答】由A(﹣1,0),B(0,﹣2),得b=a﹣2,
∵开口向上,
∴a>0;
∵对称轴在y轴右侧,
∴﹣ >0,
∴﹣ >0,
∴a﹣2<0,
∴a<2;
∴0<a<2;
∴①符合题意;
∵抛物线与y轴交于点B(0,﹣2),
∴c=﹣2,故③不符合题意;
∵抛物线图象与x轴交于点A(﹣1,0),
∴a﹣b﹣2=0,无法得到0<a<2;②﹣1<b<0,故①②不符合题意;
∵|a|=|b|,二次函数y=ax2+bx+c的对称轴在y轴的右侧,
∴二次函数y=ax2+bx+c的对称轴为y= ,
∴x2=2> ﹣1,故④符合题意.
故答案为①④.
【分析】根据抛物线与y轴交于点B(0,-2),可得c=-2,依此判断③;由抛物线图象与x轴交于点A(-1,0),可得a-b-2=0,依此判断①②;由|a|=|b|可得二次函数y=ax2+bx+c的对称轴为x= ,可得x2=2,比较大小即可判断④;从而求解.
15.【答案】209-30
【解析】【解答】解:以AC为y轴,AB为x轴,A为原点建立坐标系,过点D'作D'P⊥x轴交CD于点Q,交x轴于点P,如图所示:
∵ 正中间的球网GH,
∴,
∵点N在离球台正中间的球网GH左侧72cm处到达最高点高出台面21cm,
∴AM=AH-MH=137-72=65,NM=21,
∴设抛物线的解析式为y=a(x-65)2+21,
由旋转得,,
∴在Rt△D'CQ中,CQ=D'Q=5,
∴D'(5,17),
把D'代入y=a(x-65)2+21得,
∴,
当y=0时,,
解得,(不合题意,舍去),
∴,
故答案为:.
【分析】以AC为y轴,AB为x轴,A为原点建立坐标系,过点D'作D'P⊥x轴交CD于点Q,交x轴于点P,易得点N的坐标,再设抛物线的解析式为y=a(x-65)2+21,由旋转的性质结合特殊三角函数的值即可求出点D'的坐标,将D'代入函数解析式即可求出抛物线解析式,进而令y=0,解出x,再由即可求解.
16.【答案】 或 或
【解析】【解答】解:∵顶点 B 的横坐标是1,
解之:b=-4
∴抛物线的解析式为:y=2x2-4x=-2(x-1)2+2,
∴点B(1,2)
设点A(m,2m2-4m),
∴OA2=m2+(2m2-4m)2,OB2=22+1=5,AB2=(m-1)2+(2m2-4m+2)2
当AB2+OB2=OA2时
∴(m-1)2+(2m2-4m+2)2+5=m2+(2m2-4m)2,
整理得:4m2-9m+5=0
解之:m1=,m2=1(舍去),
∴2m2-4m=
∴点A;
当∠OAB=90°时,过点A作AN⊥x轴于点N,过点B作EM⊥y轴于点E,交NA的延长线于点M,
∴∠ONA=∠AMB=90°,
∴∠BAM+∠ABM=90°,∠NAO+∠BAM=90°,
∴∠ABM=∠NAO,
∴△NAO∽△ABM,
∴
设ON=a,NA=c,
∴AM=2-c,BM=a-1,点A(a,-c)
∴-c=2a2-4a,
∴
∴a2-a=2c-c2,
解之:
∴点A();
当OB2+OA2=AB2时,
5+m2+(2m2-4m)2=(m-1)2+(2m2-4m+2)2,
整理得:4m2-9m=0
解之:m1=,m2=0
当m=时,2m2-4m=
∴点A .
∴点A或或.
故答案为:或(或.
【分析】利用顶点的横坐标为1,可求出b的值,即可得到函数解析式,利用函数解析式求出顶点B的坐标;设点A(m,2m2-4m),利用勾股定理分别表示出AB2、OB2、OA2,利用勾股定理分情况讨论:当AB2+OB2=OA2时;当OB2+OA2=AB2时;分别建立关于m的方程,解方程求出符合题意的m的值,即可得到点A的坐标;当∠OAB=90°时,过点A作AN⊥x轴于点N,过点B作EM⊥y轴于点E,交NA的延长线于点M,易证△NAO∽△ABM,利用全等三角形的性质可得对应边成比例,设ON=a,NA=c,可表示出AM,BM的长,同时可得到点A的坐标,将点A的坐标代入函数解析式,可得到关于a,c的方程组,解方程组求出a,c的值,可得点A的坐标;综上所述可得到符合题意的点A的坐标.
17.【答案】(1)解:∵抛物线y=﹣2x2+(m﹣3)x﹣8的对称轴为y轴,
∴﹣ =0,
解得,m=3,即m的值是3;
(2)解:∵抛物线y=﹣2x2+(m﹣3)x﹣8的顶点在x正半轴上,
∴ ,
解得m=11, 即m的值是11.
【解析】【分析】(1)根据对称轴公式 即可求m的值;(2)根据顶点坐标公式求解即可.
18.【答案】解:设二次函数解析式为y=a(x+2)2+3,
把(1,2)代入得9a+3=2,解得a= ,
所以二次函数解析式为:y= (x+2)2+3.
【解析】【分析】利用顶点式,利用待定系数法求解二次函数解析式即可。
19.【答案】解:把A(0,3) ,B(-4,-) 分别代入,
得,
解得.
故,c=3.
【解析】【分析】将点A、B的坐标代入求解就可得到b、c的值.
20.【答案】解:设售价定每件为 元,利润为 元,依题意可得
,
整理得 ,
配方得 ,
∵-20<0,
∴当 时, 的最大值为4500元.
答:售价定为每件35元时,才能在半月内获得最大利润,最大利润为4500元.
【解析】【分析】 设售价定每件为 元,利润为 元,根据“利润=单件利润×销售量”求得函数关系式,然后利用二次函数的性质求最大值即可.
21.【答案】(1)将点A(-1,0),B(4,0)的坐标代入函数的表达式得:
,
解得:b=3,c=4.
抛物线的解析式为y=-x2+3x+4.
(2)如图1所示: ∵令x=0得y=4, ∴OC=4.
∴OC=OB.
∵∠CFP=∠COB=90°, ∴FC=PF时,以P,C,F为顶点的三角形与△OBC相似.
设点P的坐标为(a,-a2+3a+4)(a>0).
则CF=a,PF=|-a2+3a+4-4|=|a2-3a|.
∴|a2-3a|=a.
解得:a=2,a=4.
∴点P的坐标为(2,6)或(4,0).
(3)如图2所示:连接EC. 设点P的坐标为(a,-a2+3a+4).则OE=a,PE=-a2+3a+4,EB=4-a.
∵S四边形PCEB= OB PE= ×4(-a2+3a+4),S△CEB= EB OC= ×4×(4-a),
∴S△PBC=S四边形PCEB-S△CEB=2(-a2+3a+4)-2(4-a)=-2a2+8a.
∵a=-2<0,
∴当a=2时,△PBC的面积S有最大值.
∴P(2,6),△PBC的面积的最大值为8.
【解析】【分析】(1)抛物线过AB两点,将两点坐标代入即可求出bc 的值,从而得到抛物线表达式。
(2)已知抛物线函数表达式,即可求出与y轴交点点C的坐标。得OC=OB。△COB是等腰三角形。若要△CPF∽△CBO,故△CPF是等腰三角形。即CF=PF。从而求出点P的坐标。
(3) 设点P的坐标为(a,-a2+3a+4) ,将各边表示出来。然后分别写出四边形PCEB的面积公式以及三角形CEB的面积公式,即可将三角形PBC的面积表示出来。即可求出a 的取值。
22.【答案】(1)解:抛物线y=﹣0.5x2+3.5x+4中:令x=0,y=4,则 B(0,4);
令y=0,0=﹣0.5x2+3.5x+4,解得 x1=﹣1、x2=8,则 A(8,0);∴A(8,0)、B(0,4).
(2)解:△ABC中,AB=AC,AO⊥BC,则OB=OC=4,∴C(0,﹣4).
由A(8,0)、B(0,4),得:直线AB:y=﹣0.5x+4;
依题意,知:OE=2t,即 E(2t,0);
∴P(2t,﹣2t2+7t+4)、Q(2t,﹣t+4),PQ=(﹣2t2+7t+4)﹣(﹣t+4)=﹣2t2+8t;
S=S△ABC+S△PAB=0.5×8×8+0.5×(﹣2t2+8t)×8=﹣8t2+32t+32=﹣8(t﹣2)2+64;
∴当t=2时,S有最大值,且最大值为64.
(3)解:∵PM∥y轴,∴∠AMP=∠ACO<90°;
而∠APM是锐角,所以△PAM若是直角三角形,只能是∠PAM=90°;
由A(8,0)、C(0,﹣4),得:直线AC:y=0.5x﹣4;
所以,直线AP可设为:y=﹣2x+h,代入A(8,0),得:﹣16+h=0,h=16
∴直线AP:y=﹣2x+16,联立抛物线的解析式,∴存在符合条件的点P,且坐标为(3,10).
【解析】【分析】(1)抛物线的解析式中,令x=0,能确定点B的坐标;令y=0,能确定点A的坐标.(2)四边形PBCA可看作△ABC、△PBA两部分;△ABC的面积是定值,关键是求出△PBA的面积表达式;若设直线l与直线AB的交点为Q,先用t表示出线段PQ的长,而△PAB的面积可由( PQ OA)求得,在求出S、t的函数关系式后,由函数的性质可求得S的最大值.(3)△PAM中,∠APM是锐角,而PM∥y轴,∠AMP=∠ACO也不可能是直角,所以只有∠PAC是直角一种可能,即 直线AP、直线AC垂直,此时两直线的斜率乘积为-1,先求出直线AC的解析式,联立抛物线的解析式后可求得点P的坐标
一、单选题
1.抛物线y=(x+2)2+3的顶点坐标是( )
A.(﹣2,﹣3) B.(﹣2,3)
C.(2,﹣3) D.(2,3)
2.二次函数 有( )
A.最大值 B.最小值 C.最大值 D.最小值
3.抛物线 的对称轴是( )
A. B. C. D.
4.二次函数y=3x2+1和y=3(x﹣1)2 , 以下说法:
①它们的图象都是开口向上;
②它们的对称轴都是y轴,顶点坐标都是原点(0,0);
③当x>0时,它们的函数值y都是随着x的增大而增大;
④它们的开口的大小是一样的.
其中正确的说法有( )
A.1个 B.2 C.3 D.4个
5.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①抛物线的对称轴为x=﹣1;②abc=0;③方程ax2+bx+c+1=0有两个不相等的实数根;④无论x取何值,ax2+bx≤a﹣b.其中,正确的个数为( )
A.4 B.3 C.2 D.1
6.已知二次函数 ,当自变量x分别取-2,2,5时,对应的值分别为 ,则 的大小关系正确的是( )
A. B. C. D.
7.函数y= 与y=kx2-k(k≠0)在同一直角坐标系中的图象可能是( )
A. B.
C. D.
8.当-2≤x≤1时,二次函数y=-(x-m)2+m2+1有最大值3,则实数m的值为( )
A.2或- B. 或- C. 或- D. 或-
9.已知,抛物线y=ax2+2ax在其对称轴的左侧y随x的增大而减小,关于x的方程ax2+2ax=m(m>0)的一个根为﹣4,而关于x的方程ax2+2ax=n(0<n<m)有两个整数根,则这两个根的积是( )
A.0 B.﹣3 C.﹣6 D.﹣8
10.二次函数 的图象如图所示,对称轴是直线 ,下列结论:① ;② ;③ ;④ ;⑤方程 有一正一负两个实数解.其中结论正确的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.二次函数 的图象经过原点,则 .
12.在平面直角坐标系内抛物线y=x2﹣2x+3的图象先向左平移3个单位,再向上平移5个单位后图象对应的二次函数解析式为 .
13.已知抛物线 在 轴上截得的线段长为4个单位,且过 两点,则 = .
14.如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧,其图象与x轴交于点A(﹣1,0)与点C(x2,0),且与y轴交于点B(0,﹣2),小强得到以下结论:①0<a<2;②﹣1<b<0;③c=﹣1;④当|a|=|b|时x2> ﹣1;以上结论中正确结论的序号为 .
15.某校购买了一套乒乓球桌和自动发球机,侧面如图1所示,球台长度AB=274cm,发球机紧贴球台端线点A处,高出球台的部分AC=12cm,出球管道CD=5 cm,若将水平状态的CD绕点C逆时针旋转45°到CD的位置,发球机模式为“一跳球",路线呈抛物线,离球台正中间的球网GH左侧72cm处到达最高点高出台面21cm,则EB= cm
16.如图,在平面直角坐标系 xOy 中,已知 A 是抛物线 y=2x2+bx 上一点,顶点 B 的横坐标是1,当△AOB 是直角三角形时,点 A 的坐标为 .
三、解答题
17.已知抛物线y=﹣2x2+(m﹣3)x﹣8.
(1)若抛物线的对称轴为y轴,求m的值;
(2)若抛物线的顶点在x正半轴上,求m的值.
18.二次函数图像的顶点坐标是(-2,3),并经过点(1,2),求这个二次函数的函数关系式.
19. 已知二次函数的图象经过,两点,求b,c的值.
20.某商店购进一批单价为20元的日用商品,如果以单价30元销售,那么半月内可售出400件,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件,如果提高售价,请问将售价定每件为多少元时,才能在半月内获得最大利润?并求出最大利润.
21.如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)求抛物线的表达式;
(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;
(3)如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
22.如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=﹣ x2+ x+4经过A、B两点.
(1)写出点A、点B的坐标;
(2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连接PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;
(3)在(2)的条件下,是否存在t,使得△PAM是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
答案解析部分
1.【答案】B
【解析】【解答】解:二次函数y=(x+2)2+3的图象的顶点坐标为(﹣2,3).
故答案为:B.
【分析】根据二次函数的解析式求解即可。
2.【答案】C
【解析】【解答】解:由二次函数 可得: ,
∵ ,
∴当x=1时,二次函数有最大值为-4;
故答案为:C.
【分析】由二次函数 中,a=-1<0,可得抛物线开口向下,函数存在最大值,利用二次函数的性质求出其最大值即可.
3.【答案】A
【解析】【解答】解:∵ ,
∴对称轴为直线x=- ,
故答案为:A.
【分析】抛物线(a≠0)的对称轴为直线x=,据此计算即可.
4.【答案】B
【解析】【解答】解:①因为a=3>0,它们的图象都是开口向上,此说法正确;
② 对称轴是y轴,顶点坐标是(0,1), 的对称轴是x=1,顶点坐标是(1,0),此说法错误;
③二次函数 ,当x>0时,y随着x的增大而增大; 当 时,y随着x的增大而增大;此说法错误;
④因为a=3,所以它们的开口的大小是一样的,此选项正确.
综上所知,正确的有①④两个.
故答案为:B.
【分析】①由两个二次函数的解析式可得a=3>0,于是可得这两个二次函数的图象的开口向上;
②由抛物线y=3x2+1可知其对称轴是y轴,顶点坐标是(0,1);由抛物线y=3(x-1)2可知其对称轴是x=1,顶点坐标是(1,0);
③结合②的结论可知:抛物线y=3x2+1,当x>0时,y随着x的增大而增大;抛物线y=3(x-1)2,当 时,y随着x的增大而增大;
④由两个二次函数的解析式可得a=3,于是可得它们的开口的大小是一样的.
5.【答案】A
【解析】【解答】解:∵抛物线与x轴的交点坐标为(﹣2,0),(0,0),
∴对称轴为x= =﹣1,故①正确;
∵抛物线开口向下,a<0,抛物线与原点相交,c=0,
∴abc=0,故②正确;
∵c=0,
∴b2﹣4a(c+1)=b2﹣4a>0,故③正确;
当x=﹣1时,抛物线有最大值,
∴无论x取何值,ax2+bx+c≤a﹣b+c,
即ax2+bx≤a﹣b,故④正确.
正确的为①②③④,
故答案为:A.
【分析】根据抛物线与x轴两交点的坐标,及抛物线的对称性即可得出其对称轴直线是x=-1,故①正确;抛物线开口向下,a<0,抛物线与原点相交,c=0,抛物线的对称轴在y轴的左侧,故a,b同号,从而得出b<0,故abc=0,故②正确;算出方程 ax2+bx+c+1=0 的根的判别式的值,由判别式的值大于0,得出该方程 有两个不相等的实数根 ,故③正确;当x=﹣1时,抛物线有最大值,故无论x取何值,ax2+bx+c≤a﹣b+c,即ax2+bx≤a﹣b,故④正确,综上所述即可得出答案。
6.【答案】C
【解析】【解答】解:由二次函数 知,二次函数的开口向上,对称轴为直线x=2,
又-2对应的点离对称轴最远,2对应的点离对称轴最近,
∴
故答案为:C.
【分析】根据二次函数的图象开口向上,则离对称轴越远的点的函数值越大即可解答.
7.【答案】D
【解析】【解答】由解析式y=-kx2+k可得:抛物线对称轴x=0;
选项A,由双曲线的两支分别位于二、四象限,可得k<0,则-k>0,抛物线开口方向向上、抛物线与y轴的交点为y轴的负半轴上;本图象与k的取值相矛盾,选项A不符合题意;
选项B,由双曲线的两支分别位于一、三象限,可得k>0,则-k<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象与k的取值相矛盾,选项B不符合题意;
选项C,由双曲线的两支分别位于一、三象限,可得k>0,则-k<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的负半轴上,本图象与k的取值相矛盾,选项C不符合题意;
选项D,由双曲线的两支分别位于一、三象限,可得k>0,则-k<0,抛物线开口方向向上、抛物线与y轴的交点在y轴的负半轴上,本图象与k的取值相矛盾,选项D符合题意.
故答案为:D.
【分析】先由反比例函数的图象得到字母系数的正负,再与二次函数的图象相比较看是否一致,由此即可解答.
8.【答案】D
【解析】【解答】二次函数y=-(x-m)2+m2+1,
可化为:y=-x2+2mx+1,
故二次函数的对称轴为直线x=m,
①m<-2时,x=-2时二次函数有最大值,
此时-(-2-m)2+m2+1=3,
解得m=- ,与m<-2矛盾,故m值不存在;
②当-2≤m≤1时,x=m时,二次函数有最大值,
此时,m2+1=3,
解得m=- ,m= (舍去);
③当m>1时,x=1时二次函数有最大值,
此时,-(1-m)2+m2+1=3,
解得m= .
综上所述,m的值为 或- .
故答案为:D.
【分析】求出二次函数对称轴为直线x=m,再分m<-2,-2≤m≤1,m>1三种情况,根据二次函数的增减性列方程求解即可.
9.【答案】B
【解析】【解答】抛物线y=ax2+2ax的对称轴为直线x=﹣ =﹣1,
∵抛物线y=ax2+2ax在其对称轴的左侧y随x的增大而减小,
∴a>0,抛物线的开口向上,
当y=0时,ax2+2ax=0,解得 ,
即抛物线y=ax2+2ax与x轴的交点坐标为 ,如图所示:
∵关于x的方程ax2+2ax=m(m>0)的一个根为﹣4,
∴关于x的方程ax2+2ax=m(m>0)的另一个根为2,
∵关于x的方程ax2+2ax=n(0<n<m)有两个整数根,
∴关于x的方程ax2+2ax=n(0<n<m)有两个整数根只能为 ,
∴这两个根的积是为﹣3.
故答案为:B.
【分析】 先求得抛物线y=ax2+2ax的对称轴,开口向上,利用抛物线的对称性得到方程ax2+2ax=m的另一个根,利用图象法得到方程ax2+2ax=n的两个整数根,即可求出这两个根的积.
10.【答案】D
【解析】【解答】解:①∵抛物线开口向上,∴a>0,
∵抛物线的对称轴在y轴右侧,∴b<0
∵抛物线与y轴交于负半轴,
∴c<0,
∴abc>0,①不符合题意;
②当x= 1时,y>0,∴a b+c>0,
∵ =1,∴b= 2a,
把b= 2a代入a b+c>0中得3a+c>0,所以②符合题意;
③当x=1时,y<0,∴a+b+c<0,
∴a+c< b,
当x= 1时,y>0,∴a b+c>0,
∴a+c>b,
∴|a+c|<|b|
∴(a+c)2<b2,所以③符合题意;
④∵抛物线的对称轴为直线x=1,
∴x=1时,函数的最小值为a+b+c,
∵ ,∴-m<0,
由图像可知,当x=-m时,y>a+b+c,
∴ ,④符合题意.
⑤令y2= ,则y2≥1,根据函数图像可得交点的横坐标为一正一负,故方程 有一正一负两个实数解,符合题意.
故答案为:D.
【分析】①由抛物线开口方向得到a>0,对称轴在y轴右侧,得到a与b异号,又抛物线与y轴正半轴相交,得到c<0,可得出abc>0,选项①不符合题意;
②把b= 2a代入a b+c>0中得3a+c>0,所以②符合题意;
③由x=1时对应的函数值y<0,可得出a+b+c<0,得到a+c< b,x= 1时,y>0,可得出a b+c>0,得到|a+c|<|b|,即可得到(a+c)2 b2<0,选项③符合题意;
④由对称轴为直线x=1,即x=1时,y有最小值,可得结论,即可得到④符合题意.
⑤令y2= ,则y2≥1,根据函数图像可得交点的横坐标为一正一负,故可判断⑤.
11.【答案】3
【解析】【解答】解:根据二次函数图象过原点,把 代入解析式,
得 ,整理得 ,解得 ,
∵ ,
∴ ,
∴ .
故答案为:3.
【分析】先求出,再求出,最后计算求解即可。
12.【答案】y=(x+2)2+7或y=x2+4x+11
【解析】【解答】解:二次函数y=x2﹣2x+3=(x﹣1)2+2的图象在坐标平面内向左平移3个单位,再向上平移5个单位后图象对应的二次函数解析式为y=(x﹣1+3)2+2+5,即y=(x+2)2+7或y=x2+4x+11.
故答案为:y=(x+2)2+7或y=x2+4x+11(两种形式都可以).
【分析】根据抛物线的平移规律“左加右减、上加下减”可求解.
13.【答案】
【解析】【解答】解:由题意可知:
解得:或.
故答案为: .
【分析】将点 代入 抛物线 得出两个方程,再根据抛物线在x轴上截得的线段长为4,列出第三个方程,然后解这三个方程组成的方程组即可求出a的值.
14.【答案】①④
【解析】【解答】由A(﹣1,0),B(0,﹣2),得b=a﹣2,
∵开口向上,
∴a>0;
∵对称轴在y轴右侧,
∴﹣ >0,
∴﹣ >0,
∴a﹣2<0,
∴a<2;
∴0<a<2;
∴①符合题意;
∵抛物线与y轴交于点B(0,﹣2),
∴c=﹣2,故③不符合题意;
∵抛物线图象与x轴交于点A(﹣1,0),
∴a﹣b﹣2=0,无法得到0<a<2;②﹣1<b<0,故①②不符合题意;
∵|a|=|b|,二次函数y=ax2+bx+c的对称轴在y轴的右侧,
∴二次函数y=ax2+bx+c的对称轴为y= ,
∴x2=2> ﹣1,故④符合题意.
故答案为①④.
【分析】根据抛物线与y轴交于点B(0,-2),可得c=-2,依此判断③;由抛物线图象与x轴交于点A(-1,0),可得a-b-2=0,依此判断①②;由|a|=|b|可得二次函数y=ax2+bx+c的对称轴为x= ,可得x2=2,比较大小即可判断④;从而求解.
15.【答案】209-30
【解析】【解答】解:以AC为y轴,AB为x轴,A为原点建立坐标系,过点D'作D'P⊥x轴交CD于点Q,交x轴于点P,如图所示:
∵ 正中间的球网GH,
∴,
∵点N在离球台正中间的球网GH左侧72cm处到达最高点高出台面21cm,
∴AM=AH-MH=137-72=65,NM=21,
∴设抛物线的解析式为y=a(x-65)2+21,
由旋转得,,
∴在Rt△D'CQ中,CQ=D'Q=5,
∴D'(5,17),
把D'代入y=a(x-65)2+21得,
∴,
当y=0时,,
解得,(不合题意,舍去),
∴,
故答案为:.
【分析】以AC为y轴,AB为x轴,A为原点建立坐标系,过点D'作D'P⊥x轴交CD于点Q,交x轴于点P,易得点N的坐标,再设抛物线的解析式为y=a(x-65)2+21,由旋转的性质结合特殊三角函数的值即可求出点D'的坐标,将D'代入函数解析式即可求出抛物线解析式,进而令y=0,解出x,再由即可求解.
16.【答案】 或 或
【解析】【解答】解:∵顶点 B 的横坐标是1,
解之:b=-4
∴抛物线的解析式为:y=2x2-4x=-2(x-1)2+2,
∴点B(1,2)
设点A(m,2m2-4m),
∴OA2=m2+(2m2-4m)2,OB2=22+1=5,AB2=(m-1)2+(2m2-4m+2)2
当AB2+OB2=OA2时
∴(m-1)2+(2m2-4m+2)2+5=m2+(2m2-4m)2,
整理得:4m2-9m+5=0
解之:m1=,m2=1(舍去),
∴2m2-4m=
∴点A;
当∠OAB=90°时,过点A作AN⊥x轴于点N,过点B作EM⊥y轴于点E,交NA的延长线于点M,
∴∠ONA=∠AMB=90°,
∴∠BAM+∠ABM=90°,∠NAO+∠BAM=90°,
∴∠ABM=∠NAO,
∴△NAO∽△ABM,
∴
设ON=a,NA=c,
∴AM=2-c,BM=a-1,点A(a,-c)
∴-c=2a2-4a,
∴
∴a2-a=2c-c2,
解之:
∴点A();
当OB2+OA2=AB2时,
5+m2+(2m2-4m)2=(m-1)2+(2m2-4m+2)2,
整理得:4m2-9m=0
解之:m1=,m2=0
当m=时,2m2-4m=
∴点A .
∴点A或或.
故答案为:或(或.
【分析】利用顶点的横坐标为1,可求出b的值,即可得到函数解析式,利用函数解析式求出顶点B的坐标;设点A(m,2m2-4m),利用勾股定理分别表示出AB2、OB2、OA2,利用勾股定理分情况讨论:当AB2+OB2=OA2时;当OB2+OA2=AB2时;分别建立关于m的方程,解方程求出符合题意的m的值,即可得到点A的坐标;当∠OAB=90°时,过点A作AN⊥x轴于点N,过点B作EM⊥y轴于点E,交NA的延长线于点M,易证△NAO∽△ABM,利用全等三角形的性质可得对应边成比例,设ON=a,NA=c,可表示出AM,BM的长,同时可得到点A的坐标,将点A的坐标代入函数解析式,可得到关于a,c的方程组,解方程组求出a,c的值,可得点A的坐标;综上所述可得到符合题意的点A的坐标.
17.【答案】(1)解:∵抛物线y=﹣2x2+(m﹣3)x﹣8的对称轴为y轴,
∴﹣ =0,
解得,m=3,即m的值是3;
(2)解:∵抛物线y=﹣2x2+(m﹣3)x﹣8的顶点在x正半轴上,
∴ ,
解得m=11, 即m的值是11.
【解析】【分析】(1)根据对称轴公式 即可求m的值;(2)根据顶点坐标公式求解即可.
18.【答案】解:设二次函数解析式为y=a(x+2)2+3,
把(1,2)代入得9a+3=2,解得a= ,
所以二次函数解析式为:y= (x+2)2+3.
【解析】【分析】利用顶点式,利用待定系数法求解二次函数解析式即可。
19.【答案】解:把A(0,3) ,B(-4,-) 分别代入,
得,
解得.
故,c=3.
【解析】【分析】将点A、B的坐标代入求解就可得到b、c的值.
20.【答案】解:设售价定每件为 元,利润为 元,依题意可得
,
整理得 ,
配方得 ,
∵-20<0,
∴当 时, 的最大值为4500元.
答:售价定为每件35元时,才能在半月内获得最大利润,最大利润为4500元.
【解析】【分析】 设售价定每件为 元,利润为 元,根据“利润=单件利润×销售量”求得函数关系式,然后利用二次函数的性质求最大值即可.
21.【答案】(1)将点A(-1,0),B(4,0)的坐标代入函数的表达式得:
,
解得:b=3,c=4.
抛物线的解析式为y=-x2+3x+4.
(2)如图1所示: ∵令x=0得y=4, ∴OC=4.
∴OC=OB.
∵∠CFP=∠COB=90°, ∴FC=PF时,以P,C,F为顶点的三角形与△OBC相似.
设点P的坐标为(a,-a2+3a+4)(a>0).
则CF=a,PF=|-a2+3a+4-4|=|a2-3a|.
∴|a2-3a|=a.
解得:a=2,a=4.
∴点P的坐标为(2,6)或(4,0).
(3)如图2所示:连接EC. 设点P的坐标为(a,-a2+3a+4).则OE=a,PE=-a2+3a+4,EB=4-a.
∵S四边形PCEB= OB PE= ×4(-a2+3a+4),S△CEB= EB OC= ×4×(4-a),
∴S△PBC=S四边形PCEB-S△CEB=2(-a2+3a+4)-2(4-a)=-2a2+8a.
∵a=-2<0,
∴当a=2时,△PBC的面积S有最大值.
∴P(2,6),△PBC的面积的最大值为8.
【解析】【分析】(1)抛物线过AB两点,将两点坐标代入即可求出bc 的值,从而得到抛物线表达式。
(2)已知抛物线函数表达式,即可求出与y轴交点点C的坐标。得OC=OB。△COB是等腰三角形。若要△CPF∽△CBO,故△CPF是等腰三角形。即CF=PF。从而求出点P的坐标。
(3) 设点P的坐标为(a,-a2+3a+4) ,将各边表示出来。然后分别写出四边形PCEB的面积公式以及三角形CEB的面积公式,即可将三角形PBC的面积表示出来。即可求出a 的取值。
22.【答案】(1)解:抛物线y=﹣0.5x2+3.5x+4中:令x=0,y=4,则 B(0,4);
令y=0,0=﹣0.5x2+3.5x+4,解得 x1=﹣1、x2=8,则 A(8,0);∴A(8,0)、B(0,4).
(2)解:△ABC中,AB=AC,AO⊥BC,则OB=OC=4,∴C(0,﹣4).
由A(8,0)、B(0,4),得:直线AB:y=﹣0.5x+4;
依题意,知:OE=2t,即 E(2t,0);
∴P(2t,﹣2t2+7t+4)、Q(2t,﹣t+4),PQ=(﹣2t2+7t+4)﹣(﹣t+4)=﹣2t2+8t;
S=S△ABC+S△PAB=0.5×8×8+0.5×(﹣2t2+8t)×8=﹣8t2+32t+32=﹣8(t﹣2)2+64;
∴当t=2时,S有最大值,且最大值为64.
(3)解:∵PM∥y轴,∴∠AMP=∠ACO<90°;
而∠APM是锐角,所以△PAM若是直角三角形,只能是∠PAM=90°;
由A(8,0)、C(0,﹣4),得:直线AC:y=0.5x﹣4;
所以,直线AP可设为:y=﹣2x+h,代入A(8,0),得:﹣16+h=0,h=16
∴直线AP:y=﹣2x+16,联立抛物线的解析式,∴存在符合条件的点P,且坐标为(3,10).
【解析】【分析】(1)抛物线的解析式中,令x=0,能确定点B的坐标;令y=0,能确定点A的坐标.(2)四边形PBCA可看作△ABC、△PBA两部分;△ABC的面积是定值,关键是求出△PBA的面积表达式;若设直线l与直线AB的交点为Q,先用t表示出线段PQ的长,而△PAB的面积可由( PQ OA)求得,在求出S、t的函数关系式后,由函数的性质可求得S的最大值.(3)△PAM中,∠APM是锐角,而PM∥y轴,∠AMP=∠ACO也不可能是直角,所以只有∠PAC是直角一种可能,即 直线AP、直线AC垂直,此时两直线的斜率乘积为-1,先求出直线AC的解析式,联立抛物线的解析式后可求得点P的坐标
