2021-2022学年北师大版九年级数学下册第2章二次函数单元综合达标测试(word解析版)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册第2章二次函数单元综合达标测试(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 15:13:45 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学下册《第2章二次函数》单元综合达标测试(附答案)
一、单选题(满分40分)
1.下列函数中,不是二次函数的是( )
A.y=2x2+2x B.
C.y=x2﹣2x+1 D.y=x2﹣x(2+x).
2.设是抛物线上的三点,则的大小关系为( )
A. B. C. D.
3.抛物线y=(x﹣2)2+1的顶点坐标为( )
A.(2,1) B.(2,﹣1) C.(﹣2,﹣1) D.(﹣2,1)
4.把抛物线向上平移1个单位,再向右平移3个单位,得到的抛物线是( )
A. B.
C. D.+2
5.二次函数y=x2+bx+3满足当x<﹣2时,y随x的增大而减小,当x>﹣2时,y随x的增大而增大,则x=1时,y的值等于( )
A.﹣8 B.0 C.3 D.8
6.已知抛物线y=x2﹣2x﹣1与x轴的一个交点为(m,0),则代数式m2﹣2m+2021的值为( )
A.2020 B.2021 C.2022 D.2023
7.二次函数()的图象如图所示,反比例函数与正比例函数在同一坐标系内的大致图象是( )
A. B. C. D.
8.已知:抛物线的对称轴为直线,与轴的一个交点坐标为,其部分图如图所示,下列结论:①;②方程的两个根是,;③;④当时,的取值范围是;⑤当时,随增大而增大
其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(满分40分)
9.抛物线y=ax2+bx+c的对称轴为x=1,点P,点Q是抛物线与x轴的两个交点,若点P的坐标为(3,0),则点Q的坐标为______.
10.二次函数y=﹣2x2+1的图象上有两点A(x1,y1)、B(x2,y2),且x1≠x2,y1=y2,当x=x1+x2时,对应的函数值y=___.
11.如图,在平面直角坐标系中,抛物线与交于点A.过点A作y轴的垂线,分别交两条抛物线于点B、C(点B在点A的左侧,点C在点A的右侧).线段BC的长为________________.
12.如图,某运动员推铅球,铅球行进高度与水平距离之间的关系是,则此运动员将铅球推出的距离是________m.
13.如图,在平面直角坐标系xOy中,等腰△ABO的顶点A在y轴上,AB=OB,tan∠AOB=2,抛物线y=﹣x2+bx+2过点A.
(1)若点O关于AB中点的中心对称点也恰好在抛物线y=﹣x2+bx+2上,则b=________;
(2)若将△ABO绕点A按逆时针方向旋转45°,得到,点在抛物线y=﹣x2+bx+2上,则b=________.
14.正方形ABCD的边长为1, E为边BC上动点,将AE绕点E顺时针旋转90°得到线段EF,M为DE的中点,连接MF,则MF的最小值为________
15.已知二次函数(a>0)的图象与x轴正半轴交于A(p,0)和B(q,0)两点(点A在点B的左边),方程(a>0)的解为x=m或x=n(m<n),则p,q,m,n的大小关系可能是_____(用“<”号连接)
16.某电商平台11月1日起开始销售一款新品牌手机,当月的日销售额y(万元)和销售时间第x天(1≤x≤30且x为整数)之间满足二次函数关系y=-(x-h)+k,根据市场调查可以确定在当月中旬日销售额达到最大值.
(1)若第18天的销售额比第19天的销售额多5万元,则第__________天的日销售额最大;
(2)若第18天后的日销售额呈下降趋势,则h的取值范围是___________
三、解答题(满分40分)
17.已知二次函数的图象经过,两点.
(1)求这个二次函数的表达式.
(2)是否存在点在这个函数图象上,若存在,请求出m的值;若不存在,请说明理由.
18.中国小将杨倩在2021东京奥运会射击比赛中,拿下中国第一枚金牌.某网店顺势推出纪念T恤衫,成本为30元/件,经市场调查发现每天销售量y(件)与销售单价x(元)之间存在一次函数关系,如图所示.
(1)直接写出y与x之间的函数关系式.
(2)当销售单价为多少时,每天获得的利润最大?最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出160元给希望工程,为了保证捐款后每天利润不低于3800元,求该纪念T恤衫的销售单价x的取值范围.
19.如图,抛物线y=ax2+bx+c与x轴交于A(﹣2,0)、B(6,0)两点,与y轴交于点C.直线l与抛物线交于A、D两点,与y轴交于点E,点D的坐标为(4,3).
(1)求抛物线的解析式与直线l的解析式;
(2)若点P是抛物线上的点且在直线l上方,连接PA、PD,求当△PAD面积最大时点P的坐标及该面积的最大值;
(3)若点Q是y轴上的点,且∠ADQ=45°,求点Q的坐标.
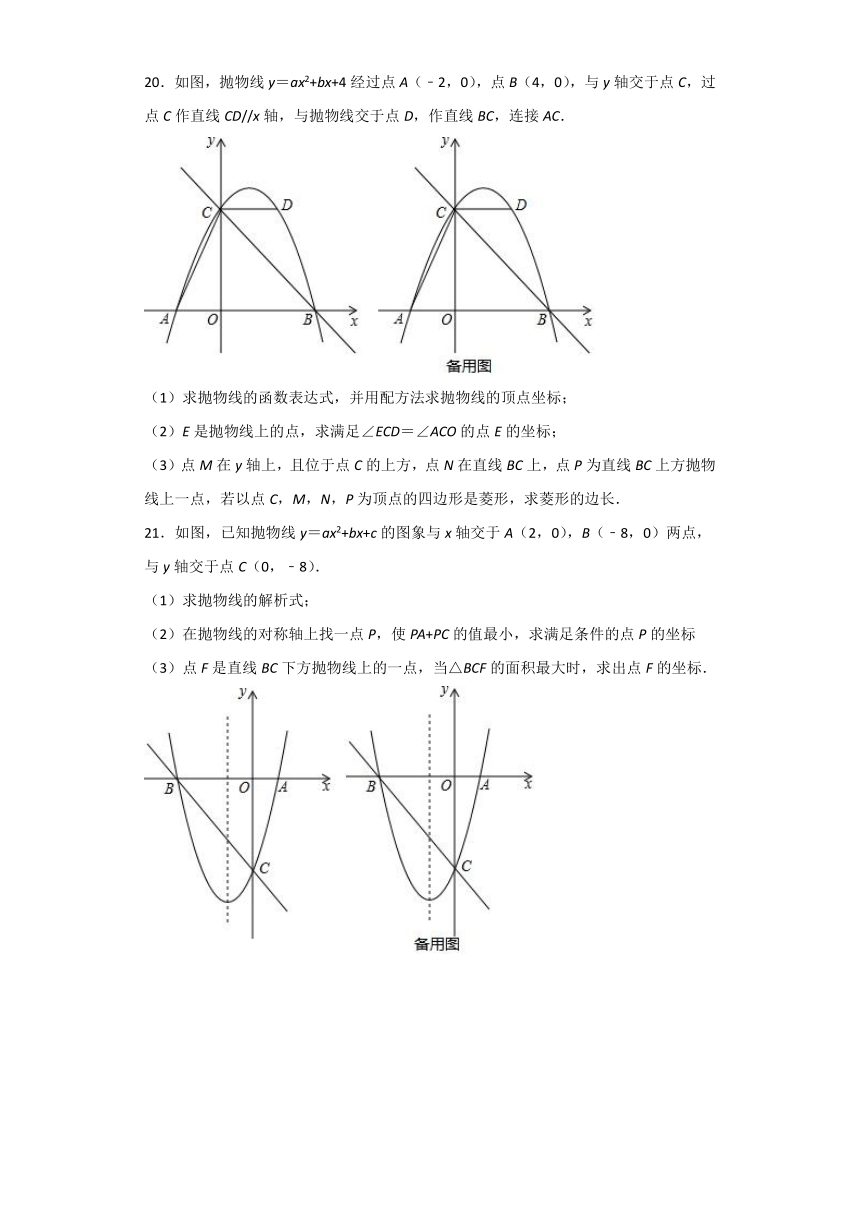
20.如图,抛物线y=ax2+bx+4经过点A(﹣2,0),点B(4,0),与y轴交于点C,过点C作直线CD//x轴,与抛物线交于点D,作直线BC,连接AC.
(1)求抛物线的函数表达式,并用配方法求抛物线的顶点坐标;
(2)E是抛物线上的点,求满足∠ECD=∠ACO的点E的坐标;
(3)点M在y轴上,且位于点C的上方,点N在直线BC上,点P为直线BC上方抛物线上一点,若以点C,M,N,P为顶点的四边形是菱形,求菱形的边长.
21.如图,已知抛物线y=ax2+bx+c的图象与x轴交于A(2,0),B(﹣8,0)两点,与y轴交于点C(0,﹣8).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上找一点P,使PA+PC的值最小,求满足条件的点P的坐标
(3)点F是直线BC下方抛物线上的一点,当△BCF的面积最大时,求出点F的坐标.
参考答案
1.D
解:根据二次函数的定义知,A、B、C三个选项中的函数均是二次函数,而选项D的函数化简后是一次函数y=-2x.
故选:D
2.A
解:∵当x= 2时,y= (x+1)2+k= 1+k;当x=1时,y= (x+1)2+k= 4+k;当x=2时,y= (x+1)2+k= 9+k;
∵ 1+k> 4+k> 9+k
∴.
故选:A.
3.A
解:抛物线y=(x﹣2)2+1是以抛物线的顶点式给出的,
其顶点坐标为:(2,1).
故选:A.
4.C
解:将抛物线向上平移1个单位,再向右平移3个单位,得到的抛物线是,即;
故选:C.
5.D
解:∵二次函数y=x2+bx+3,当x<﹣2时,y随x的增大而减小;当x>﹣2时,y随x的增大而增大,
∴对称轴为x=﹣2,
∴﹣=﹣2,
∴b=4,
∴二次函数y=x2+4x+3,
当x=1时,y=1+4+3=8.
故选:D.
6.C
解: 抛物线y=x2﹣2x﹣1与x轴的一个交点为(m,0),
故选C
7.B
解:抛物线的开口向上,与轴的交点位于轴的正半轴,
,
抛物线的对称轴位于轴的右侧,
,
,
,
由可知,反比例函数的图象位于第二、四象限,
由可知,正比例函数的图象经过原点,且经过第一、三象限,
故选:B.
8.B
解:①∵抛物线与x轴有2个交点,
∴b2﹣4ac>0,即4ac<b2,所以①正确;
②∵抛物线的对称轴为直线x=1,
而点(﹣1,0)关于直线x=1的对称点的坐标为(3,0),
∴方程ax2+bx+c=0的两个根是x1=﹣1,x2=3,所以②正确;
③∵抛物线y=ax2+bx+c(a≠0)经过点(﹣1,0),
∴a﹣b+c=0,所以③错误;
④∵抛物线与x轴的两点坐标为(﹣1,0),(3,0),
∴当﹣1<x<3时,y>0,所以④错误;
⑤∵抛物线的对称轴为直线x=1,
∴当x<1时,y随x增大而增大,所以⑤正确.
故选:B.
9.(-1,0)
解:∵抛物线的对称轴为直线x=1,点P的坐标为(3,0),
∴点Q的横坐标为1×2-3=-1,
∴点Q的坐标为(-1,0).
故答案为:(-1,0).
10.1
解:∵二次函数y=﹣2x2+1的对称轴是y轴(即直线x=0),函数的图象关于y轴对称,
∵二次函数y=﹣2x2+1的图象上有两点A(x1,y1)、B(x2,y2),且x1≠x2,y1=y2,
∴x1=﹣x2,即x1+x2=0,
当x=x1+x2=0时,y=﹣2×02+1=1,
故答案为:1.
11.10
解:设抛物线y=a(x+2)2+b-1的对称轴与线段BC交于点E,抛物线y=a(x﹣3)2+b的对称轴与线段BC交于点F,如图所示.
由抛物线的对称性,可知:BE=AE,CF=AF,
∵抛物线y=a(x+2)2+b-1的对称轴为直线x=﹣2,抛物线y=a(x﹣3)2+b的对称轴为直线x=3,
∴BC=BE+AE+AF+CF=2(AE+AF)=2×[3﹣(﹣2)]=10.
故答案为:10.
12.12
解:∵,
∴当y=0时,,
解得x1=12,x2=-2(舍去),
∴此运动员将铅球推出的距离是12m.
故答案为:12.
13.
解:(1)如图1,过点B作BC⊥x轴于C,
当x=0时,y=2,
∴A(0,2)
∵AB=0B,
∴
∵
∴BC=2
∴B(2,1)
∵AB的中点坐标为(1,),
∴点O关于AB中点的中心对称点的坐标为(2,3),
∵该点也恰好在抛物线y=-x2+bx+2上,
∴-4+2b+2=3,解得b=;
故答填;
(2)如图2,过点B'作B'H⊥AB于H,过H作GM⊥y轴于G,过点B'作B'M⊥GM于M,
由(1)得:AB=,
由旋转的性质可得:AB'=AB=,∠BAB'=45°,
∵∠AHB'=90°,
∴△AHB'是等腰直角三角形,
∴
∵∠AGH=∠GAH+∠AHG=∠AHG+∠MHB'=90°,
∴∠GAH=∠MHB',
∵∠AGH=∠M=90°,AH=B'H,
∴△AGH≌△HMB'{AAS),
∴GH=B'M,HM=AG,
∵,
∴AG=HM=,GH=B'M=,
∴
∴
∵该点也恰好在抛物线y=-x2+bx+2上,
∴,解得b=.
故答填.
14.
解:方法一:连接AC,AF,CF,A点是定点,E,F动点,
∵AE=EF,AE⊥EF,
∴∠EAF=45°, ,
在正方形ABCD中,∠BAC=45°, ,
∵∠BAE=∠BAC-∠EAC, ∠CAF=∠EAF-∠EAC,
∴∠BAE=∠CAF,
又∵ ,
∴△ABE∽△ACF,
∴∠ACF=∠ABE=90°,
∴∠DCF=45°,
∴F在射线CF上运动,且∠DCF=45°.
取EC的中点H,连接MH,
∵MD=ME,
∴,,
∴MH⊥EC,
过F点作FP⊥MH,
∴四边形FGHP是矩形,
∴PH=FG
设,则, ,
∴,
,
在Rt△MPF中, ,
即:,
∴,
当时,的最大值为,
∴的最大值为,
故答案为.
方法二:解:如图,过点F作FG⊥BC垂足为G,
∵在正方形ABCD中,AB=BC=CD=1,∠ABC=90°,
由旋转性质可知:AE=FE,∠AEF=90°,
∴,
∴,
∴(SAS) ,
∴,,
∵,
∴,
∴,
取EC的中点H,连接MH,
∵MD=ME,
∴,,
∴MH⊥EC,
过F点作FP⊥MH,
∴四边形FGHP是矩形,
∴PH=FG
设,则, ,
∴,
,
在Rt△MPF中, ,
即:,
∴,
当时,的最小值为,
∴的最大值为,
故答案为.
方法三:以点B为原点,BC所在直线为x轴,建立平面直角坐标系,
设点E(a,0),
∵正方形的边长为1,
∴点D(1,1);
过点F作FG⊥x轴,垂足为G,
∵∠AEF=90°,
∴∠BAE=∠GEF,
∵∠ABE=∠EGF=90°,AE=EF,
∴△ABE≌△EGF,
∴BE=GF,AB=EG=1,
∴M(,),F(,a),
∴MF=
=
=
=
=,
当a=时,MF有最小值,且最小值为;
故答案为:.
15.
解:依据题意的大致图象如下图所示,
在此基础上,作出直线的图象,设两个函数图象的交点为、,
则、的横坐标为,,
∴由图象可得:,
故答案为.
16.16 9<x<
解:(1)根据第18天的销售额比第19天的销售额多5万元,
则:,
解得:,
∴第天的销售额最大,
故答案为:;
(2)∵y=-(x-h)+k,
则,随增大而增大,
,随增大而减小,且为整数,
则,解得,
∵当月中旬日销售额达到最大值,
则,
综上:.
17.(1);(2)存在;或.
解:(1)∵二次函数的图象经过,两点.
∴,
解得:,
∴这个二次函数的表达式;
(2)根据题意,
令,则,
∴,
解得:或,
∴或.
18.(1);(2)当销售单价为50元时,每天获得的利润最大,最大值为4000元;(3)
解:(1)设y与x之间的函数关系式为;
将代入得:
解得
y与x之间的函数关系式为
(2)设利润为,则,
即
,开口向下
当时,
当销售单价为50元时,每天获得的利润最大,最大值为4000元
(3)根据题意可得
即
当,解得
,开口向下
由(2)可知,当时取得最大值,
19.(1)yx2+x+3;yx+1;(2)△PAD的面积的最大值为,P(1,);(3)点Q的坐标为(0,)或(0,﹣9)
解:(1)∵抛物线y=ax2+bx+c与x轴交于A(﹣2,0)、B(6,0)两点,
∴设抛物线的解析式为y=a(x+2)(x﹣6),
∵D(4,3)在抛物线上,
∴3=a(4+2)×(4﹣6),解得a,
∴抛物线的解析式为y(x+2)(x﹣6)x2+x+3,
∵直线l经过A(﹣2,0)、D(4,3),
设直线l的解析式为y=kx+m(k≠0),
则,解得,,
∴直线l的解析式为yx+1;
(2)如图1中,过点P作轴交AD于点T.
设P(m, m2+m+3),则T(m,m+1).
∵S△PAD (xD﹣xA) PT=3PT,
∴PT的值最大值时,△PAD的面积最大,
∵PTm2+m+3m﹣1m2m+2(m﹣1)2,
∵0,抛物线开口向下,
∴m=1时,PT的值最大,最大值为,
此时△PAD的面积的最大值为,P(1,).
(3)如图2中,将线段AD绕点A逆时针旋转90°得到AT,
过作轴于 过作轴于
T(﹣5,6),
设DT交y轴于点Q,则∠ADQ=45°,
∵D(4,3),∴直线DT的解析式为yx,
∴Q(0,),作点T关于AD的对称点,
同理可得(1,﹣6),
则直线DT′的解析式为y=3x﹣9,
设DQ′交y轴于点Q′,则∠ADQ′=45°,
∴Q′(0,﹣9),
综上所述,满足条件的点Q的坐标为(0,)或(0,﹣9).
20.(1)yx2+x+4;顶点坐标为(1,);(2)点E的坐标为(3,);或(1,);(3)菱形的边长为
解:(1)∵抛物线的图象经过点A(﹣2,0),点B(4,0),
∴,
∴解得,
∴抛物线解析式为,
∵,
∴抛物线的顶点坐标为(1,);
(2)如图1,
①当点E位于直线CD下方时,过点E作EF⊥CD,垂足为F,设满足条件的点在抛物线上:
则,,,
根据题意,当时,,
即,
∴,
解得(舍去),,
∴;
②当点E'位于直线CD上方时,过点E'作E'F'⊥直线CD,垂足为F',设
则,,,
根据题意,当时,,
即,
∴,
解得(舍去),,
∴,
所以,点E的坐标为或;
(3)①CM为菱形的边,如图2,
在第一象限内取点P′,过点P′作轴,交BC于N′,过点P′作,交y轴于M′,
∴四边形CM′P′N′是平行四边形,
∵四边形CM′P′N′是菱形,
∴,
过点P′作轴,垂足为Q′,
∵,,
∴,
∴,设点,
在中,,,
∵,,
∴直线BC的解析式为,
∵轴,
∴,
∴,
∴,
解得:(舍)或,
菱形CM′P′N′的边长为;
②CM为菱形的对角线,如图3,
在第一象限内抛物线上取点P,过点P作,交y轴于点M,连接CP,过点M作,交BC于N,
∴四边形CPMN是平行四边形,连接PN交CM于点Q,
∵四边形CPMN是菱形,
∴,,
∵,
∴,
∴,
∴,
∴,
设点,
∴,,
∴
∴(舍),
∴此种情况不存在.
综上,菱形的边长为.
平行四边形及菱形的性质等,理解题意,作出相应图形结合这些知识点是解题关键.
21.(1);(2)P点坐标为(-3,-5);(3)F的坐标为(-4,-12).
解:(1)∵抛物线y=ax2+bx+c的图象与x轴交于A(2,0),B(﹣8,0)两点,
∴可设抛物线解析式为,
又∵抛物线的图像经过点C(0,-8),
∴,
∴,
∴抛物线解析式为;
(2)如图所示,连接BP,AP,CP,设BC于抛物线对称轴交于 ,
∵A(2,0)、B(-8,0)分别是抛物线与x轴的两个交点,
∴A、B关于抛物线对称轴对称,即关于直线对称,
∴PA=PB,
∴PA+PC=PB+PC,
∴要使PA+PC最小,即PB+PC最小,
∴当B、P、C三点共线时,PB+PC最小,即此时P点在的位置,
设直线BC的解析式为,
∴,
∴,
∴直线BC的解析式为,
当时,,
∴P点坐标为(-3,-5);
(3)如图所示,过点F作FN∥y轴,交BC于N,
设F的坐标为(t,),则N点坐标为(t,-t-8),
∴,
∴
,
∴当时,△BCF的面积最大,
∴F的坐标为(-4,-12).
试卷第1页,共3页
一、单选题(满分40分)
1.下列函数中,不是二次函数的是( )
A.y=2x2+2x B.
C.y=x2﹣2x+1 D.y=x2﹣x(2+x).
2.设是抛物线上的三点,则的大小关系为( )
A. B. C. D.
3.抛物线y=(x﹣2)2+1的顶点坐标为( )
A.(2,1) B.(2,﹣1) C.(﹣2,﹣1) D.(﹣2,1)
4.把抛物线向上平移1个单位,再向右平移3个单位,得到的抛物线是( )
A. B.
C. D.+2
5.二次函数y=x2+bx+3满足当x<﹣2时,y随x的增大而减小,当x>﹣2时,y随x的增大而增大,则x=1时,y的值等于( )
A.﹣8 B.0 C.3 D.8
6.已知抛物线y=x2﹣2x﹣1与x轴的一个交点为(m,0),则代数式m2﹣2m+2021的值为( )
A.2020 B.2021 C.2022 D.2023
7.二次函数()的图象如图所示,反比例函数与正比例函数在同一坐标系内的大致图象是( )
A. B. C. D.
8.已知:抛物线的对称轴为直线,与轴的一个交点坐标为,其部分图如图所示,下列结论:①;②方程的两个根是,;③;④当时,的取值范围是;⑤当时,随增大而增大
其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(满分40分)
9.抛物线y=ax2+bx+c的对称轴为x=1,点P,点Q是抛物线与x轴的两个交点,若点P的坐标为(3,0),则点Q的坐标为______.
10.二次函数y=﹣2x2+1的图象上有两点A(x1,y1)、B(x2,y2),且x1≠x2,y1=y2,当x=x1+x2时,对应的函数值y=___.
11.如图,在平面直角坐标系中,抛物线与交于点A.过点A作y轴的垂线,分别交两条抛物线于点B、C(点B在点A的左侧,点C在点A的右侧).线段BC的长为________________.
12.如图,某运动员推铅球,铅球行进高度与水平距离之间的关系是,则此运动员将铅球推出的距离是________m.
13.如图,在平面直角坐标系xOy中,等腰△ABO的顶点A在y轴上,AB=OB,tan∠AOB=2,抛物线y=﹣x2+bx+2过点A.
(1)若点O关于AB中点的中心对称点也恰好在抛物线y=﹣x2+bx+2上,则b=________;
(2)若将△ABO绕点A按逆时针方向旋转45°,得到,点在抛物线y=﹣x2+bx+2上,则b=________.
14.正方形ABCD的边长为1, E为边BC上动点,将AE绕点E顺时针旋转90°得到线段EF,M为DE的中点,连接MF,则MF的最小值为________
15.已知二次函数(a>0)的图象与x轴正半轴交于A(p,0)和B(q,0)两点(点A在点B的左边),方程(a>0)的解为x=m或x=n(m<n),则p,q,m,n的大小关系可能是_____(用“<”号连接)
16.某电商平台11月1日起开始销售一款新品牌手机,当月的日销售额y(万元)和销售时间第x天(1≤x≤30且x为整数)之间满足二次函数关系y=-(x-h)+k,根据市场调查可以确定在当月中旬日销售额达到最大值.
(1)若第18天的销售额比第19天的销售额多5万元,则第__________天的日销售额最大;
(2)若第18天后的日销售额呈下降趋势,则h的取值范围是___________
三、解答题(满分40分)
17.已知二次函数的图象经过,两点.
(1)求这个二次函数的表达式.
(2)是否存在点在这个函数图象上,若存在,请求出m的值;若不存在,请说明理由.
18.中国小将杨倩在2021东京奥运会射击比赛中,拿下中国第一枚金牌.某网店顺势推出纪念T恤衫,成本为30元/件,经市场调查发现每天销售量y(件)与销售单价x(元)之间存在一次函数关系,如图所示.
(1)直接写出y与x之间的函数关系式.
(2)当销售单价为多少时,每天获得的利润最大?最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出160元给希望工程,为了保证捐款后每天利润不低于3800元,求该纪念T恤衫的销售单价x的取值范围.
19.如图,抛物线y=ax2+bx+c与x轴交于A(﹣2,0)、B(6,0)两点,与y轴交于点C.直线l与抛物线交于A、D两点,与y轴交于点E,点D的坐标为(4,3).
(1)求抛物线的解析式与直线l的解析式;
(2)若点P是抛物线上的点且在直线l上方,连接PA、PD,求当△PAD面积最大时点P的坐标及该面积的最大值;
(3)若点Q是y轴上的点,且∠ADQ=45°,求点Q的坐标.
20.如图,抛物线y=ax2+bx+4经过点A(﹣2,0),点B(4,0),与y轴交于点C,过点C作直线CD//x轴,与抛物线交于点D,作直线BC,连接AC.
(1)求抛物线的函数表达式,并用配方法求抛物线的顶点坐标;
(2)E是抛物线上的点,求满足∠ECD=∠ACO的点E的坐标;
(3)点M在y轴上,且位于点C的上方,点N在直线BC上,点P为直线BC上方抛物线上一点,若以点C,M,N,P为顶点的四边形是菱形,求菱形的边长.
21.如图,已知抛物线y=ax2+bx+c的图象与x轴交于A(2,0),B(﹣8,0)两点,与y轴交于点C(0,﹣8).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上找一点P,使PA+PC的值最小,求满足条件的点P的坐标
(3)点F是直线BC下方抛物线上的一点,当△BCF的面积最大时,求出点F的坐标.
参考答案
1.D
解:根据二次函数的定义知,A、B、C三个选项中的函数均是二次函数,而选项D的函数化简后是一次函数y=-2x.
故选:D
2.A
解:∵当x= 2时,y= (x+1)2+k= 1+k;当x=1时,y= (x+1)2+k= 4+k;当x=2时,y= (x+1)2+k= 9+k;
∵ 1+k> 4+k> 9+k
∴.
故选:A.
3.A
解:抛物线y=(x﹣2)2+1是以抛物线的顶点式给出的,
其顶点坐标为:(2,1).
故选:A.
4.C
解:将抛物线向上平移1个单位,再向右平移3个单位,得到的抛物线是,即;
故选:C.
5.D
解:∵二次函数y=x2+bx+3,当x<﹣2时,y随x的增大而减小;当x>﹣2时,y随x的增大而增大,
∴对称轴为x=﹣2,
∴﹣=﹣2,
∴b=4,
∴二次函数y=x2+4x+3,
当x=1时,y=1+4+3=8.
故选:D.
6.C
解: 抛物线y=x2﹣2x﹣1与x轴的一个交点为(m,0),
故选C
7.B
解:抛物线的开口向上,与轴的交点位于轴的正半轴,
,
抛物线的对称轴位于轴的右侧,
,
,
,
由可知,反比例函数的图象位于第二、四象限,
由可知,正比例函数的图象经过原点,且经过第一、三象限,
故选:B.
8.B
解:①∵抛物线与x轴有2个交点,
∴b2﹣4ac>0,即4ac<b2,所以①正确;
②∵抛物线的对称轴为直线x=1,
而点(﹣1,0)关于直线x=1的对称点的坐标为(3,0),
∴方程ax2+bx+c=0的两个根是x1=﹣1,x2=3,所以②正确;
③∵抛物线y=ax2+bx+c(a≠0)经过点(﹣1,0),
∴a﹣b+c=0,所以③错误;
④∵抛物线与x轴的两点坐标为(﹣1,0),(3,0),
∴当﹣1<x<3时,y>0,所以④错误;
⑤∵抛物线的对称轴为直线x=1,
∴当x<1时,y随x增大而增大,所以⑤正确.
故选:B.
9.(-1,0)
解:∵抛物线的对称轴为直线x=1,点P的坐标为(3,0),
∴点Q的横坐标为1×2-3=-1,
∴点Q的坐标为(-1,0).
故答案为:(-1,0).
10.1
解:∵二次函数y=﹣2x2+1的对称轴是y轴(即直线x=0),函数的图象关于y轴对称,
∵二次函数y=﹣2x2+1的图象上有两点A(x1,y1)、B(x2,y2),且x1≠x2,y1=y2,
∴x1=﹣x2,即x1+x2=0,
当x=x1+x2=0时,y=﹣2×02+1=1,
故答案为:1.
11.10
解:设抛物线y=a(x+2)2+b-1的对称轴与线段BC交于点E,抛物线y=a(x﹣3)2+b的对称轴与线段BC交于点F,如图所示.
由抛物线的对称性,可知:BE=AE,CF=AF,
∵抛物线y=a(x+2)2+b-1的对称轴为直线x=﹣2,抛物线y=a(x﹣3)2+b的对称轴为直线x=3,
∴BC=BE+AE+AF+CF=2(AE+AF)=2×[3﹣(﹣2)]=10.
故答案为:10.
12.12
解:∵,
∴当y=0时,,
解得x1=12,x2=-2(舍去),
∴此运动员将铅球推出的距离是12m.
故答案为:12.
13.
解:(1)如图1,过点B作BC⊥x轴于C,
当x=0时,y=2,
∴A(0,2)
∵AB=0B,
∴
∵
∴BC=2
∴B(2,1)
∵AB的中点坐标为(1,),
∴点O关于AB中点的中心对称点的坐标为(2,3),
∵该点也恰好在抛物线y=-x2+bx+2上,
∴-4+2b+2=3,解得b=;
故答填;
(2)如图2,过点B'作B'H⊥AB于H,过H作GM⊥y轴于G,过点B'作B'M⊥GM于M,
由(1)得:AB=,
由旋转的性质可得:AB'=AB=,∠BAB'=45°,
∵∠AHB'=90°,
∴△AHB'是等腰直角三角形,
∴
∵∠AGH=∠GAH+∠AHG=∠AHG+∠MHB'=90°,
∴∠GAH=∠MHB',
∵∠AGH=∠M=90°,AH=B'H,
∴△AGH≌△HMB'{AAS),
∴GH=B'M,HM=AG,
∵,
∴AG=HM=,GH=B'M=,
∴
∴
∵该点也恰好在抛物线y=-x2+bx+2上,
∴,解得b=.
故答填.
14.
解:方法一:连接AC,AF,CF,A点是定点,E,F动点,
∵AE=EF,AE⊥EF,
∴∠EAF=45°, ,
在正方形ABCD中,∠BAC=45°, ,
∵∠BAE=∠BAC-∠EAC, ∠CAF=∠EAF-∠EAC,
∴∠BAE=∠CAF,
又∵ ,
∴△ABE∽△ACF,
∴∠ACF=∠ABE=90°,
∴∠DCF=45°,
∴F在射线CF上运动,且∠DCF=45°.
取EC的中点H,连接MH,
∵MD=ME,
∴,,
∴MH⊥EC,
过F点作FP⊥MH,
∴四边形FGHP是矩形,
∴PH=FG
设,则, ,
∴,
,
在Rt△MPF中, ,
即:,
∴,
当时,的最大值为,
∴的最大值为,
故答案为.
方法二:解:如图,过点F作FG⊥BC垂足为G,
∵在正方形ABCD中,AB=BC=CD=1,∠ABC=90°,
由旋转性质可知:AE=FE,∠AEF=90°,
∴,
∴,
∴(SAS) ,
∴,,
∵,
∴,
∴,
取EC的中点H,连接MH,
∵MD=ME,
∴,,
∴MH⊥EC,
过F点作FP⊥MH,
∴四边形FGHP是矩形,
∴PH=FG
设,则, ,
∴,
,
在Rt△MPF中, ,
即:,
∴,
当时,的最小值为,
∴的最大值为,
故答案为.
方法三:以点B为原点,BC所在直线为x轴,建立平面直角坐标系,
设点E(a,0),
∵正方形的边长为1,
∴点D(1,1);
过点F作FG⊥x轴,垂足为G,
∵∠AEF=90°,
∴∠BAE=∠GEF,
∵∠ABE=∠EGF=90°,AE=EF,
∴△ABE≌△EGF,
∴BE=GF,AB=EG=1,
∴M(,),F(,a),
∴MF=
=
=
=
=,
当a=时,MF有最小值,且最小值为;
故答案为:.
15.
解:依据题意的大致图象如下图所示,
在此基础上,作出直线的图象,设两个函数图象的交点为、,
则、的横坐标为,,
∴由图象可得:,
故答案为.
16.16 9<x<
解:(1)根据第18天的销售额比第19天的销售额多5万元,
则:,
解得:,
∴第天的销售额最大,
故答案为:;
(2)∵y=-(x-h)+k,
则,随增大而增大,
,随增大而减小,且为整数,
则,解得,
∵当月中旬日销售额达到最大值,
则,
综上:.
17.(1);(2)存在;或.
解:(1)∵二次函数的图象经过,两点.
∴,
解得:,
∴这个二次函数的表达式;
(2)根据题意,
令,则,
∴,
解得:或,
∴或.
18.(1);(2)当销售单价为50元时,每天获得的利润最大,最大值为4000元;(3)
解:(1)设y与x之间的函数关系式为;
将代入得:
解得
y与x之间的函数关系式为
(2)设利润为,则,
即
,开口向下
当时,
当销售单价为50元时,每天获得的利润最大,最大值为4000元
(3)根据题意可得
即
当,解得
,开口向下
由(2)可知,当时取得最大值,
19.(1)yx2+x+3;yx+1;(2)△PAD的面积的最大值为,P(1,);(3)点Q的坐标为(0,)或(0,﹣9)
解:(1)∵抛物线y=ax2+bx+c与x轴交于A(﹣2,0)、B(6,0)两点,
∴设抛物线的解析式为y=a(x+2)(x﹣6),
∵D(4,3)在抛物线上,
∴3=a(4+2)×(4﹣6),解得a,
∴抛物线的解析式为y(x+2)(x﹣6)x2+x+3,
∵直线l经过A(﹣2,0)、D(4,3),
设直线l的解析式为y=kx+m(k≠0),
则,解得,,
∴直线l的解析式为yx+1;
(2)如图1中,过点P作轴交AD于点T.
设P(m, m2+m+3),则T(m,m+1).
∵S△PAD (xD﹣xA) PT=3PT,
∴PT的值最大值时,△PAD的面积最大,
∵PTm2+m+3m﹣1m2m+2(m﹣1)2,
∵0,抛物线开口向下,
∴m=1时,PT的值最大,最大值为,
此时△PAD的面积的最大值为,P(1,).
(3)如图2中,将线段AD绕点A逆时针旋转90°得到AT,
过作轴于 过作轴于
T(﹣5,6),
设DT交y轴于点Q,则∠ADQ=45°,
∵D(4,3),∴直线DT的解析式为yx,
∴Q(0,),作点T关于AD的对称点,
同理可得(1,﹣6),
则直线DT′的解析式为y=3x﹣9,
设DQ′交y轴于点Q′,则∠ADQ′=45°,
∴Q′(0,﹣9),
综上所述,满足条件的点Q的坐标为(0,)或(0,﹣9).
20.(1)yx2+x+4;顶点坐标为(1,);(2)点E的坐标为(3,);或(1,);(3)菱形的边长为
解:(1)∵抛物线的图象经过点A(﹣2,0),点B(4,0),
∴,
∴解得,
∴抛物线解析式为,
∵,
∴抛物线的顶点坐标为(1,);
(2)如图1,
①当点E位于直线CD下方时,过点E作EF⊥CD,垂足为F,设满足条件的点在抛物线上:
则,,,
根据题意,当时,,
即,
∴,
解得(舍去),,
∴;
②当点E'位于直线CD上方时,过点E'作E'F'⊥直线CD,垂足为F',设
则,,,
根据题意,当时,,
即,
∴,
解得(舍去),,
∴,
所以,点E的坐标为或;
(3)①CM为菱形的边,如图2,
在第一象限内取点P′,过点P′作轴,交BC于N′,过点P′作,交y轴于M′,
∴四边形CM′P′N′是平行四边形,
∵四边形CM′P′N′是菱形,
∴,
过点P′作轴,垂足为Q′,
∵,,
∴,
∴,设点,
在中,,,
∵,,
∴直线BC的解析式为,
∵轴,
∴,
∴,
∴,
解得:(舍)或,
菱形CM′P′N′的边长为;
②CM为菱形的对角线,如图3,
在第一象限内抛物线上取点P,过点P作,交y轴于点M,连接CP,过点M作,交BC于N,
∴四边形CPMN是平行四边形,连接PN交CM于点Q,
∵四边形CPMN是菱形,
∴,,
∵,
∴,
∴,
∴,
∴,
设点,
∴,,
∴
∴(舍),
∴此种情况不存在.
综上,菱形的边长为.
平行四边形及菱形的性质等,理解题意,作出相应图形结合这些知识点是解题关键.
21.(1);(2)P点坐标为(-3,-5);(3)F的坐标为(-4,-12).
解:(1)∵抛物线y=ax2+bx+c的图象与x轴交于A(2,0),B(﹣8,0)两点,
∴可设抛物线解析式为,
又∵抛物线的图像经过点C(0,-8),
∴,
∴,
∴抛物线解析式为;
(2)如图所示,连接BP,AP,CP,设BC于抛物线对称轴交于 ,
∵A(2,0)、B(-8,0)分别是抛物线与x轴的两个交点,
∴A、B关于抛物线对称轴对称,即关于直线对称,
∴PA=PB,
∴PA+PC=PB+PC,
∴要使PA+PC最小,即PB+PC最小,
∴当B、P、C三点共线时,PB+PC最小,即此时P点在的位置,
设直线BC的解析式为,
∴,
∴,
∴直线BC的解析式为,
当时,,
∴P点坐标为(-3,-5);
(3)如图所示,过点F作FN∥y轴,交BC于N,
设F的坐标为(t,),则N点坐标为(t,-t-8),
∴,
∴
,
∴当时,△BCF的面积最大,
∴F的坐标为(-4,-12).
试卷第1页,共3页
